集成学习-Adaboost

Adaboost 中文名叫自适应提升算法，是一种boosting算法。

boosting算法的基本思想

对于一个复杂任务来说，单个专家的决策过于片面，需要集合多个专家的决策得到最终的决策，通俗讲就是三个臭皮匠顶个诸葛亮。

对于给定的数据集，学习到一个较弱的分类器比学习到一个强分类器容易的多，boosting就是从弱学习器出发，反复学习，得到多个弱分类器，最后将这些弱分类器组合成强分类器。

boosting算法需要解决两个问题

每一轮如何改变训练样本的权重

如何将弱分类器组合成强分类器

adaboost是这样做的

1. 提高那些被前一轮弱分类器错误分类的样本的权值，而降低那些被正确分类样本的权值.，这样下个分类器就能专注于那些不好识别的样本，针对性的建立分类器。

2. 对于若分类器的组合，adaboost采取加权多数表决的方式，即加大分类错误率较小的弱分类器的权值，使其在表决中起较大作用，减小分类错误率较高的弱分类器的权值，使其在表决中起较小作用，

这可以理解为有些专家比较权威，他的意见要多采纳，有些只是不知名的专家，可以少采纳。

adaboost其实是一个加法模型，损失函数是指数损失函数，学习算法为前向分步算法的二分类学习方法。（其他学习算法如梯度下降）

加法模型

xgboost中其实也是加法模型，应该说boosting算法都是加法模型，而且还有很多算法也是加法模型，那什么是加法模型？

顾名思义，一个模型是由多个模型相加而得

那最终问题转化为基于加法模型的损失最小化，即

通常这是一个十分复杂的优化问题，想要一步到位非常困难，如用梯度下降，所以就有了前向分步算法。

前向分步算法

前向分步算法是一种优化算法，可以解决上面加法模型的问题。

大致思路是，从前向后，每一步学习一个基分类器，使得整体损失函数更小一点，从而逐步逼近全局最小值。

算法流程

解释一点： 新的学习器f_m是在上个学习器f_m-1的基础上学习的，也就是说在学习f_m时f_m-1已经确定，所以求L(y, f_m)的极小值就是求b(x;r)的极小值，即单个学习器的最小值。

实际上这和梯度下降的思路十分相似，每次减小一点，逼近一点，而且形式也一样 f_m=f_m-1+βb

adaboost算法流程

 

误差解释

1. 误差计算时除以了Σw，因为每轮迭代时，Σw是一个固定值，而且后面会说明其实它等于1，所以不用除这个。

2. 误差计算时，分类正确为0，其权重被忽略，分类错误为1，其权重累加，所以是I(G!=y)

分类器权重解释

权重更新解释

组合分类器解释

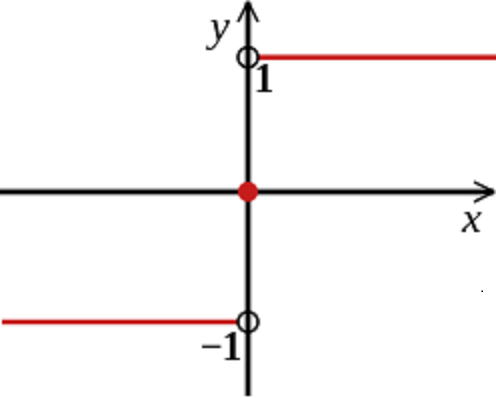
sign函数只能取1和-1，故adaboost为二分类。

当然可以通过修改实现多分类。

adaboost有很多种算法，但都大同小异，而且adaboost可以做回归，思路也是大同小异，具体请百度

adaboost进阶

正则化

adaboost每个学习器都是弱学习器，为什么还要正则化？其实不是正则化基学习器

fm=fm-1+αb(x,r)，这是加法模型，α为基学习器的系数，可以理解为权重，

正则化是对加法模型增加一个学习率v，即fm=fm-1+vαb(x,r)，这种方法适合于很多集成学习。

基分类器随机化

像随机森林一样，随机选特征，随机选样本

总结

理论上来讲，adaboost的弱学习器可以是任何模型，但用的最多的是决策树和神经网络，决策树是cart树

优点：精度高，不容易过拟合

缺点：对异常值敏感，因为异常值可能获得较大权重，最终影响整个模型

参考资料：

https://www.cnblogs.com/liuwu265/p/4693113.html?ptvd

https://zhuanlan.zhihu.com/p/59751960

https://zhuanlan.zhihu.com/p/42915999

https://blog.csdn.net/hahaha_2017/article/details/79852363

https://blog.csdn.net/guyuealian/article/details/70995333　　原理-实例-代码（简明易懂）