POJ 3233Matrix Power Series

妈妈呀....这简直是目前死得最惨的一次。

贴题目：

http://poj.org/problem?id=3233

Matrix Power Series

Time Limit: 3000MS	Memory Limit: 131072K
Total Submissions: 19128	Accepted: 8068

Description

Given a n × n matrix A and a positive integer k, find the sum S = A + A² + A³ + … + A^k.

Input

The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 10⁹) and m (m < 10⁴). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.

Output

Output the elements of S modulo m in the same way as A is given.

Sample Input

2 2 4
0 1
1 1

Sample Output

1 2
2 3

Source

POJ Monthly--2007.06.03, Huang, Jinsong

首先我在克服重重困难后解决了矩阵的问题（工商管理第一学期还不学线性代数2333333）

 

原来的代码：

 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <cmath>
 #include <cstdlib>

 #define rep(i,a,n) for(int i = a;i <= n;i++)
 #define per(i,n,a) for(int i = n;i>=a;i--)
 #define pb push_back
 #define VI vector<int>
 #define QI queue<int>
 #define logM(N) log10(N)/log10(M)
 #define eps 1e-8

 typedef long long ll;

 using namespace std;

 int n,m,k;

 struct node{
     ll mat[][];
 }h,sum;

 node operator * (const node &a,const node &b){
         node ret;
         memset(ret.mat,,sizeof(ret.mat));
         rep(i,,n-){
             rep(j,,n-){
                 rep(k,,n-){
                     ret.mat[i][j] += (a.mat[i][k] * b.mat[k][j])%m;
                     //cout<<"a.mat["<<i<<"]["<<k<<"]="<<a.mat[i][k]<<" b.mat["<<k<<"]["<<j<<"]="<<b.mat[k][j]<<endl;
                     //cout<<"i = "<<i<<" j = "<<j<<" ret.mat["<<i<<"]["<<j<<"]="<<ret.mat[i][j]<<endl;
                 }
                 if(ret.mat[i][j] > m) ret.mat[i][j] %= m;
             }
         }
         return ret;
 }

 node operator + (const node &a,const node &b){
     node ret;
     memset(ret.mat,,sizeof(ret.mat));
     rep(i,,n-){
         rep(j,,n-){
             ret.mat[i][j] = a.mat[i][j] + b.mat[i][j];
             if(ret.mat[i][j] > m) ret.mat[i][j] %= m;
         }
     }
     return ret;
 }

 void pow_mod(int x){
     x--;
     node a,b;
     a = b = h;
     while(x){
         if(x&) a = a * b;
         b = b * b;
         x >>= ;
     }
     /*cout<<"========"<<endl;
     rep(i,0,n-1){
         rep(j,0,n-1){
             printf("%d ",a.mat[i][j]);
         }puts("");
     }
     cout<<"========"<<endl;
     */
     sum = sum + a;
 }

 int main()
 {
 #ifndef ONLINE_JUDGE
     freopen("in.txt","r",stdin);
     //freopen("out.txt","w",stdout);
 #endif
     while(~scanf("%d%d%d",&n,&k,&m)){
         memset(sum.mat,,sizeof(sum.mat));
         rep(i,,n-){
             rep(j,,n-){
                 scanf("%I64d",&h.mat[i][j]);
             }
         }
         rep(i,,k){
             pow_mod(i);
         }
         rep(i,,n-){
             rep(j,,n-){
                 if(j != n-){
                     printf("%I64d ",sum.mat[i][j]%m);
                 }
                 else{
                     printf("%I64d\n",sum.mat[i][j]%m);
                 }
             }
         }
     }
     return ;
 }

其实在这边代码之前已经错了十多遍了。看了学姐的代码，也仔细审视了自己的代码。总的小小的零零碎碎的错误找出不少。

现在这个代码的情况就是TLE

估计里面的测试数据很大，还得优化一下，那么还可以优化的地方就是求sum这个地方。

原理直接盗用学姐给的图片：

优化之后的代码：

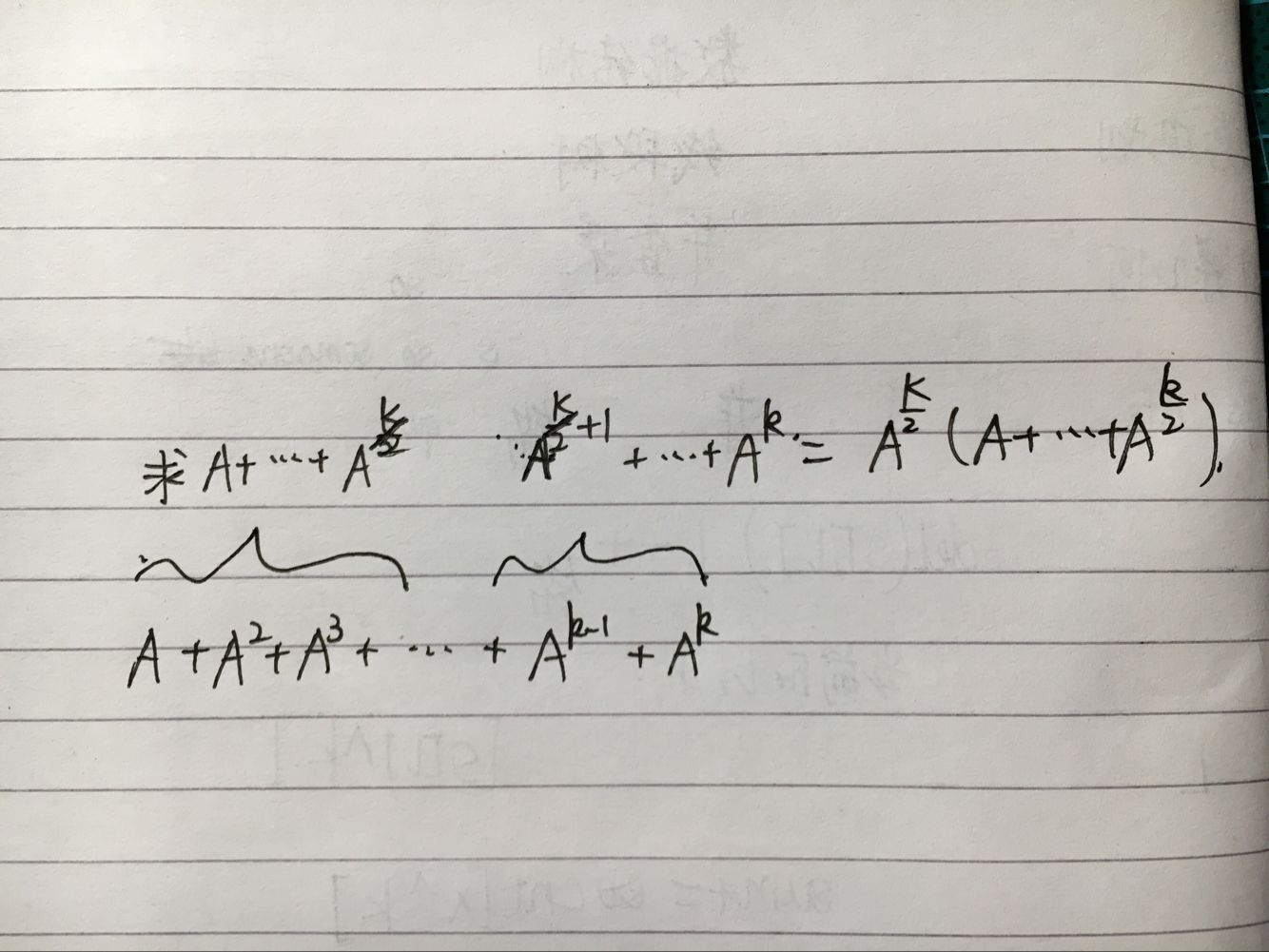
 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <cmath>
 #include <cstdlib>

 #define rep(i,a,n) for(int i = a;i <= n;i++)
 #define per(i,n,a) for(int i = n;i>=a;i--)
 #define pb push_back
 #define VI vector<int>
 #define QI queue<int>
 #define logM(N) log10(N)/log10(M)
 #define eps 1e-8

 typedef long long ll;

 using namespace std;

 int n,m,k;

 struct node{
     ll mat[][];
 }h,sum;

 node operator * (const node &a,const node &b){
         node ret;
         memset(ret.mat,,sizeof(ret.mat));
         rep(i,,n-){
             rep(j,,n-){
                 rep(k,,n-){
                     ret.mat[i][j] += (a.mat[i][k] * b.mat[k][j])%m;
                 }
                 if(ret.mat[i][j] > m) ret.mat[i][j] %= m;
             }
         }
         return ret;
 }

 node operator + (const node &a,const node &b){
     node ret;
     memset(ret.mat,,sizeof(ret.mat));
     rep(i,,n-){
         rep(j,,n-){
             ret.mat[i][j] = a.mat[i][j] + b.mat[i][j];
             if(ret.mat[i][j] > m) ret.mat[i][j] %= m;
         }
     }
     return ret;
 }

 node pow_mod(int x){
     x--;
     node a,b;
     a = b = h;
     while(x){
         if(x&) a = a * b;
         b = b * b;
         x >>= ;
     }
     return a;
 }

 node work(int p){
     if(p == ) return h;
     node ret = work(p>>);
     ret = ret + ret * pow_mod(p>>);
     if(p&) ret = ret + pow_mod(p);
     return ret;
 }

 int main()
 {
 #ifndef ONLINE_JUDGE
     //freopen("in.txt","r",stdin);
     //freopen("out.txt","w",stdout);
 #endif
     while(~scanf("%d%d%d",&n,&k,&m)){
         memset(sum.mat,,sizeof(sum.mat));
         rep(i,,n-){
             rep(j,,n-){
                 scanf("%I64d",&h.mat[i][j]);
             }
         }
         sum = work(k);
         rep(i,,n-){
             rep(j,,n-){
                 if(j != n-){
                     printf("%I64d ",sum.mat[i][j]%m);
                 }
                 else{
                     printf("%I64d\n",sum.mat[i][j]%m);
                 }
             }
         }
     }
     return ;
 }