5.聚类算法k-means

聚类与分类的区别在于，是在没有给定划分类别的情况下，更具数据相似度进行样本分组的一种办法，是一种非监督的学习算法，聚类的输入时一组未被标记的样本，聚类更具数据自身的距离或者相似度将其划分为若干组，划分的原则是组内距离最小化，而组间（外部）距离最大化。

聚类中的k-means算法

1. k-means工作过程：

　　下述图片均来自网络

　　

　　

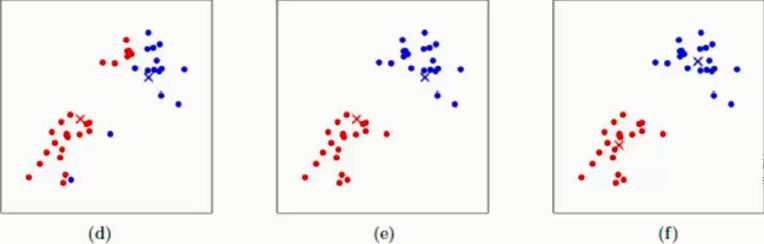
　　（a）表示两类点

　　（b）表示随机选取两个点作为中心点

　　（c）表示测点上述两类点到我们在（b）中随机选定的红色×和蓝色×之间的距离，离哪个中心点近就归为相应的类别，在（c）中我们就已经将上述两类点进行分为两类

　　（d）在上述c的基础上利用红色圆点重新计算红色类的中心点，蓝色同理就会得到如（d）图所示的红×与蓝×，此时中心点即得到了一次更新

　　（e）以（d）中确定的中心点再次计算所有样本点到（d）中心点的距离，离哪个中性点近就归为相应类别即得到了（e）中的分类效果

　　（f）和（d）同样的方式再次利用新的类别的样本点更新中心点

　　如上述步骤：不断迭代直至聚类的中心点不在发生变化，或者每个样本到对应聚类中心的距离之和不再有很大变化即可停止，聚类任务结束

　　

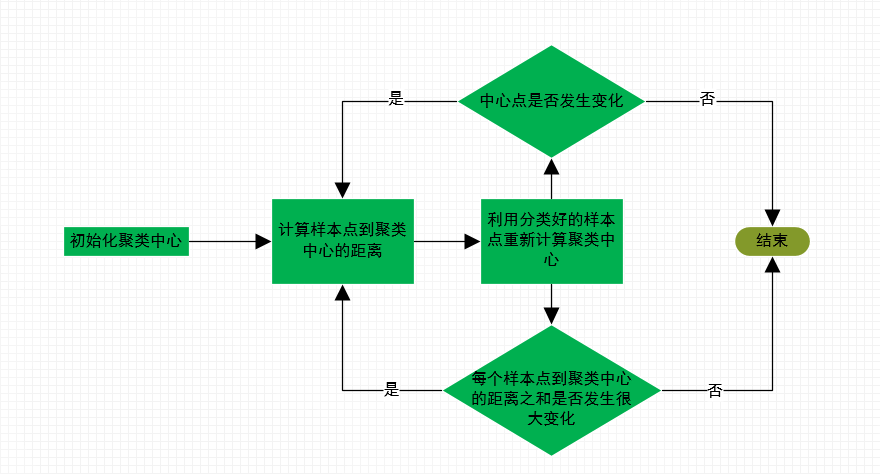
2. k-means算法注意点

　　2.1 我们在初始化聚类中心时，有如下两种办法：

　　（1）随机初始化k个和样本点维度相同的向量

　　（2）随机在选择k个不同的样本点作为初始的聚类中心

　　我们所选定的初始聚类中心会对我们模型最终的聚类结果有一定的影响，我们可以通过下述方法，将初始聚类中心对聚类结果的影响程度最小

　　（1）多次初始化，最终参考多次运行的结果取平均

　　（2）在样本点中选择初始聚类中心时，使得所选择的聚类中心之间离的尽量远

　　2.2 在面对一些问题的时候，我们并不知道它们的类别，所以k值的确定至关重要

　　　　

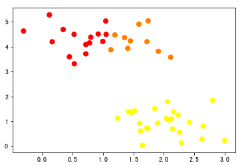
　　如上图，可以知道k值选择不合适，聚类的结果往往是没有意义的，故我们要选择不同的k值进行测试

　　2.3 k-means聚类的局限性

　　如下图所示，此类样本点，k-means无法完成准确聚类，此类样本分布规律，我们可以用DBSCAN算法（即基于高密度连接区域）进行聚类

　　

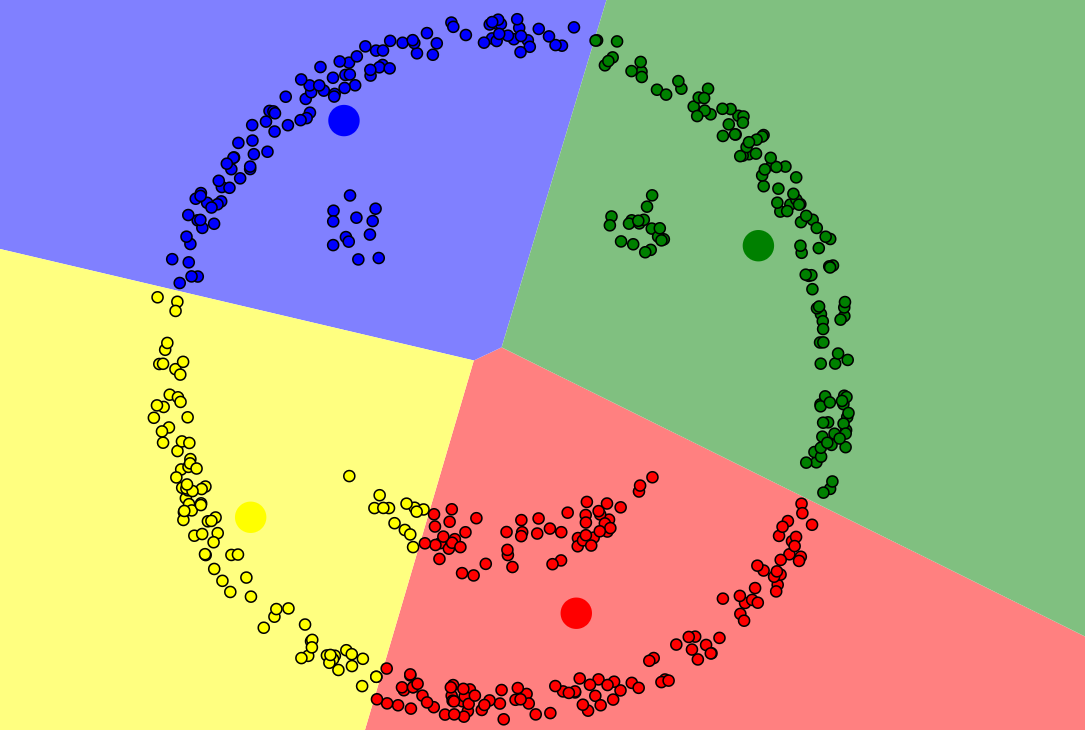
3. k-means原理的python代码实现过程如下：

import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets.samples_generator import make_blobs
'''
利用sklearn随机生成数据，这里注意利用make_blobs生成的原本为分类问题，在此处我们忽略标记y，只考虑X
即为一个聚类问题
'''
X,y = make_blobs(n_samples=50,centers=2,random_state=0,cluster_std=0.5)
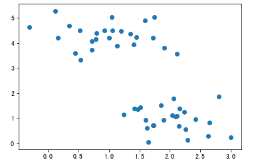
# 通过观察散点图，上下各为一个类别
plt.scatter(X[:,0],X[:,1])

# 聚类前样本点的散点图

# 测量欧式距离，对样本点依据中心点分类
def sample_classify(sample_data,centerPoint):
    '''
    sample_classify:计算所有样本点到中心点的距离，并对样本点进行分类
    参数：sample_data:某一样本点数据
         centerpoint:k-means算法中心点
    '''
    # 计算样本数据到第一个中心点的欧氏距离
    mindist = np.linalg.norm(sample_data-centerPoint[0,:-1])
    # n 表示中心点的个数
    n = centerPoint.shape[0]
    # lagel表示中心点所代表的类别
    label = centerPoint[0,-1]
    for i in range(1,n):
        # 计算样本点到剩余中心点的欧式距离
        dist = np.linalg.norm(sample_data-centerPoint[i,:-1])
        # 比较剩余中心点到样本距离与第一个中心点到样本点的距离
        if dist < mindist:
            mindist = dist
            label = centerPoint[i,-1]
    # 返回类别
    return label    

# 定义模型停止策略
def interation_stop(iterations,centerPoint,oldcenterPoint,maxIt):
    '''
    interation_stop:定义停止策略，1.迭代次数到达设定值，2.中心点不在移动
    参数：iterations:迭代次数
         centerPoint:本次中心点
         oldcenterPoint:上次中心点
         maxIt:预设的迭代次数
    '''
    # 当迭代次数大于或者等于我们预设的迭代次数时停止
    if iterations >= maxIt:
        print('-------------')
        return True
    # 判断两次中心点是否相等
    return np.array_equal(oldcenterPoint, centerPoint)  

# 更新中心点
def get_centerPoint(dataSet,k):
    '''
    get_centerPoint:更新中心点，当数据被分好类以后，根据已经分好类的数据重新计算中心点，然后再次重复以上的步骤对数据进行
    参数：dataSet:已经经过聚类的数据集
         k:类别个数
    '''
    #初始化一个k行，数据维度列的一个array
    result = np.zeros((k,dataSet.shape[1]))
    for i in range(1,k+1):
        # 找出同一类别的数据
        oneCluster = dataSet[dataSet[:,-1]==i,:-1]
        # 计算同一类别数据各个维度的均值，即计算出新的中心点
        result[i-1,:-1] = np.mean(oneCluster,axis=0)
        # 给定类别
        result[i-1,-1] = i
    return result    

def main():
    #orig_data = np.array([[1,1],[2,1],[4,3],[5,4]])
    # 初始化数据
    orig_data = X
    # 将数据形式又array转化成matrix
    data = np.mat(orig_data)
    # 初始化k值即类别
    k = 2
    # num表示样本个数，dim表示每一个样本的维度
    num,dim = data.shape
    # 初始化一个新的数组用于存放原数据与对应类别
    dataSet = np.zeros((num,dim+1))
    # 将原始数据填入新的数据
    dataSet[:,:-1] = data
    # 随机选取的中心点
    centerPoint = dataSet[np.random.randint(num,size=k),:]
    centerPoint[:,-1] = range(1,k+1)
    oldcenterPoint = None
    iterations = 0
    # 指定迭代次数
    maxIt = 1000
    # 停止策略未false时循环
    while not interation_stop(iterations,centerPoint,oldcenterPoint,maxIt):
        for i in range(num):
            # 取出样本点
            sample_data = dataSet[i,:-1]
            # 利用之前定义好的函数计算每一个样本点到中心点距离，并对样本点进行分类
            dataSet[i,-1] = sample_classify(sample_data,centerPoint)
        # 记录此次计算的中心点
        oldcenterPoint = np.copy(centerPoint)
        # 更新中心点
        centerPoint = get_centerPoint(dataSet,k)
        # 记录迭代次数
        iterations += 1
    #print(dataSet)
    # y表示已经确定好的类别
    y = dataSet[:,2]
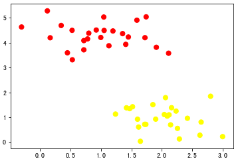
    # 画出散点图，观察聚类效果
    plt.scatter(dataSet[:,0],dataSet[:,1],c=y,s=50,cmap='autumn')

if __name__ == '__main__':
    main()

# 聚类后样本点的散点图