vjudge I - Vladik and fractions 一道小学生的提。
原题链接:https://vjudge.net/contest/331993#problem/I
Vladik and Chloe decided to determine who of them is better at math. Vladik claimed that for any positive integer n he can represent fraction as a sum of three distinct positive fractions in form
.
Help Vladik with that, i.e for a given n find three distinct positive integers x, y and z such that . Because Chloe can't check Vladik's answer if the numbers are large, he asks you to print numbers not exceeding 109.
If there is no such answer, print -1.
Input
The single line contains single integer n (1 ≤ n ≤ 104).
Output
If the answer exists, print 3 distinct numbers x, y and z (1 ≤ x, y, z ≤ 109, x ≠ y, x ≠ z, y ≠ z). Otherwise print -1.
If there are multiple answers, print any of them.
Examples
3
2 7 42
7
7 8 56 简单来说,就是对于给定的n,构建一组x,y,z,使得1/x + 1/y +1/z =2/ n 然后 当n=1的时候 输出-1
#include<bits/stdc++.h>
using namespace std;
int main() {
int n;
cin>>n;
if(n==) cout<<"-1"<<endl;
else cout<<n<<endl<<n+<<endl<<n*(n+);
return ;
}
其实, 可以看作,
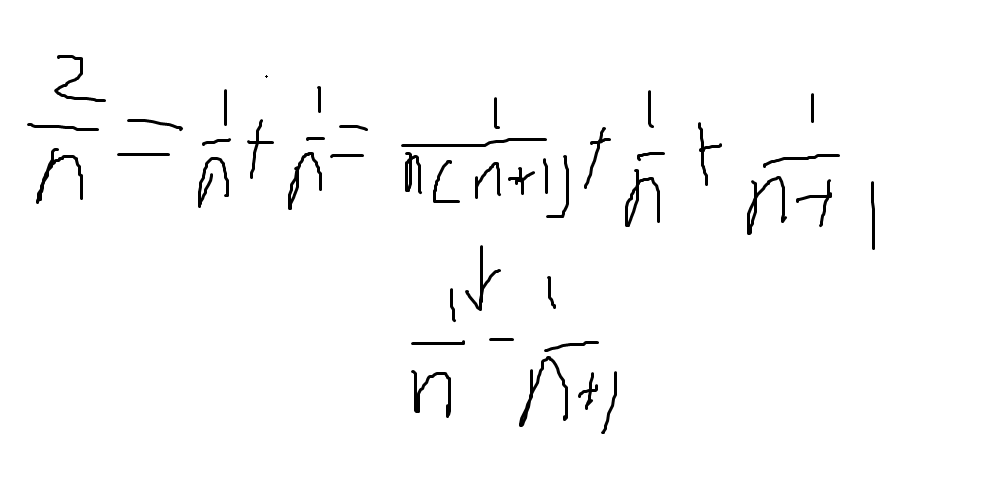
vjudge I - Vladik and fractions 一道小学生的提。的更多相关文章
- Codeforces Round #384 (Div. 2) C. Vladik and fractions 构造题
C. Vladik and fractions 题目链接 http://codeforces.com/contest/743/problem/C 题面 Vladik and Chloe decided ...
- Codeforces 743C - Vladik and fractions (构造)
Codeforces Round #384 (Div. 2) 题目链接:Vladik and fractions Vladik and Chloe decided to determine who o ...
- Codeforces Round #384 (Div. 2) C. Vladik and fractions(构造题)
传送门 Description Vladik and Chloe decided to determine who of them is better at math. Vladik claimed ...
- 【44.64%】【codeforces 743C】Vladik and fractions
time limit per test1 second memory limit per test256 megabytes inputstandard input outputstandard ou ...
- CodeForces 743C Vladik and fractions (数论)
题意:给定n,求三个不同的数满足,2/n = 1/x + 1/y + 1/z. 析:首先1是没有解的,然后其他解都可以这样来表示 1/n, 1/(n+1), 1/(n*(n+1)),这三个解. 代码如 ...
- 数学【CF743C】Vladik and fractions
Description 请找出一组合法的解使得\(\frac {1}{x} + \frac{1}{y} + \frac {1}{z} = \frac {2}{n}\)成立 其中\(x,y,z\)为正整 ...
- CF C. Vladik and fractions——构造题
题目 构造一组 $x, y, z$,使得对于给定的 $n$,满足 $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = \frac{2}{n}$. 分析: 样例二已 ...
- [codeforces743C]:Vladik and fractions(数学)
题目传送门 题目描述 请找出一组合法解使得$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{2}{n}$成立. 其中$x,y,z$为正整数且互不相同. 输入格式 一 ...
- CF2.C
C. Vladik and fractions time limit per test 1 second memory limit per test 256 megabytes input stand ...
随机推荐
- 【GET TIPS】Chrome所见即所得的截图技巧
精简的前言: 对,我就是想说下事情的来龙去脉.您要不想听,就把耳朵捂起来23333. 想截个新冠肺炎病毒,全国确诊人数今日增长的图,以确定非湖北地区不再明显增长. 但由于网页需要的内容分布在两页,需要 ...
- NCE L3
单词 课文
- 聊聊GIS中的坐标系|再版 识别各种数据的坐标系及代码中的坐标系
本篇讲讲在GIS桌面软件和实际数据中,以及各路GIS有关API的编程中,如何寻找坐标系信息.惯例: 本文约2000字,建议阅读时间10分钟. 作者:博客园/B站/知乎/csdn/小专栏 @秋意正寒 版 ...
- JAVA系统架构高并发解决方案 分布式缓存 分布式事务解决方案
JAVA系统架构高并发解决方案 分布式缓存 分布式事务解决方案
- Docker下Jenkins的安装部署、更新
一.下载Jenkins镜像 docker pull jenkins/jenkins 二.创建挂载文件 mkdir /srv/jenkins chown -R : /srv/jenkins 三.启动Do ...
- C#实现的一些常见时间格式
string aa = DateTime.Now.ToShortDateString();//"2019/9/23" string bb = DateTime.Now.ToShor ...
- 解决visual studio 2013编译过程中存在的无法打开kernel.lib问题
1. 出现此类问题的原因 由于原visual studio文件中的安装中出现问题,所以原有的SDK(soft development kits)文件出现缺失: 2. 解决方法1 重新下载SDK工具,安 ...
- 《手把手教你构建自己的 Linux 系统》学习笔记(6)
目录 /dev 目录是干什么的? /proc 和 /sys 目录是干什么的? udev 这个软件是干什么用的? 目录映射是临时性的,还是永久性的? 命令行里大括号 "{}" 的作用 ...
- 剑指offer-面试题56_2-数组中唯一只出现一次的数字-位运算
/* 题目: 数组中除一个数字只出现一次外,其余数字都出现3次. */ /* 思路: 位运算. */ #include<iostream> #include<cstring> ...
- 【python基础语法】第2天作业练习题
""" 1.用户输入一个数值,请判断用户输入的是否为偶数?是偶数输出True,不是输出False(提示:input输入的不管是什么,都会被转换成字符串,自己扩展,想办法将 ...
