数据结构（C语言版）-第7章 查找

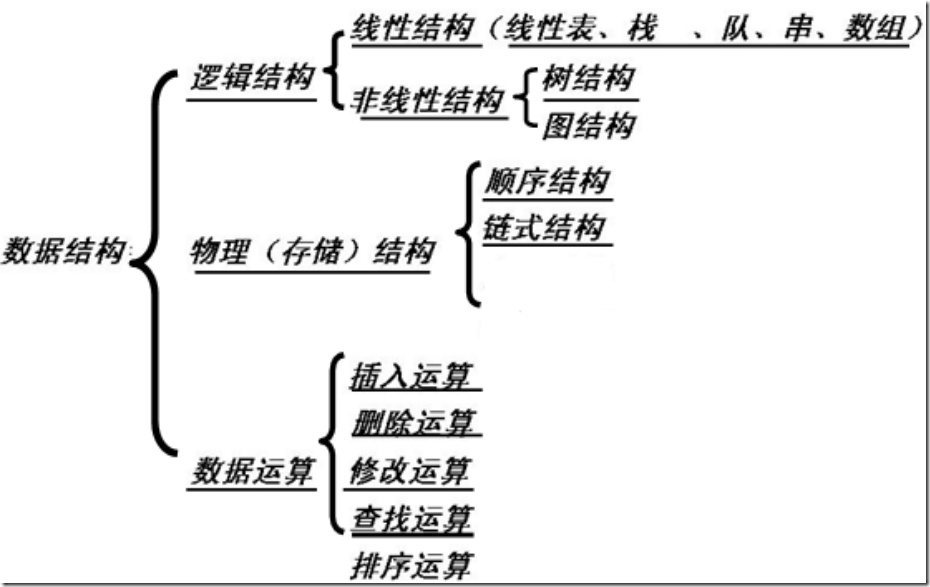
7.1　查找的基本概念

查找表:
    由同一类型的数据元素（或记录）构成的集合
静态查找表：
    查找的同时对查找表不做修改操作（如插入和删除）
动态查找表：
    查找的同时对查找表具有修改操作
关键字
    记录中某个数据项的值，可用来识别一个记录
主关键字：
    唯一标识数据元素
次关键字：
    可以标识若干个数据元素

查找算法的评价指标

关键字的平均比较次数，也称平均搜索长度ASL(Average Search Length)

n：记录的个数
pi：查找第i个记录的概率 ( 通常认为pi =1/n )
ci：找到第i个记录所需的比较次数

7.2　线性表的查找

一、顺序查找（线性查找）

应用范围：
　　顺序表或线性链表表示的静态查找表
　　表内元素之间无序

顺序表的表示

typedef struct {
          ElemType   *R; //表基址
          int          length;     //表长
}SSTable;

第2章在顺序表L中查找值为e的数据元素

int LocateELem(SqList L,ElemType e)
{  for (i=;i< L.length;i++)
      if (L.elem[i]==e) return i+;
  return ;}

改进：把待查关键字key存入表头（“哨兵”），从后向前逐个比较，可免去查找过程中每一步都要检测是否查找完毕，加快速度。

int Search_Seq( SSTable  ST , KeyType  key ){
   //若成功返回其位置信息，否则返回0
  ST.R[].key =key;
for( i=ST.length; ST.R[ i ].key!=key;  - - i  );
//不用for(i=n; i>0; - -i) 或 for(i=1; i<=n; i++)
   return i;
}

顺序查找的性能分析:

空间复杂度：一个辅助空间。
时间复杂度：
1) 查找成功时的平均查找长度
  设表中各记录查找概率相等
    ASLs(n)=(1+2+ ... +n)/n =(n+1)/2
2)查找不成功时的平均查找长度    ASLf =n+1

顺序查找算法有特点:

算法简单，对表结构无任何要求（顺序和链式）
n很大时查找效率较低

改进措施：非等概率查找时，可按照查找概率进行排序。

二、折半查找（二分或对分查找）

若k==R[mid].key，查找成功
若k<R[mid].key，则high=mid-1
若k>R[mid].key，则low=mid+1

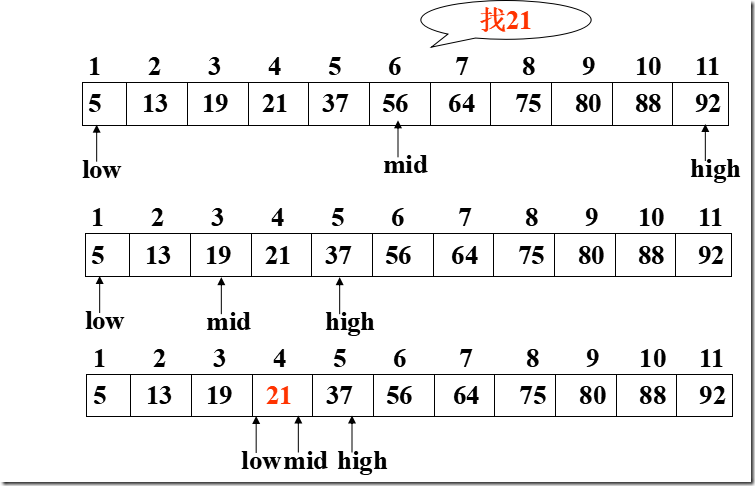
设表长为n，low、high和mid分别指向待查元素所在区间的上界、下界和中点,k为给定值
初始时，令low=1,high=n,mid=(low+high)/2
让k与mid指向的记录比较
若k==R[mid].key，查找成功
若k<R[mid].key，则high=mid-1
若k>R[mid].key，则low=mid+1
重复上述操作，直至low>high时，查找失败

int Search_Bin(SSTable ST,KeyType key){
//若找到，则函数值为该元素在表中的位置，否则为0
    low=;high=ST.length;                         while(low<=high){
        mid=(low+high)/;
        if(key==ST.R[mid].key) return mid;
        else if(key<ST.R[mid].key) high=mid-;//前一子表查找
        else low=mid+;                               //后一子表查找
    }                                        return ;        //表中不存在待查元素
}

折半查找的性能分析:

查找过程：每次将待查记录所在区间缩小一半，比顺序查找效率高,时间复杂度O(log2 n)

适用条件：采用顺序存储结构的有序表，不宜用于链式结构

三、分块查找

分块有序，即分成若干子表，要求每个子表中的数值都比后一块中数值小（但子表内部未必有序）。
然后将各子表中的最大关键字构成一个索引表，表中还要包含每个子表的起始地址（即头指针）。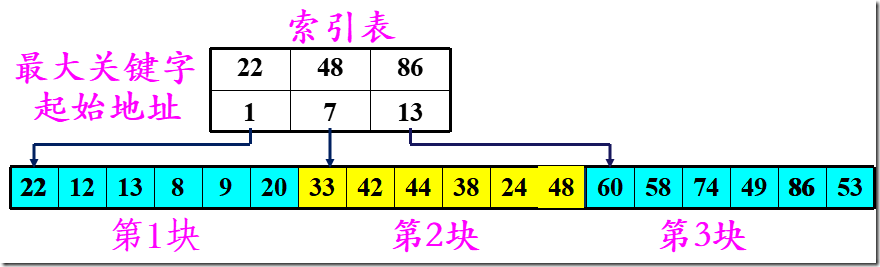

① 对索引表使用折半查找法（因为索引表是有序表）；
② 确定了待查关键字所在的子表后，在子表内采用顺序查找法（因为各子表内部是无序表）；

分块查找性能分析:

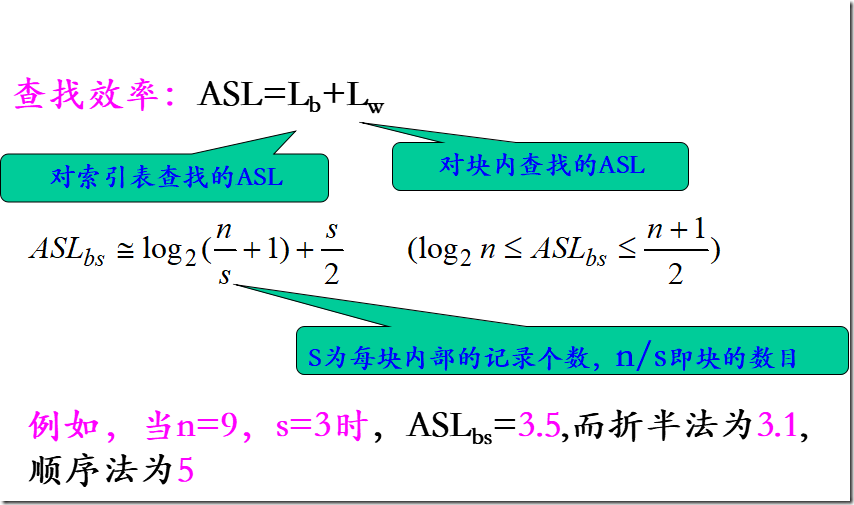
优点：插入和删除比较容易，无需进行大量移动。
缺点：要增加一个索引表的存储空间并对初始索引表进行排序运算。
适用情况：如果线性表既要快速查找又经常动态变化，则可采用分块查找。

7.3　树表的查找

二叉排序树
平衡二叉树
B-树
B+树
键树

二叉排序树:

二叉排序树或是空树，或是满足如下性质的二叉树：
(1)若其左子树非空，则左子树上所有结点的值均小于根结点的值；
(2)若其右子树非空，则右子树上所有结点的值均大于等于根结点的值；
(3)其左右子树本身又各是一棵二叉排序树

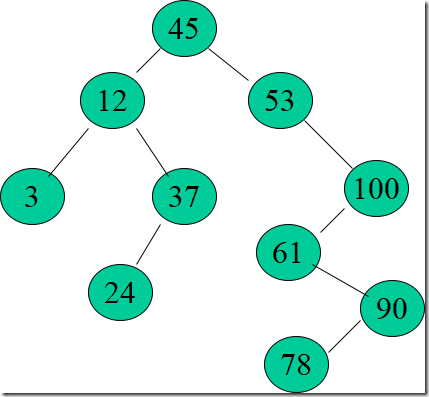
中序遍历二叉排序树后的结果有什么规律？

得到一个关键字的递增有序序列

二叉排序树的操作－查找

（1）若二叉排序树为空，则查找失败，返回空指针。
（2）若二叉排序树非空，将给定值key与根结点的关键字T->data.key进行比较：
① 若key等于T->data.key，则查找成功，返回根结点地址；
② 若key小于T->data.key，则进一步查找左子树；
③ 若key大于T->data.key，则进一步查找右子树。

BSTree SearchBST(BSTree T,KeyType key) {
   if((!T) || key==T->data.key) return T;
   else if (key<T->data.key)  return SearchBST(T->lchild,key);    //在左子树中继续查找
   else return SearchBST(T->rchild,key);                       //在右子树中继续查找
} // SearchBST

二叉排序树的操作－插入

若二叉排序树为空，则插入结点应为根结点
否则，继续在其左、右子树上查找
树中已有，不再插入
树中没有，查找直至某个叶子结点的左子树或右子树为空为止，则插入结点应为该叶子结点的左孩子或右孩子

插入的元素一定在叶结点上

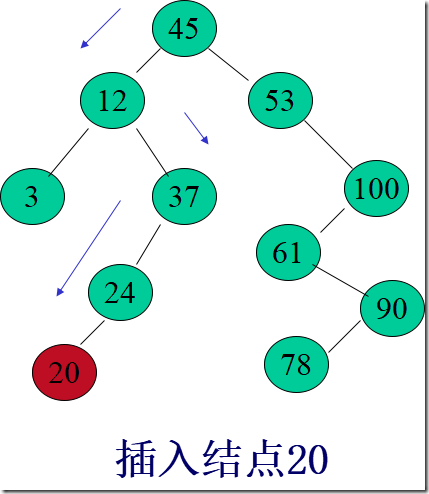
二叉排序树的操作－生成

从空树出发，经过一系列的查找、插入操作之后，可生成一棵二叉排序树

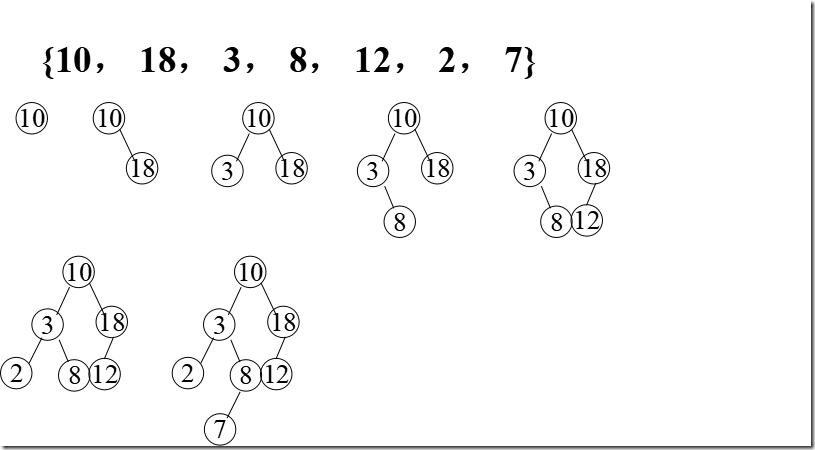
不同插入次序的序列生成不同形态的二叉排序树

二叉排序树的操作－删除

将因删除结点而断开的二叉链表重新链接起来
防止重新链接后树的高度增加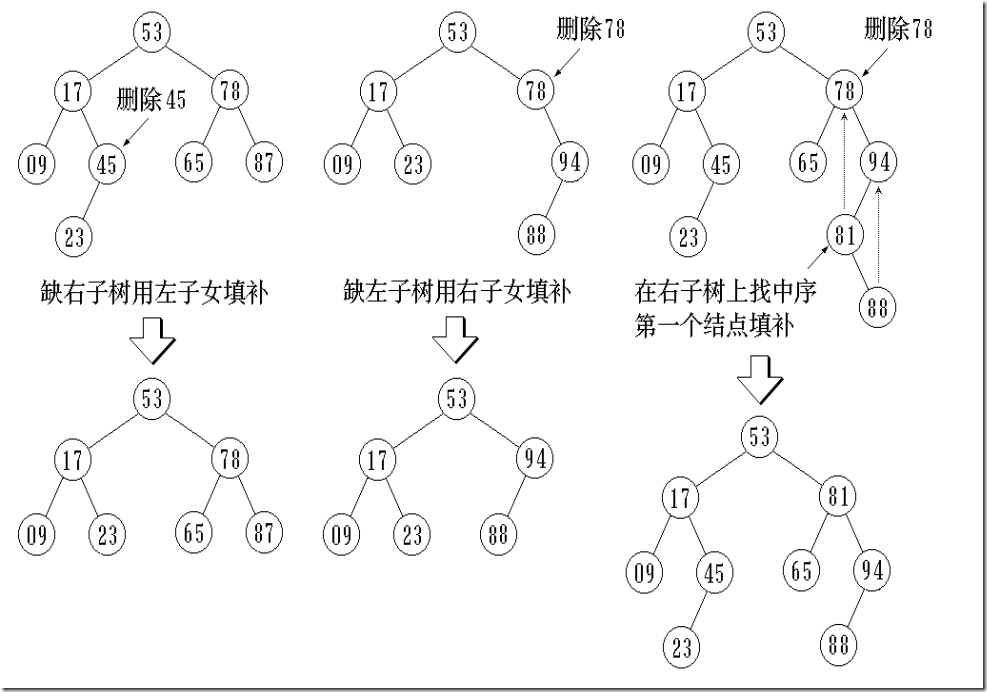

查找的性能分析:

平均查找长度和二叉树的形态有关，即，
最好：log2n（形态匀称，与二分查找的判定树相似）
最坏:  （n+1)/2（单支树）

平衡二叉树

左、右子树是平衡二叉树；
所有结点的左、右子树深度之差的绝对值≤ 1

平衡因子:该结点左子树与右子树的高度差

任一结点的平衡因子只能取：-1、0 或 1；如果树中任意一个结点的平衡因子的绝对值大于1，则这棵二叉树就失去平衡，不再是AVL树；

对于一棵有n个结点的AVL树，其高度保持在O(log2n)数量级，ASL也保持在O(log2n)量级。

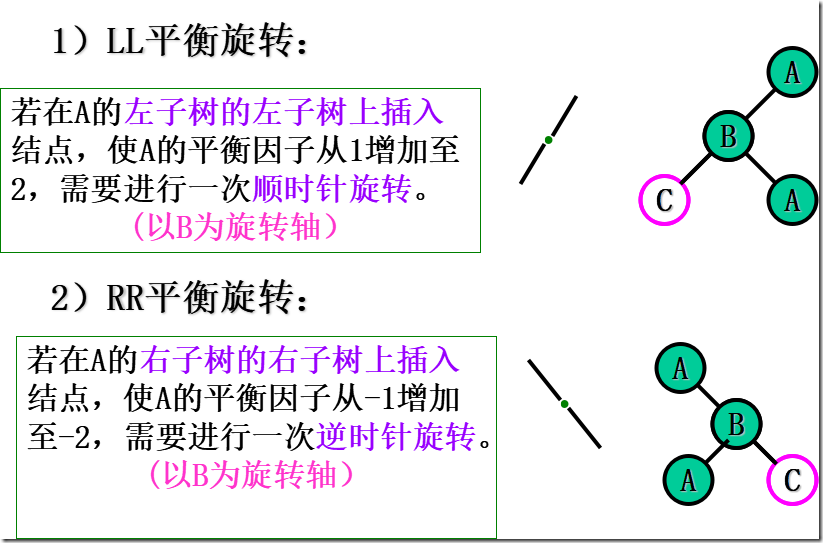
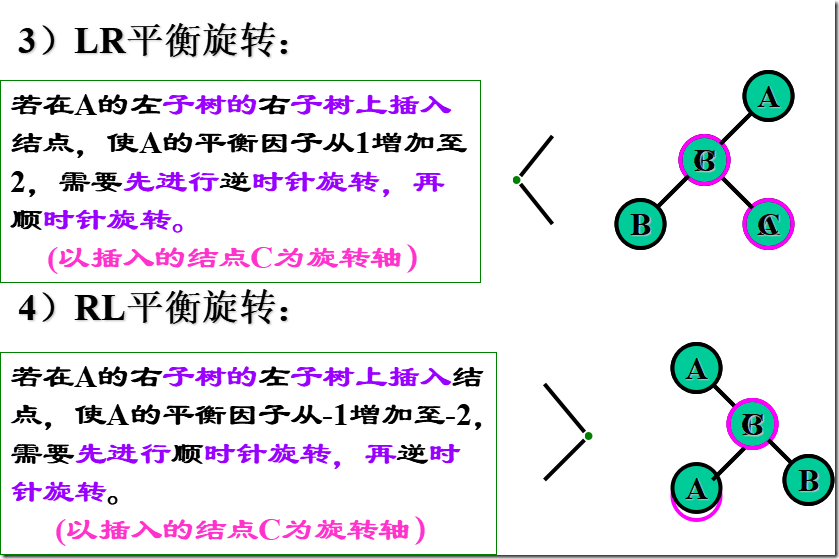
如果在一棵AVL树中插入一个新结点，就有可能造成失衡，此时必须重新调整树的结构，使之恢复平衡。我们称调整平衡过程为平衡旋转。

7.4　哈希表的查找

基本思想：记录的存储位置与关键字之间存在对应关系，Loc(i)=H(keyi)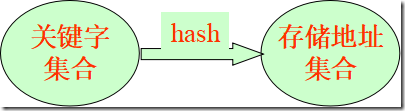

优点：查找速度极快O(1),查找效率与元素个数n无关

哈希方法(杂凑法)
选取某个函数，依该函数按关键字计算元素的存储位置，并按此存放；
查找时，由同一个函数对给定值k计算地址，将k与地址单元中元素关键码进行比，确定查找是否成功。

哈希函数(杂凑函数)：哈希方法中使用的转换函数

冲 突：不同的关键码映射到同一个哈希地址    key1key2，但H(key1)=H(key2)

同义词：具有相同函数值的两个关键字

如何减少冲突

哈希函数的构造方法

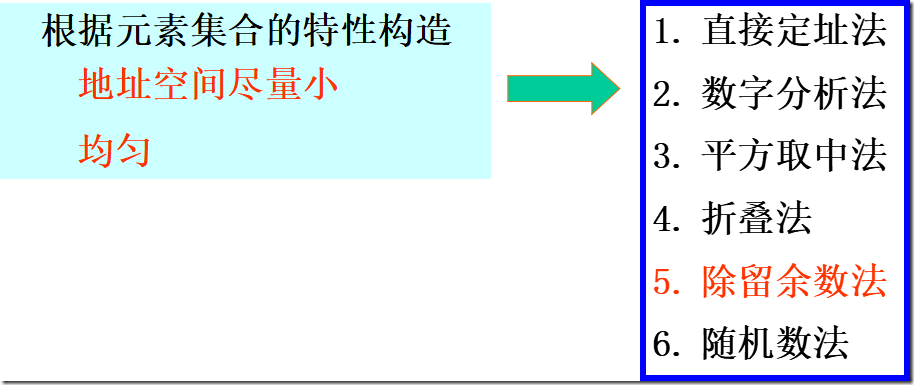
1. 直接定址法

Hash(key) = a·key + b    (a、b为常数)

优点：以关键码key的某个线性函数值为哈希地址，不会产生冲突。

缺点：要占用连续地址空间，空间效率低。

2. 数字分析法

3.  平方取中法

4. 折叠法

5. 除留余数法

Hash(key)=key  mod  p    (p是一个整数)

关键：如何选取合适的p？
技巧：设表长为m，取p≤m且为质数

6. 随机数法

处理冲突的方法

1.开放定址法（开地址法）   2.链地址法

1.开放定址法（开地址法）

基本思想：有冲突时就去寻找下一个空的哈希地址，只要哈希表足够大，空的哈希地址总能找到，并将数据元素存入。

线性探测法

Hi=(Hash(key)+di) mod m       ( 1≤i < m )
  其中：m为哈希表长度
     di 为增量序列 1，2，…m-1，且di=i

一旦冲突，就找下一个空地址存入

优点：只要哈希表未被填满，保证能找到一个空地址单元存放有冲突的元素。
缺点：可能使第i个哈希地址的同义词存入第i+1个地址，这样本应存入第i+1个哈希地址的元素变成了第i+2个哈希地址的同义词，……，产生“聚集”现象，降低查找效率。

解决方案：二次探测法

伪随机探测法

Hi=(Hash(key)+di) mod m       ( 1≤i < m )
  其中：m为哈希表长度
     di 为随机数

2.链地址法(拉链法）

基本思想：相同哈希地址的记录链成一单链表，m个哈希地址就设m个单链表，然后用用一个数组将m个单链表的表头指针存储起来，形成一个动态的结构

step1 取数据元素的关键字key，计算其哈希函数值（地址）。若该地址对应的链表为空，则将该元素插入此链表；否则执行step2解决冲突。
step2 根据选择的冲突处理方法，计算关键字key的下一个存储地址。若该地址对应的链表为不为空，则利用链表的前插法或后插法将该元素插入此链表。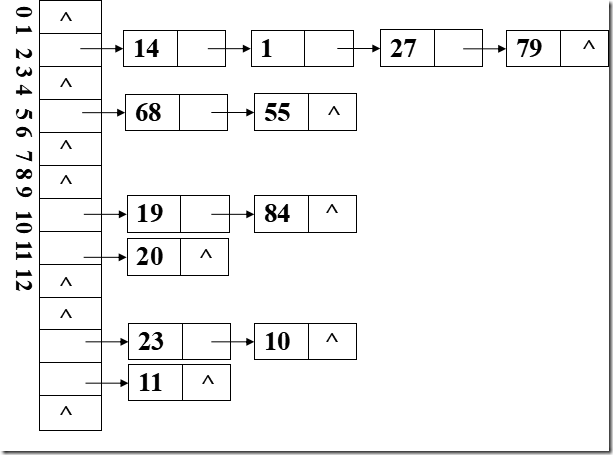

链地址法的优点：

非同义词不会冲突，无“聚集”现象
链表上结点空间动态申请，更适合于表长不确定的情况