改进初学者的PID-测量的比例介绍

　　最近看到了Brett Beauregard发表的有关PID的系列文章，感觉对于理解PID算法很有帮助，于是将系列文章翻译过来！在自我提高的过程中，也希望对同道中人有所帮助。作者Brett Beauregard的原文网址：http：//brettbeauregard.com/blog/2017/06/introducing-proportional-on-measurement/

　　已经有相当长的一段时间了，但我终于更新了Arduino PID库。我添加的是一个几乎未知的功能，但我认为这将是对爱好者社区的利好。它被称为 "测量的比例" (简称 PonM)。

1、为什么你应该关心

　　有一些进程被称为“集成进程”。在这些过程中，PID的输出控制输入的变化率。在工业中，这些只占所有过程的一小部分，但在业余爱好领域，这些家伙无处不在：真空低温烹饪、线性幻灯片和3D打印机挤出机温度控制都是这类过程的例子。

　　这些过程令人沮丧的是，使用传统的 PI 或 PID 控制，它们会超过设定值。不是有时，而是总是：

　　如果你不知道这件事，这可能会让你抓狂。您可以永远调整调优参数，超调仍然存在；基础数学就是这样。测量的比例改变了基础数学。因此，在不发生超调的情况下，可以找到一组调优参数：

　　超调仍然可以肯定，但这并非不可避免。有了 PonM 和正确的整定参数，那个低温烹饪或线性滑块就可以直接延伸到设定值，而不是超过设定值。

2、那么什么是测量的比例呢？

　　与基于测量的微分类似，PonM 改变了比例项所关注的内容。比例项采用PID 输入的当前值代替偏差进行计算。

　　基于偏差的比例：

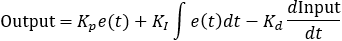
　　基于测量的比例：

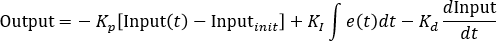
　　与基于测量的微分不同，它对性能的影响是巨大的。对于 DonM，微分项仍然有相同的作用：抵制急剧的变化，从而抑制由P和I比例测量驱动的振荡，另一方面，从根本上改变比例项的作用。它不是像I一样的驱动力，而是像 D 一样成为阻力的力量。这意味着，对于PonM，一个更大的 Kp 将使您的控制器更加保守。

3、很好。但这如何消除超调呢？

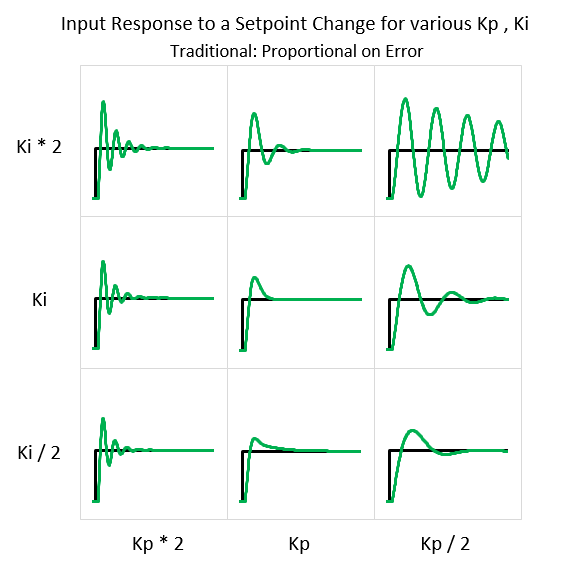
　　要理解这个问题并修复它，看看不同的项以及它们对整个PID输出的贡献是很有帮助的。下面是对使用传统 PID 的集成进程 (真空低温烹饪) 的设定值更改的响应：

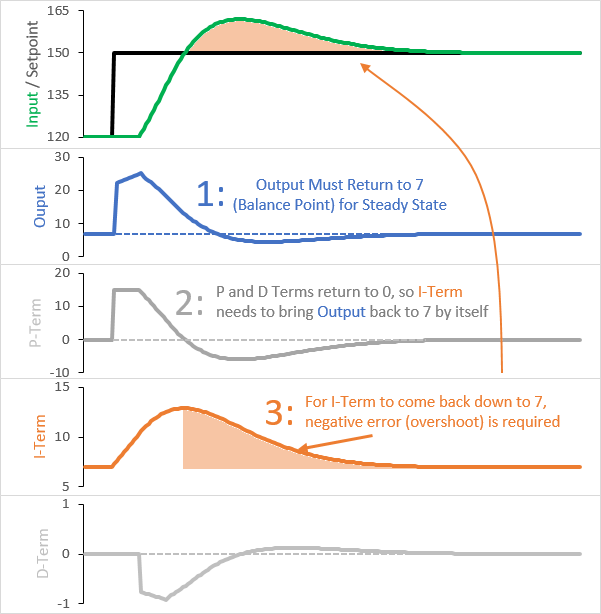
　　需要注意的两大事项是：

1. 当我们处于设定值时，积分项是总体输出的唯一贡献者。
2. 即使起点和终点的设定值不同，输出也会返回到相同的值。此值通常称为“平衡点“：导致0输入斜率的输出。对于真空低温烹饪来说，这相当于足够的热量来补偿周围的热损失。

　　在这里，我们可以看到为什么会发生超调，而且总是会发生。当设定值第一次更改时，偏差将导致积分项的增长。为了使进程在新的设定值保持稳定，输出将需要返回到平衡点。要做到这一点，唯一的办法就是积分项收缩。发生这种情况的唯一方法是负误差，只有在超过设定值时才会发生。

4、PonM改变了游戏规则

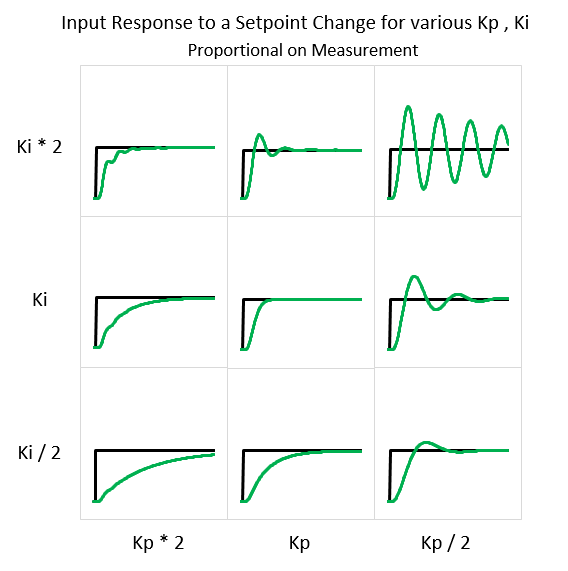
　　下面是使用基于测量的比例 (和相同的调谐参数) 控制的相同的真空低温烹饪：

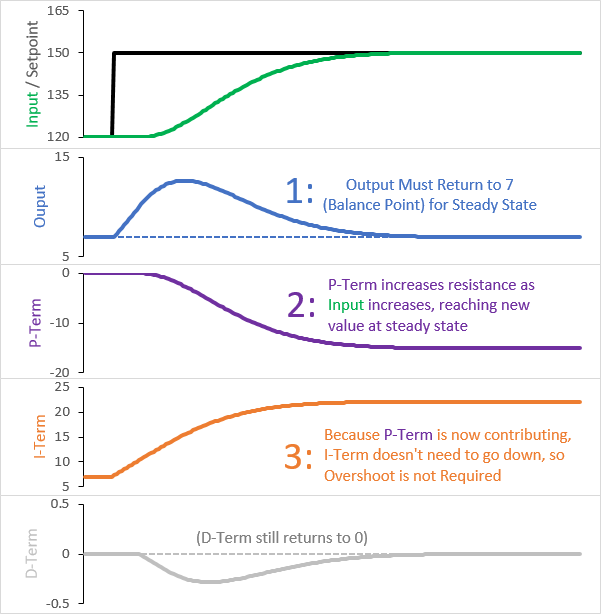
　　在这里，您应该注意到：

1. P项现在提供了一个阻力。输入越高，它就负的越多。
2. P项在新的设定值变为零之前，它会一直有值。

　　关键是P项不会返回到0。这意味着I项不必单独返回到平衡点。P和I一起可以将输出返回到平衡点，而无需收缩I项。因为它不需要收缩，所以不存在超调。

5、如何在新的 PID 库中使用它

　　如果您已准备好尝试 "测量的比例"，并且安装了最新版本的PID库，则设置它是相当容易的。使用 PonM 的主要方法是在重载构造函数中指定它：

　　如果要在运行时在 PonM 和 PonE 之间切换，则 "设置" 函数也会重载：

　　您只需要在需要切换时调用重载方法。否则，您可以使用常规的设置调整功能，它将记住您的选择。

欢迎关注：