PID控制器开发笔记之六：不完全微分PID控制器的实现

　　从PID控制的基本原理我们知道，微分信号的引入可改善系统的动态特性，但也存在一个问题，那就是容易引进高频干扰，在偏差扰动突变时尤其显出微分项的不足。为了解决这个问题人们引入低通滤波方式来解决这一问题。

1、不完全微分的基本思想

　　微分项有引入高频干扰的风险，但若在控制算法中加入低通滤波器，则可使系统性能得到改善。方法之一就是在PID算法中加入一个一阶低通滤波器。这就是所谓的不完全微分，其结构图如下：

或者是另一种形式：

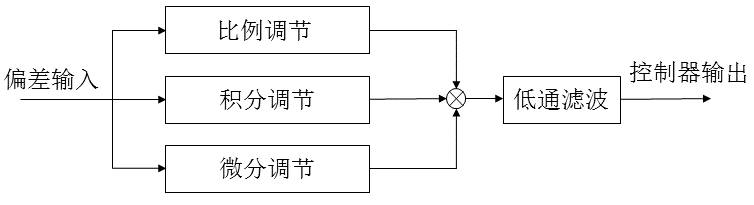
在这里我们考虑第一种结构形式。在这种情况下，微分与一阶惯性环节结合，其微分部分的计算公式可表示如下：

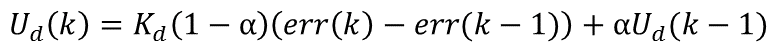
其中α的取值在0和1之间，有滤波常数和采样周期确定。据此我们将其增量化，则可以得到为不完全微分的增量计算公式：

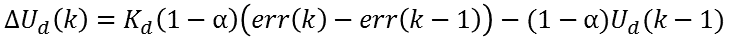
或者表示为：

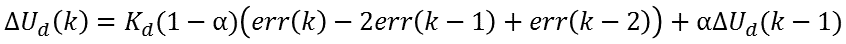
这两种表示方式是等价的，第二种表示法与我们的完全微分PID算法增量型式表示更接近，好理解。而且与位置型的表示法也更为一致，所以我们选择第二种表示法。

2、算法实现

经过前面的分析及公式推导，我们想要实现不完全微分其实已经相当容易了。为了便于理解，我们保持比例和积分为基本的格式，只对微分部分采用不完全微分算法。

（1）位置型PID算法实现

位置型PID实现过程与前面的一样，所不同的是需要增加前一个Ud值。首先定义PID对象的结构体：

 /*定义结构体和公用体*/
 
 typedef struct
 
 {
 
   float setpoint;       //设定值
 
   float proportiongain;     //比例系数
 
   float integralgain;      //积分系数
 
   float derivativegain;    //微分系数
 
   float lasterror;     //前一拍偏差
 
   float lastdev;      //前一拍时的微分项值
 
   float alpha;       //不完全微分系数
 
   float result; //输出值
 
   float integral;//积分值
 
 }PID;

　　接下来实现PID控制器：

 void PIDRegulation(PID *vPID, float processValue)
 
 {
 
   float thisError;
 
   float thisDev;
 
   thisError=vPID->setpoint-processValue;
 
   vPID->integral+=thisError;
 
   thisDev= vPID->derivativegain*(- vPID-> alpha)*(thisError-vPID->lasterror)+ vPID-> alpha* vPID-> lastdev;
 
   vPID->result=vPID->proportiongain*thisError+vPID->integralgain*vPID->integral+ thisDev;
 
   vPID->lasterror=thisError;
 
   vPID->lastdev = thisDev;
 
 }

　　这就实现了一个最简单不完全微分的位置型PID控制器，当然没有考虑任何干扰条件，仅仅只是对数学公式的计算机语言化。

（2）增量型PID算法实现

　　增量型不完全微分PID控制器的实现就是以前面的增量型公式为基础。首先定义PID对象的结构体：

 /*定义结构体和公用体*/
 
 typedef struct
 
 {
 
   float setpoint;       //设定值
 
   float proportiongain;     //比例系数
 
   float integralgain;      //积分系数
 
   float derivativegain;    //微分系数
 
   float lasterror;     //前一拍偏差
 
   float preerror;     //前两拍偏差
 
   float lastdeltadev;      //前一拍时的微分项增量
 
   float alpha;       //不完全微分系数
 
   float deadband;     //死区
 
   float result; //输出值
 
 }PID;

　　接下来实现PID控制器：

 void PIDRegulation(PID *vPID, float processValue)
 
 {
 
   float thisError;
 
   float increment;
 
   float deltaDev;
 
   float pError,dError,iError;
 
   thisError=vPID->setpoint-processValue; //得到偏差值
 
   pError=thisError-vPID->lasterror;
 
   iError=thisError;
 
   dError=thisError-*(vPID->lasterror)+vPID->preerror;
 
   deltaDev= vPID->derivativegain*(- vPID-> alpha)*dError+ vPID-> alpha* vPID-> lastdeltadev;
 
   increment=vPID->proportiongain*pError+vPID->integralgain*iError+ deltaDev;   //增量计算
 
   vPID->preerror=vPID->lasterror;  //存放偏差用于下次运算
 
   vPID->lasterror=thisError;
 
   vPID-> lastdeltadev = deltaDev;
 
   vPID->result+=increment;
 
 }

　　这就实现了一个最简单的增量型不完全微分PID控制器，也没有考虑任何的干扰条件，仅仅只是对数学公式的计算机语言化。

3、总结

　　不完全微分方式在微分环节采用了低通滤波有效地提高了微分项的特性。其中α的取值是一个0~1之间的数。两个极限值，在0时其实就是没有滤波的普通微分环节；而取1时，则没有微分作用。所以α的取值对不完全微分的效果是至关重要的，一般要根据被控对象的特性来确定。

欢迎关注：