洛谷P2181 对角线(组合数)

题目描述

对于一个N个定点的凸多边形，他的任何三条对角线都不会交于一点。请求楚图形中对角线交点的个数。

例如，6边形：

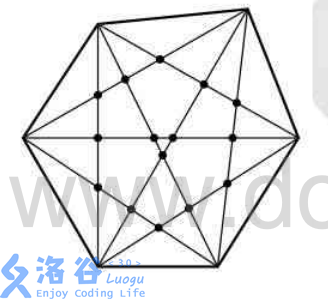
输入输出格式

输入格式：

第一行一个n，代表边数。

输出格式：

第一行输出交点数量

输入输出样例

输入样例#1： 复制

3

输出样例#1： 复制

0

输入样例#2： 复制

6

输出样例#2： 复制

15

说明

50%的测试数据 3≤N≤100;

100%的测试数据 3≤N≤100000.

一道代码难度与思维难度成绝对反比的题目

首先由于不会有三条对角线交于一点，所以过某一个交点有且只能有２条对角线

而这两条对角线实质上是确定了４个顶点（也可以看做是一个四边形的两条对角线交于一点，求四边形的数量）。

因此我们只需要确定４个顶点就得到了这个唯一确定的交点。

因此我们只需要求这样４个顶点的搭配有多少个了

也就是从ｎ个顶点中取４个出来。

根据组合数的公式，（如果你不知道组合数的公式可以这么推：第一次取可以ｎ个点都是可以取的，第二次取的时候第一个取的点就不能取了，所以只能取(n-1)种，以此类推）

由于改变四个点的顺序不会改变对角线，因此是求的组合而不是排列，也就要除以４！，也就是２４

于是我们就得到了公式： n (n-1) (n-2) * (n-3) / 24

输出用unsigned long long

#include<cstdio>
#include<iostream>
using namespace std;
main() {
    unsigned long long N;
    cin>>N;
    cout<<N * (N - ) /   * (N - ) /  * (N - ) / ;
    return ;
}