解题：NOI 2012 骑行川藏

题面

入手点是每段路程中能量$e$与时间$t$的关系，$t-e$这个函数的导数对于各个路段一样，否则我们可以从导数大的一段路抽出一部分能量分给导数小的，这样会更优

毕姥爷在考场上的做法：猜一猜，然后拿python打打表，发现确实是这样的

那么可以把$e/t$化成关于每段速度$v$的一个式子

$e/t$

$=(ks(v-v')^2)/(s/v)$

针对$v$求导

$=k(v-v')/(1/v^2)$

$=kv^2(v-v')$

然后二分这个导数$d$，尝试反解出$v$

$kv^2(v-v')=d$

$v^2(v-v')=d/k$

$v^3-v^2v'-d/k=0$

不幸的是这个东西一点也不好解，所幸$v$大于零，所以这个函数大概长这样↓

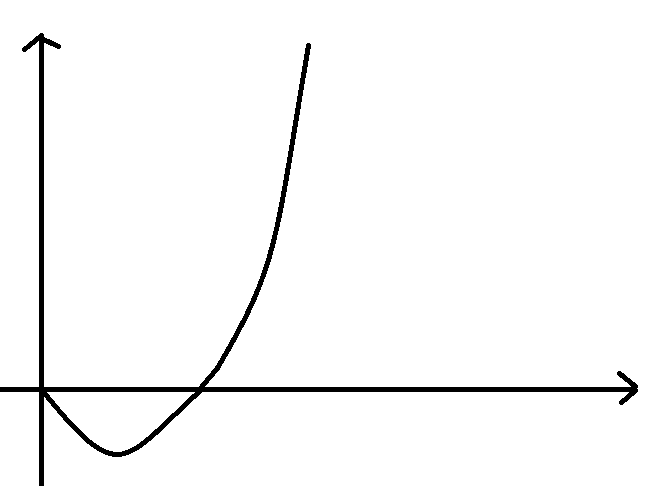
那么这个零点是可以二分出来的，所以再二分一次就好了

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int N=;
 int n; double e,ans,s[N],k[N],v[N];
 double V(double der,int idx)
 {
     double l=,r=1e9;
     for(int i=;i<=;i++)
     {
         double mid=(l+r)/;
         if(mid*mid*mid-mid*mid*v[idx]>=der/k[idx]) r=mid;
         else l=mid;
     }
     return r;
 }
 double Energy(double x)
 {
     double ret=;
     for(int i=;i<=n;i++)
         ret+=s[i]*(V(x,i)-v[i])*(V(x,i)-v[i])*k[i];
     return ret;
 }
 int main()
 {
     scanf("%d%lf",&n,&e);
     for(int i=;i<=n;i++)
         scanf("%lf%lf%lf",&s[i],&k[i],&v[i]);
     double l=,r=1e9;
     for(int i=;i<=;i++)
     {
         double mid=(l+r)/;
         (Energy(mid)>e)?r=mid:l=mid;
     }
     for(int i=;i<=n;i++) ans+=s[i]/V(l,i);
     printf("%f",ans);
 /*    double vv[4]={0,5.12939919,8.03515481,6.17837967};
     for(int i=1;i<=n;i++)
     {
         double t=s[i]/vv[i];
         double g=k[i]*(vv[i]-v[i])*(vv[i]-v[i])*s[i];
         printf("%lf %lf %lf\n",t,g,vv[i]*vv[i]*(vv[i]-v[i])*k[i]);
     }*/
     return ;
 }