USACO 2020 OPEN Silver Problem 3. The Moo Particle

题意：

---

解法：

首先给出在本题中连通和连通块的定义：

连通：

两个粒子a，b连通，当且仅当ax≤bx、ay≤by或者bx≤ax、by≤ay。

如图，A，B两粒子是连通的，而C、D不是。

可以看出，本题中连通的定义类似于无向边。

连通块：

一个有n个粒子的粒子集合S被称为连通块，当且仅当该集合内的粒子可以通过相互作用仅留下任意一个粒子。

左侧的A图中的四粒子属于同一连通块，而右侧的B图中四粒子分别属于两个连通块。

---

50分暴力：

显然，最少留下的粒子（以下简称为点）数等于连通块的总数，故本题可以转化为求最小的连通块划分数。通过该结论可以写出50分暴力（n≤1000）。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + ;
int n, ans, fa[N], dx[N], dy[N];
bool cont (int x, int y) {
    if (dx[x] <= dx[y] && dy[x] <= dy[y])
        return true;
    if (dx[x] >= dx[y] && dy[x] >= dy[y])
        return true;
    return false;
}
int find (int x) {
    if (x != fa[x])
        return fa[x] = find (fa[x]);
    return x;
}
void merges (int x, int y) {
    int xx = find (x), yy = find (y);
    if (xx == yy)
        return ;
    fa[xx] = yy;
    return ;
}
int main () {
    freopen ("moop.in", "r", stdin);
    freopen ("moop.out", "w", stdout);
    scanf ("%d", &n);
    for (int i = ; i <= n; i ++) {
        scanf ("%d %d", &dx[i], &dy[i]);
        fa[i] = i;
    }
    for (int i = ; i <= n; i ++)
        for (int j = i + ; j <= n; j ++)
            if (cont (i, j))
                merges (i, j);
    for (int i = ; i <= n; i ++)
        if (fa[i] == i)
            ans ++;
    printf ("%d\n", ans);
    return ;
}

---

满分解法：

O（n²）暴力连边判断连通块的方法显然是不行的。所以需要找到一种快速划分连通块的方法。

考虑按每个点的x坐标排序并记录排序完成后的y坐标并用数组（a）记录，则可以快速离散化所有点的坐标。（当两点x相同时两点必定连通，故不需要特别讨论x坐标相同的情况）

考虑一个在x轴上连续的点集，满足该点集最左侧的点的y坐标比最右侧的点的y坐标小。（如图）

L、R分别为该点集中最左侧、最右侧的点。

显然，L与R连通。

将点集中剩下的点分为三类：

A类：在R点左上方（如A点）

B类：在R点左下方并且在L点右上方（如B点）

C类：在L点右下方（如C点）

对每类点的连通情况进行讨论：

A类：

因为A点在R点左上方，故A点y坐标比L大、x坐标比L大。所以该点与L点连通。

B类：

因为B点在L点右上方和R点左下方，故与L、R点都连通。

C类：

因为C点在L点右下方，故C点y坐标比R小，x坐标比R小，所以该店与R点连通。

综上所述，A、B、C类点都与L、R中的一点连通，而L又与R点连通。

可得到结论：任意一个满足最左侧的点的y坐标比最右侧的点的y坐标小的在x轴上连续的点集都满足连通块的定义。

由此可以得到一种O（n）的贪心的连通块划分方法：从左往右扫描所有点，若当前点的y值小于上一个点所属的连通块的L点的y值，则从该点开始新建一个连通块，并记录该点的y坐标。

但此贪心方法有明显错误，如图：

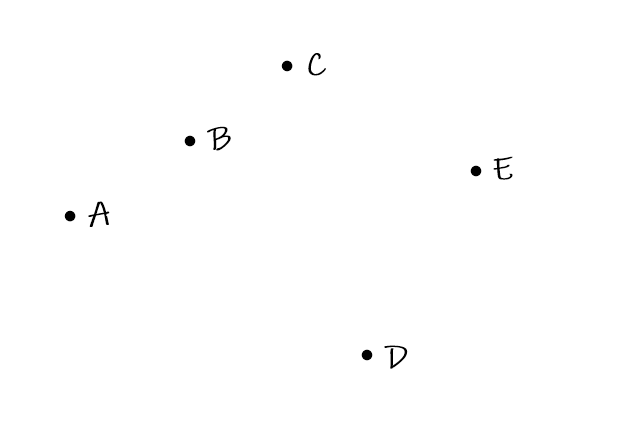
按照这种贪心方法，该点集会被划分为（A、B、C）和（D、E）两个连通块。实际上（A、B、C、D、E）即为一个连通块。

此时可以发现，若记录划分到当前点前每个连通块的L点的y坐标，并在每个点用二分算法判断该点y坐标最大大于哪个L点（设为l点）y坐标并将l点之后的所有点与l点合并为一个连通块，就可以在logn时间内更加准确地判断出到目前点为止最小的连通块划分数。

但这种判断方法仍然有问题，如图：

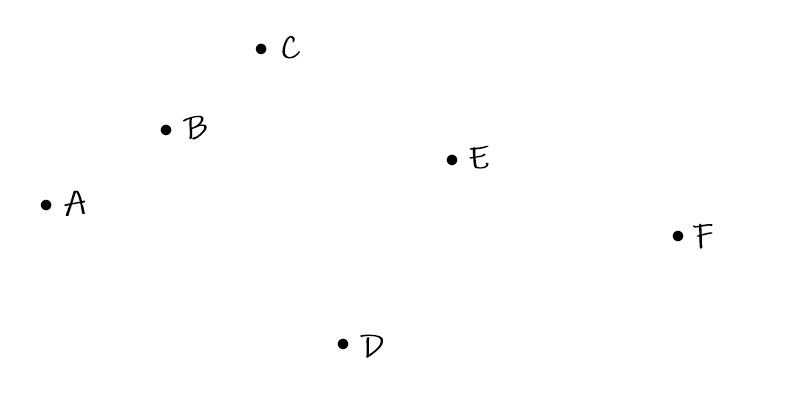
点（A、B、C、D、E、F）为一个连通块，但按照当前贪心方法会划分出（A、B、C、D、E）和（F）两连通块。故我们需要进一步优化贪心方法。

在原贪心方法中，我们记录的是到目前点为止，划分出的所有连通块的L节点的y值，但并入一个连通块并不一定需要大于该连通块的L点，仅需要在该联通块最右侧的点的右侧并大于该连通块的最小点即可。

故在合并连通块的时候，可以把原连通块的L节点的y值更新为现连通块L节点的y值。

这样即可求出最小连通块划分数。

---

代码如下：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + ;
int n, a[N], cnt, mn[N];
pair <int, int> p[N];
int main () {
    freopen ("moop.in", "r", stdin);
    freopen ("moop.out", "w", stdout);
    scanf ("%d", &n);
    for (int i = ; i <= n; i ++)
        scanf ("%d %d", &p[i].first, &p[i].second);
    sort (p + , p + n + );
    for (int i = ; i <= n; i ++)
        a[i] = p[i].second;
    for (int i = ; i <= n; i ++) {
        if (i ==  || -mn[cnt] > a[i]) {
            cnt ++;
            mn[cnt] = -a[i];
            continue ;
        }
        if (cnt == )
            continue;
        if (-mn[cnt - ] <= a[i]) {
            int mnn = mn[cnt];
            int ls = lower_bound (mn + , mn + cnt + , -a[i]) - mn;
            cnt = ls;
            mn[cnt] = mnn;
        }
    }
    printf ("%d\n", cnt);
    return ;
}