L1正则化与L2正则化的理解

1. 为什么要使用正则化

  我们先回顾一下房价预测的例子。以下是使用多项式回归来拟合房价预测的数据：

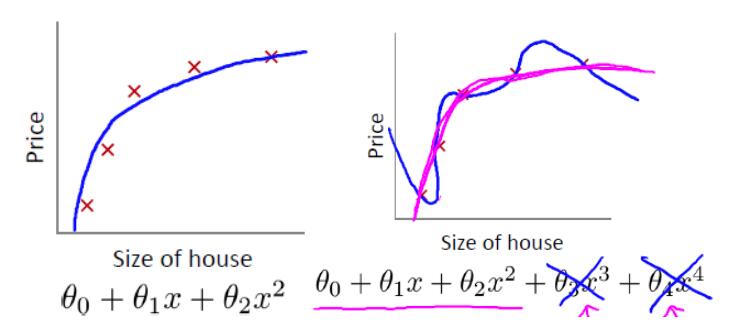
  可以看出，左图拟合较为合适，而右图过拟合。如果想要解决右图中的过拟合问题，需要能够使得 $ x^3，x^4 $ 的参数 $ \theta_3，\theta_4 $ 尽量满足 $ \theta_3 \approx 0 ，\theta_4 \approx 0 $ 。
  而如何使得 $ \theta_3,\theta_4 $ 尽可能接近 $ 0 $ 呢？那就是对参数施一惩罚项。我们先来看一下线性回归的代价函数： \[ J(\theta) = \frac{1}{2m} \sum_{i=1}^{n} (h_\theta(x^{(i)})-y^{(i)})^2 \]
  如果对参数施加惩罚项，式子变为： \[ J(\theta) = \frac{1}{2m} \sum_{i=1}^{n} (h_\theta(x^{(i)})-y^{(i)})^2 + \lambda \sum_{j=0}^{k}\theta_j^2 \]
  梯度下降的式子变为： \[ \theta_j := \theta_j - \frac{\Delta J(\theta)}{\Delta \theta_j} \]
  我们对梯度下降的式子进行推导一下：

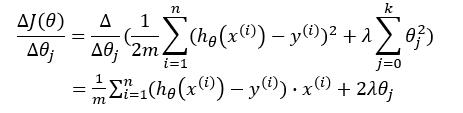
  故： \[ \theta_j := \theta_j - [ \frac{1}{m} \sum_{i=1}^{n}(h_\theta(x^{(i)})-y^{(i)})^2 + 2 \lambda \theta_j ] \]
  由上可以看出，当正则项系数 $ \lambda $ 很大时，对参数的惩罚也将很大，导致在梯度更新后对应的 $ \theta_j $ 值很小。由此可以使得对某些参数最终接近于 $ 0 $ 。而正则项系数 $ \lambda $ 即为模型复杂度的惩罚项，当其很大时，模型复杂度将变小，也就是模型将更为简单，不会使得对数据过于拟合。
  从结构风险最小化角度来说，就是在经验风险最小化的基础上（即训练误差最小化），尽可能采用简单的模型，以此提高泛化预测精度。
  这一小节我们直观地了解了为何要使用正则化项，接下来我们从理论上来分析一下。

---

2. L1正则化与L2正则化

  这一小节参考自博客1。
  依旧以线性回归为例（只含有两个参数的情况，此处的参数 $ w $ 与上一节中的 $ \theta $ 一致，只是本节中为了与图片上的参数相对应，而将参数使用 $ w $ 进行表示）。加上L1正则化后的优化目标（lasso回归）： \[ min \frac{1}{2m} \sum_{i=1}^{n} (h_w(x^{(i)})-y^{(i)})^2 + \lambda \sum_{j=1}^{2} |w_j| \]
  加上L2正则化后的优化目标（岭回归）： \[ min \frac{1}{2m} \sum_{i=1}^{n} (h_w(x^{(i)})-y^{(i)})^2 + \lambda \sum_{j=1}^{2}w_j^2 \]
  使用等高线图来表示原目标函数的图像为：

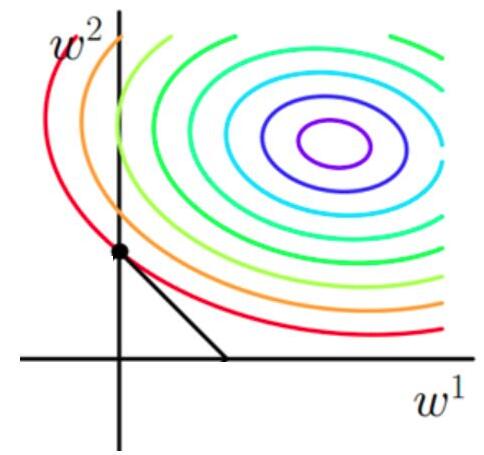
  也就是说，当参数 $ w_1 与 w_2 $ 取值为图像中最里面那个紫色圆圈上的值时，可以使得原目标函数最小。
  当加上L1正则项之后，目标函数图像为：

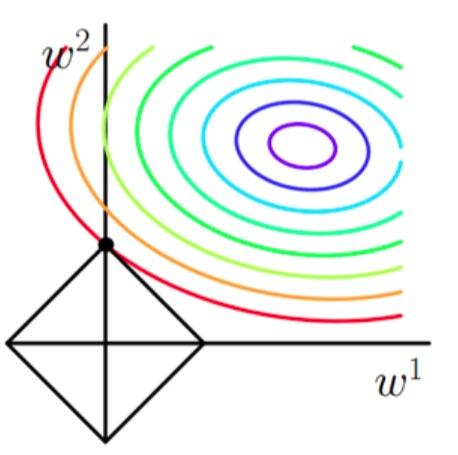
  当加上L2正则项之后，目标函数图像为：

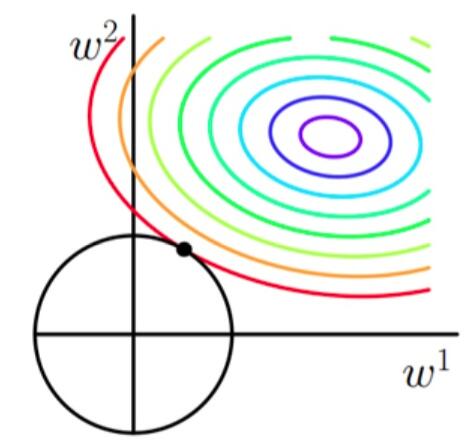
  第一个图中菱形即为 $ \sum_{j=1}^{2}|w_j| = F $ ，而第二个图中圆形即为 $ \sum_{j=1}^{2}w_j^2 = F $ 。代表这个菱形（圆形）上的点算出来的 $ \sum_{j=1}^{2}|w_j| 或 \sum_{j=1}^{2}w_j^2 $ 都等于某个值 $ F $ 。此时若要使得目标函数最小，就需要满足两个条件：（1）参数值在等高线上的圆圈越来越接近中心的紫色圆圈，（2）菱形越小越好（ $ F $ 越小越好）。
  那么如何取得一个恰好的值，能够满足以上两个条件呢？我们先来看下下面这个图（以L1正则化为例）：

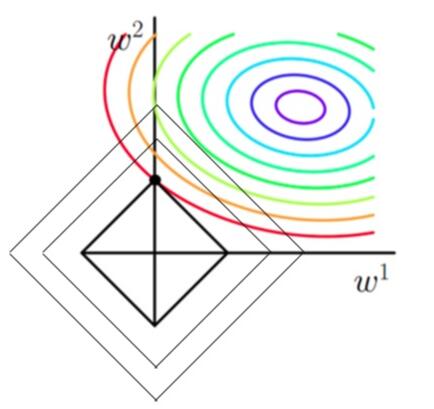
  以同一条原曲线目标等高线来说，现在以最外圈的红色等高线为例，我们看到，对于红色曲线上的每个点都可以做一个菱形，根据上图可知，当这个菱形与某条等高线相切（仅有一个交点）的时候，这个菱形最小，上图相割对比较大的两个菱形对应的L1正则化项更大。也就是说，相切时在使得 $ \frac{1}{2m} \sum_{i=1}^{n} (h_w(x^{(i)})-y^{(i)})^2 $ 相同的情况下， $ \lambda \sum_{j=1}^{2}|w_j| $ 最小，因此，该点能够使得 $ \frac{1}{2m} \sum_{i=1}^{n} (h_w(x^{(i)})-y^{(i)})^2 + \lambda \sum_{j=1}^{2} |w_j| $ 最小。
  由以上结论，我们可以看出，要使得加入L1正则化的解，一定是某个菱形和某条原函数等高线的切点。而通过观察我们可以看出，几乎对于很多原函数等高曲线，和某个菱形相交的时候及其容易相交在坐标轴（比如上图），也就是说最终的结果，解的某些维度及其容易是 $ 0 $ ，比如上图最终解是 $ w = （0，x）$ ，这也就是我们所说的L1更容易得到稀疏解（解向量中0比较多）的原因。
  接下来我们使用公式进行推导一下看。假设现在是在一维的情况下，目标函数看做是 $ J(w) = f(w) + \lambda |w| $ ,其中 $ f(w) $ 为原目标函数， $ J(w) $ 为加了L1正则项之后的目标函数。 $ \lambda |w| $ 是正则化项。那么要使得 $ 0 $ 点成为最值可能的点，即使在 $ 0 $ 点不可导，但是只需要让函数在 $ 0 $ 点左右的导数异号。即 $ J'_左(w) \times J'_右(w) = (f'(0) + \lambda) \times (f'(0) - \lambda) < 0 $ ，也就是 $ \lambda > |f'(0)| $ 时， $ 0 $ 点都是可能的最值点。
  当加入L2正则化的时候，分析和L1正则化是类似的，也就是说我们仅仅是从菱形变成了圆形而已，同样还是求原曲线和圆形的切点作为最终解。当然与L1范数比，我们这样求的L2范数的从图上来看，不容易交在坐标轴上，但是仍然比较靠近坐标轴。因此这也就是我们老说的，L2范数能让解比较小（靠近0），但是比较平滑（不等于0）。
  综上所述，我们可以看见，加入正则化项，在最小化经验误差的情况下，可以让我们选择解更简单（趋向于0）的解。因此，加正则化项就是结构风险最小化的一种实现。

---

引用及参考：
[1] https://zhuanlan.zhihu.com/p/35356992?utm_medium=social&utm_source=wechat_session
[2] https://blog.csdn.net/pakko/article/details/37878837
[3] https://www.zhihu.com/question/37096933/answer/70426653

写在最后：本文参考以上资料进行整合与总结，属于原创，文章中可能出现理解不当的地方，若有所见解或异议可在下方评论，谢谢！
若需转载请注明：https://www.cnblogs.com/lliuye/p/9354972.html