P4208 [JSOI2008]最小生成树计数

现在给出了一个简单无向加权图。你不满足于求出这个图的最小生成树，而希望知道这个图中有多少个不同的最小生成树。（如果两颗最小生成树中至少有一条边不同，则这两个最小生成树就是不同的）输出方案数对31011的模

摘自大佬博客：

https://blog.sengxian.com/solutions/bzoj-1016

http://www.cnblogs.com/Y-E-T-I/p/8462255.html#undefined

https://kelin.blog.luogu.org/solution-p4208

https://cnyali-lk.blog.luogu.org/solution-p4208

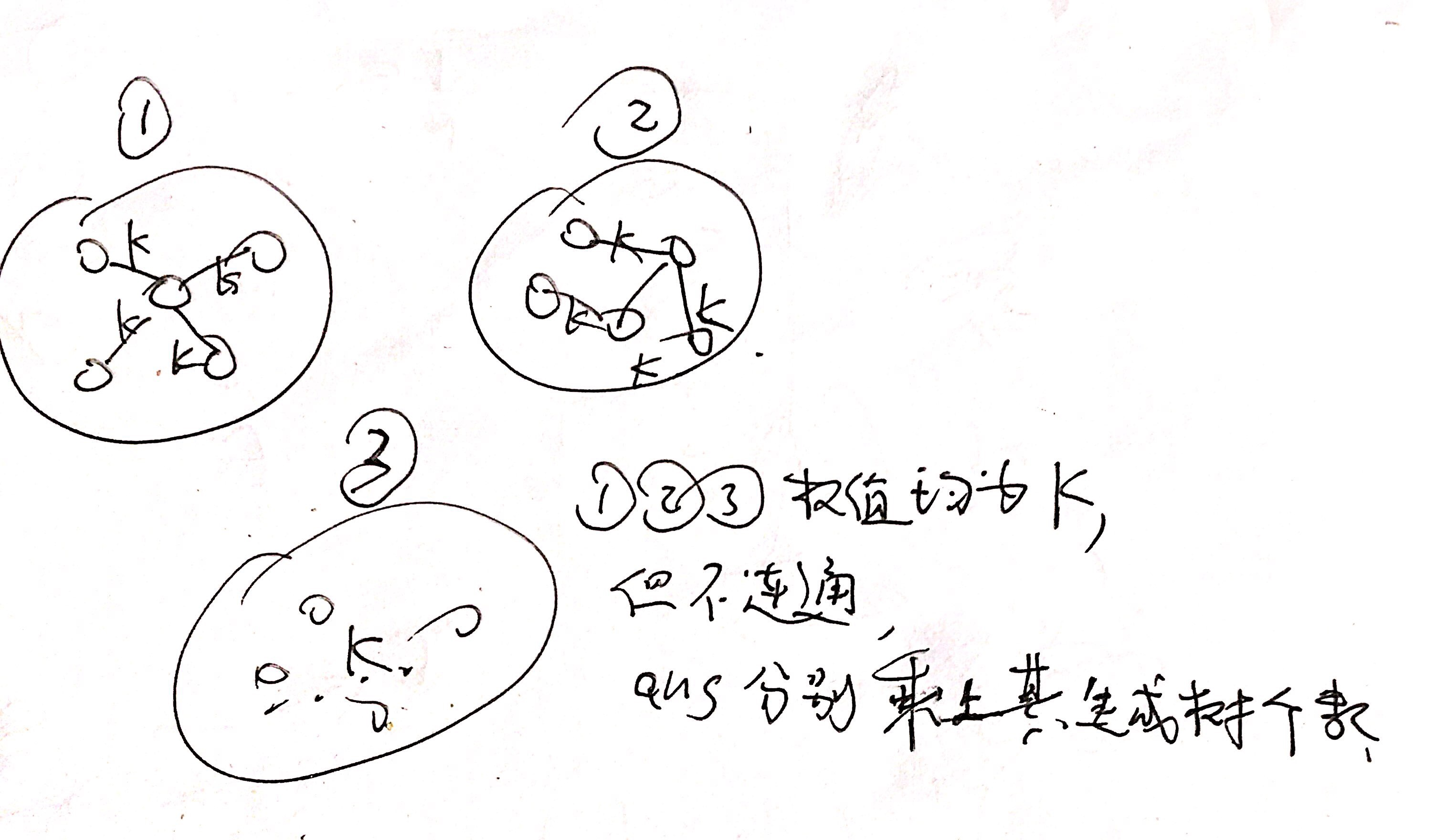
#include <bits/stdc++.h>
#define fp(i, a, b) for (register int i = a, I = b + 1; i < I; ++i)
#define fd(i, a, b) for (register int i = a, I = b - 1; i > I; --i)
#define go(u) for (register int i = fi[u], v = e[i].to; i; v = e[i = e[i].nx].to)
#define file(s) freopen(s ".in", "r", stdin), freopen(s ".out", "w", stdout)
template <class T>
inline bool cmax(T &a, const T &b) { return a < b ? a = b,  : ; }
template <class T>
inline bool cmin(T &a, const T &b) { return a > b ? a = b,  : ; }
using namespace std;
const int N = , M = , P = ;
typedef int arr[N];
struct eg
{
    int u, v, w;
} e[M];
int n, m, ans = ;
arr fa, bl, vis, g[N], G[N];
vector<int> s[N];
int gf(int u, int *fa) { return fa[u] == u ? u : fa[u] = gf(fa[u], fa); }//find并查集
inline int pls(int a, int b) { return a += b, a >= P ? a - P : a; }//模数不为质数的操作
inline int sub(int a, int b) { return a -= b, a <  ? a + P : a; }
inline int det(int n)//返回缩点的生成树个数
{
    int a, b, t, f = , tp = ;
    fp(i, , n) fp(j, , n) G[i][j] = pls(P, G[i][j]);
    fp(i, , n)
    {
        fp(j, i + , n)
        {
            a = G[i][i], b = G[j][i];
            while (b)
            {
                t = a / b;
                a %= b;
                swap(a, b);
                fp(k, i, n) G[i][k] = sub(G[i][k], t * G[j][k] % P);
                fp(k, i, n) swap(G[i][k], G[j][k]);
                f = -f;
            }
        }
        if (!G[i][i])
            return ;
        tp = tp * G[i][i] % P;
    }
    return pls(P, f * tp);
}
inline void calc()//合并联通块形成缩点
{
    fp(i, , n) if (vis[i])
    {
        s[gf(i, fa)].push_back(i);
        vis[i] = ;
    }
    fp(i, , n) if (s[i].size() > )
    {
        int t = s[i].size(), *a = s[i].data();
        memset(G, , sizeof G);
        fp(j, , t) fp(k, j + , t)
        {
            int u = a[j - ], v = a[k - ];
            if (g[u][v])
            {
                G[j][k] = G[k][j] = -g[u][v];
                G[j][j] += g[u][v], G[k][k] += g[u][v];
            }
        }
        ans = ans * det(t - ) % P;
        fp(j, , t) bl[a[j - ]] = i;//属于同一联通块
    }
    fp(i, , n) s[i].clear(), fa[i] = bl[i] = gf(i, bl);
}
inline bool cmp(const eg &a, const eg &b) { return a.w < b.w; }
int main()
{
#ifndef ONLINE_JUDGE
    file("s");
#endif
    scanf("%d%d", &n, &m);
    fp(i, , n) fa[i] = bl[i] = i;
    fp(i, , m) scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
    sort(e + , e + m + , cmp);
    e[] = e[];
    fp(i, , m)
    {
        //发现不相同的边界点就计算处理
        if (e[i].w ^ e[i - ].w)
            calc();
            //同一权值合并
        int u = gf(e[i].u, bl), v = gf(e[i].v, bl);
        if (u ^ v)
        {
            vis[u] = vis[v] = ;
            ++g[u][v], ++g[v][u];
            fa[gf(u, fa)] = gf(v, fa);
        }
    }
    calc();
    fp(i, , n) if (bl[i] ^ bl[i - ]) return puts(""), ;
    printf("%d", ans);
    return ;
}