python实现圆检测

目录：

（一）霍夫圆检测原理

（二）代码实现

（一）霍夫圆检测原理

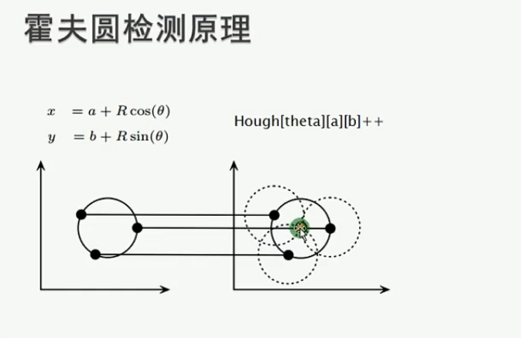
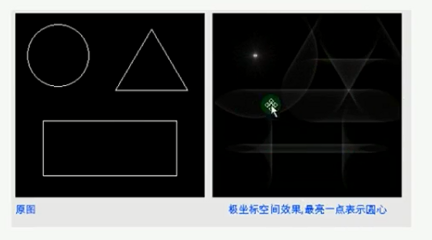
（二）代码实现

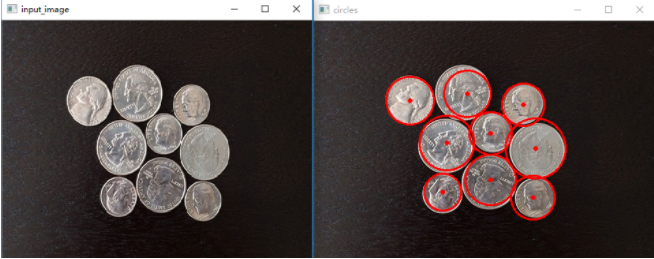
 1 #霍夫圆检测
 2 import cv2 as cv
 3 import numpy as np
 4
 5 def detect_circles_demo(image):
 6     dst = cv.pyrMeanShiftFiltering(image, 10, 100)   #边缘保留滤波EPF
 7     cimage = cv.cvtColor(dst, cv.COLOR_RGB2GRAY)
 8     circles = cv.HoughCircles(cimage, cv.HOUGH_GRADIENT, 1, 20, param1=50, param2=30, minRadius=0, maxRadius=0)
 9     circles = np.uint16(np.around(circles)) #把circles包含的圆心和半径的值变成整数
10     for i in circles[0, : ]:
11         cv.circle(image, (i[0], i[1]), i[2], (0, 0, 255), 2)  #画圆
12         cv.circle(image, (i[0], i[1]), 2, (0, 0, 255), 2)  #画圆心
13     cv.imshow("circles", image)
14
15 src = cv.imread('E:/imageload/coins.jpg')
16 cv.namedWindow('input_image', cv.WINDOW_NORMAL) #设置为WINDOW_NORMAL可以任意缩放
17 cv.imshow('input_image', src)
18 detect_circles_demo(src)
19 cv.waitKey(0)
20 cv.destroyAllWindows()

注意：

1.OpenCV的霍夫圆变换函数原型为：HoughCircles(image, method, dp, minDist[, circles[, param1[, param2[, minRadius[, maxRadius]]]]]) -> circles

image参数表示8位单通道灰度输入图像矩阵。

method参数表示圆检测方法，目前唯一实现的方法是HOUGH_GRADIENT。

dp参数表示累加器与原始图像相比的分辨率的反比参数。例如，如果dp = 1，则累加器具有与输入图像相同的分辨率。如果dp=2，累加器分辨率是元素图像的一半，宽度和高度也缩减为原来的一半。

minDist参数表示检测到的两个圆心之间的最小距离。如果参数太小，除了真实的一个圆圈之外，可能错误地检测到多个相邻的圆圈。如果太大，可能会遗漏一些圆圈。

circles参数表示检测到的圆的输出向量，向量内第一个元素是圆的横坐标，第二个是纵坐标，第三个是半径大小。

param1参数表示Canny边缘检测的高阈值，低阈值会被自动置为高阈值的一半。

param2参数表示圆心检测的累加阈值，参数值越小，可以检测越多的假圆圈，但返回的是与较大累加器值对应的圆圈。

minRadius参数表示检测到的圆的最小半径。

maxRadius参数表示检测到的圆的最大半径。

2.OpenCV画圆的circle函数原型：circle(img, center, radius, color[, thickness[, lineType[, shift]]]) -> img

img参数表示源图像。

center参数表示圆心坐标。

radius参数表示圆的半径。

color参数表示设定圆的颜色。

thickness参数：如果是正数，表示圆轮廓的粗细程度。如果是负数，表示要绘制实心圆。

lineType参数表示圆线条的类型。

shift参数表示圆心坐标和半径值中的小数位数。