Coursera在线学习---第四节.过拟合问题

一、解决过拟合问题方法

1）减少特征数量

--人为筛选

--靠模型筛选

2）正则化(Regularization)

原理：可以降低参数Θ的数量级，使一些Θ值变得非常之小。这样的目的既能保证足够的特征变量存在(虽然Θ值变小了，但是并不为0)，还能减少这些特征变量对模型的影响。换言之，这些特征对于准备预测y值依然能发挥微小的贡献，这样也避免了过拟合问题。(个别Θ值过大，容易过拟合，如果Θ=0，等于缺少个别特征变量，对模型依然不好)

二、具体实例

     通常我们并不知道具体使哪些Θ值变小，所以我们就让Θ1，Θ2，...，Θ100 都变小，不包括Θ0。

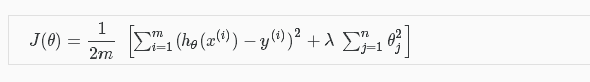
λ为正则化参数

有了正则化参数 λ就能使后面的Θ1-Θj变小了，因为如果后面的Θ值不变小，J(Θ)的值就会太大了，所以在减小J(Θ)值的过程中会逼着减小Θ的值。

λ值过大，会让Θ1-Θj的值变得非常非常小，这样就只有Θ0的值非常大，几乎变成了y=Θ0一条直线了，会造成欠拟合问题。所以，λ的值应该比较合理才行。另外，正则化参数过多也会出现该问题，可以适时减少参与正则化的参数，例如从Θ2-Θj开始参与正则化等等。

备注：如果模型在训练样本上就表现不好，说明模型欠拟合，需要增加更多的特征变量，可以引入多项式回归(Θ0+Θ1*X+Θ2*X^2+Θ3*X^3)，多项式回归方程能让曲线更加弯曲以适应训练样本。这样能更好的拟合训练样本，或者减少正则化参数（例如：从Θ2开始正则化）