正则化项本质上是一种先验信息，整个最优化问题从贝叶斯观点来看是一种贝叶斯最大后验估计，其中正则化项对应后验估计中的先验信息，损失函数对应后验估计中的似然函数，两者的乘积即对应贝叶斯最大后验估计的形式，如果你将这个贝叶斯最大后验估计的形式取对数，即进行极大似然估计，你就会发现问题立马变成了损失函数+正则化项的最优化问题形式。

　　

　　在原始的代价函数后面加上一个L1正则化项，即所有权重w的绝对值的和，乘以λ/n:

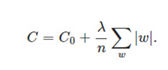
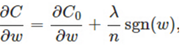
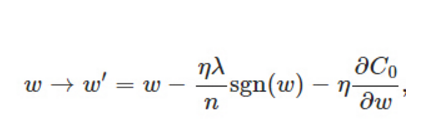
　　比原始的更新规则多出了η * λ * sgn(w)/n这一项。当w为正时，更新后的w变小。当w为负时，更新后的w变大——因此它的效果就是让w往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。当w为0时怎么办？当w等于0时，|W|是不可导的，所以我们只能按照原始的未经正则化的方法去更新w，这就相当于去掉η*λ*sgn(w)/n这一项，所以可以规定sgn(0)=0，这样就把w=0的情况也统一进来了。（在编程的时候，令sgn(0)=0,sgn(w>0)=1,sgn(w<0)=-1）

　　

L1正则化的更多相关文章

  1. L1正则化及其推导

    \(L1\)正则化及其推导 在机器学习的Loss函数中,通常会添加一些正则化(正则化与一些贝叶斯先验本质上是一致的,比如\(L2\)正则化与高斯先验是一致的.\(L1\)正则化与拉普拉斯先验是一致的等 ...

  2. Laplace（拉普拉斯）先验与L1正则化

    Laplace(拉普拉斯)先验与L1正则化 在之前的一篇博客中L1正则化及其推导推导证明了L1正则化是如何使参数稀疏化人,并且提到过L1正则化如果从贝叶斯的观点看来是Laplace先验,事实上如果从贝 ...

  3. 【深度学习】L1正则化和L2正则化

    在机器学习中,我们非常关心模型的预测能力,即模型在新数据上的表现,而不希望过拟合现象的的发生,我们通常使用正则化(regularization)技术来防止过拟合情况.正则化是机器学习中通过显式的控制模 ...

  4. L1正则化比L2正则化更易获得稀疏解的原因

    我们知道L1正则化和L2正则化都可以用于降低过拟合的风险,但是L1正则化还会带来一个额外的好处:它比L2正则化更容易获得稀疏解,也就是说它求得的w权重向量具有更少的非零分量. 为了理解这一点我们看一个 ...

  5. L2与L1正则化理解

    https://www.zhihu.com/question/37096933/answer/70507353 https://blog.csdn.net/red_stone1/article/det ...

  6. L1正则化和L2正则化

    L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择 L2正则化可以防止模型过拟合(overfitting):一定程度上,L1也可以防止过拟合 一.L1正则化 1.L1正则化 需注意, ...

  7. L1正则化与L2正则化的理解

    1. 为什么要使用正则化   我们先回顾一下房价预测的例子.以下是使用多项式回归来拟合房价预测的数据:   可以看出,左图拟合较为合适,而右图过拟合.如果想要解决右图中的过拟合问题,需要能够使得 $ ...

  8. 正则化--L1正则化（稀疏性正则化）

    稀疏矢量通常包含许多维度.创建特征组合会导致包含更多维度.由于使用此类高维度特征矢量,因此模型可能会非常庞大,并且需要大量的 RAM. 在高维度稀疏矢量中,最好尽可能使权重正好降至 0.正好为 0 的 ...

  9. LASSO回归与L1正则化 西瓜书

    LASSO回归与L1正则化 西瓜书 2018年04月23日 19:29:57 BIT_666 阅读数 2968更多 分类专栏: 机器学习 机器学习数学原理 西瓜书   版权声明:本文为博主原创文章,遵 ...

随机推荐

  1. oracle修改字符集方法

    查看源数据库字符集 在sql命令行执行,即可查看 cat exp.dmp |od -x|head -1|awk '{print $2 $3}'|cut -c 3-6 例如我的返回结果为0362,对照以 ...

  2. 关于 TypeReference 的解释

    首先 TypeReference  是描述 一个复杂 泛型的工具类. TypeReference 很多类库都有,用 fastjson 的 举例,大概就这个意思. 例子: Response<Fee ...

  3. php保留两位小数的3种方法

    <?php $num = 8.16789; //第一种:利用round()对浮点数进行四舍五入 echo round($num,2).PHP_EOL; //8.17 //第二种:利用sprint ...

  4. dashboard无法查到endpoint, counter

    问题 使用Open-falcon时,Agent 推送metrics后,无法在Dashboard上显示.将Agent的hostname 修改后,却可以. 解决办法 查看Agent log,推送到tran ...

  5. zabbix moniter

    zabbix moniter http://blog.csdn.net/xiegh2014/article/category/6945291/2

  6. GetClass与RegisterClass的应用一例

    利用GetClass与RegisterClass可以实现根据字符串来实例化具体的子类,这对于某些需要动态配置程序的场合是很有用的.其他的应用如子窗体切换,算法替换等都能得到应用. unit Examp ...

  7. ubuntu-docker入门到放弃（二）docker初探（基本用法及命令）

    一.使用公共镜像 docker有一个开源的镜像管理系统,上面有很多常见的images,如mysql,nginx,tomcat等,可以直接根据自己的需求下载下来用,还有系统images,如redhat, ...

  8. 关于此实现不是 Windows 平台 FIPS 验证的加密算法的一部分。

    注册表进入如下路径中 HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Control\Lsa\FipsAlgorithmPolicy 将 enable设置为0 ...

  9. C# DataAdapter.Update() 无法更新数据表中删除的数据行

    用DataAdapter.Update() 方法更新删除了部分DataRow 的 DataTable .但是数据库中的数据没有随着更新而变化. 原因:DataTable 删除 DataRow 时,使用 ...

  10. webGL之three.js入门4--ThreeJS Editor入门篇

    因为工作需要,要看threejs editor的源码,顺便记录过程. github下载的源码目录是这样的 但是editor和其他文件夹内的内容的关联的,我需要将其独立出来并且编辑editor. 进入e ...