Chapter 7:Statistical-Model-Based Methods

作者：桂。

时间：2017-05-25  10:14:21

主要是《Speech enhancement: theory and practice》的读书笔记，全部内容可以点击这里。

书中代码：http://pan.baidu.com/s/1hsj4Wlu，提取密码：9dmi

---

前言

　　最近学习有一点体会，每一个学科的理论模型都提供了解决问题的思路，一个没有受过教育又迷信权威的头脑，难以从抽象的角度去认识、理解问题，自然科学传递了这样一套思维。例如之前的谱减法，就是具体问题具体分析;维纳滤波，表达了复盘、以及反馈总结的重要性;这一章的统计模型，表达了对于不善于长期记忆的人类，借助历史信息可以获得更多的益处。总结一下，这些模型都表明：认识问题要经过感性-理性-感性的往复过程，很难有一劳永逸的方法，这也提醒思考的时候要小心、并保持客观（因为总有新问题），避免陷入刚愎自用的误区，同时也不必灰心丧气，从Ada-boost的角度来看，任何弱分类器都可以组合成强分类器，自己/他人的经历、经验增加（无论真假，只要努力推理出真与假的倾向），一个基本事实是：合理利用这些信息，总会让人更接近事实真相。具体来说，对于语音降噪，都有：意识到问题——拆解并解决问题 的步骤，这也说明了一个现象：学习、记忆、认知，这些 靠眼耳鼻舌身意 直观接受的过程，如果二次加工，那么效果将会进一步提升。

　　这一章主要是利用统计模型，细节处打算跳过，主要是三种模型：最大似然估计ML、最小均方误差估计MMSE、最大后验估计MAP。

一、最大似然估计：MAXIMUM-LIKELIHOOD ESTIMATORS

　　A-最大似然估计

加性噪声模型

写成幅频形式

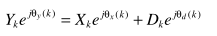
为了求解，给出两点假设：1）虽然未知，但是确定信号，而不是随机信号;2）噪声是复高斯分布，且实部、虚部的方差相同;

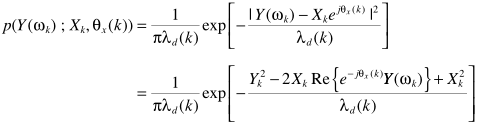
这个求解比较复杂，且仍然可以用带噪声的相位近似，这样一来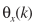就是无关紧要的了，可以对上面的式子进一步处理：

这里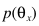是未知的，这里强行用了另一个约束：在没有先验的情况下，均匀分布信息量最大，也就是不确定性最大，这也符合没有先验之一预期，从而

上式简化为

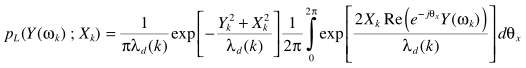
这里积分部分满足Bessel的定义

零阶Bessel可近似：

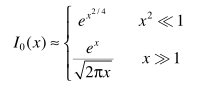
近似的结果

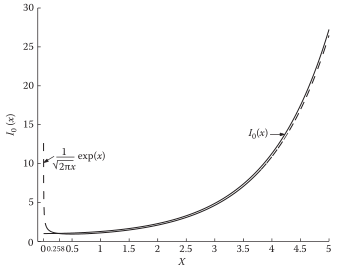
利用Bessel近似表达似然函数

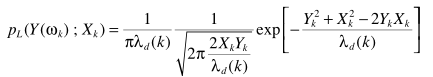
导数为零求解出幅度谱估计

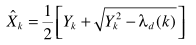
恢复降噪的信号

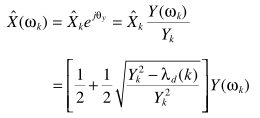
从这一结果也可以看出X = 1/2Y + 1/2HY，总是有部分保留，ML衰减是较小的，也正因为如此，ML估计器基本不单独使用，需要配合其他模型使用：如利用语音不存在概率。

　　B-功率谱减

与ML估计器不同，这里不再假定是确定信号，而是随机信号。

既然是随机信号，就有统计信息。因此给出假设：噪声、语音信号的DFT不相关，且都服从零均值的高斯分布。从而得出Y概率密度

容易估计幅度谱

得到恢复的音频

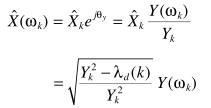
这就是功率谱减，即（γ为后验信噪比）

　　C-维纳滤波

对于维纳滤波器

变换一下形式

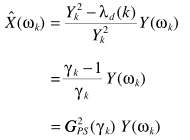
滤波器是功率谱减的级联，因此衰减最大。

总计一下：按衰减程度由大到小，关系依次是：维纳滤波>功率谱减>最大似然估计

二、贝叶斯估计 BAYESIAN ESTIMATORS

 　　A-MMSE幅值估计器

基于短时频谱幅值的方法有个专业术语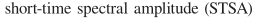：，最优幅度谱估计：

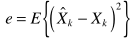
根据联合密度

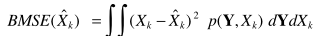
得到最优估计器

看着感觉跟Wiener滤波器一回事，其实是有区别的：1）Wiener中，X = HY，假设有线性关系，这里没有线性这一约束，也就是说这里的估计器可以是非线性的; 2）维纳的MMSE是复频谱最优，而此处的MMSE是幅度谱最优。

同样是为了简化，引入约束1：各个频点的DFT系数相互独立：

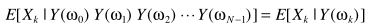
这样一来求解问题简化为：

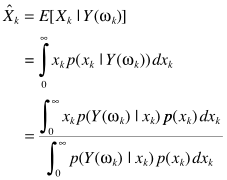
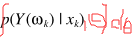由于复信号Y是关于Xk和theta的函数，难以直接求取，只要利用联合分布积分处理即可，也就是

这样一来求解红框里的两个方程就可以得出理论解。这里引入约束2：Y是两个零均值的复高斯随机变量之和。

则

这里用到复高斯概率密度的性质：

如果：且则

且两高斯分布：其模值为瑞利分布，相位为均匀分布，且二者独立，证明可以参考这里。从而

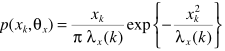
事实上，至此完成了问题的求解，得到X_k的估计。但牛人们非要给一个更简洁的表达式，这里直接给出结果：

具体参数的定义，直接引用原文：

理论模型搭建完成，甚至得出了更简洁的形式，距离应用只差一步——参数的近似估计。文中的基本方法有两个：

1-Maximum-Likelihood Method

利用多帧信号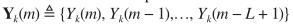：，求解似然方程

容易得出估计（因为是非零，所以max(估值，0)修正一下）

从而有

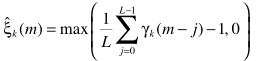
2-Decision-Directed Approach

根据定义

进一步写成

一个常规的思路是分两边看，借助递归思想，因为：

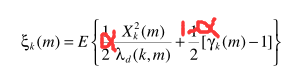
得出递归的更新公式

至此，完成了MMSE从理论到应用的整个过程。

　　B-MMSE复数估计器

上面是幅值估计，相位用的是带噪信号的相位，可不可以直接对复信号利用MMSE进行估计呢？

求解问题转化为：分别利用MMSE求解幅值、相位的最优解，幅值已解决，直接分析相位

可以得出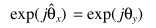，所以带噪信号的相位是干净信号相位在MMSE下的最优解。

　　C-对数MMSE估计器

求解思路与幅值的MMSE完全相同，不同的是利用对数的差异性

首先带来一个问题：为什么要用Log-MMSE？个人理解是logx - logy = logx/y，min|x/y|等价于min(x-y)² s.t. y² = c,c为常数。log相比于直接MMSE，保证干净信号幅值不变（不失真）的前提下，误差最小化，有点类似维纳滤波与LCMV之间的关系。理论上直接求解估值

无法直接求解，利用矩量简化求解

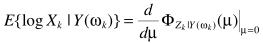
其中

跟MMSE求解一个思路，至此完成求解。但牛人们也希望简化

从而实现简化求解

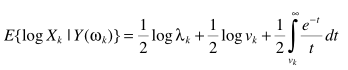
v_k, λ_k跟上面的定义一样，进一步简化

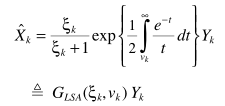
参数估计与MMSE中的思路完全一致，至此完成了求解以及实际应用的实现，其中积分部分也可以利用级数展开来简化

Log-MMSE比MMSE抑制性更好：

　　D-pTH-POWER SPECTRUM-P阶求解

先说结论：p阶是更广义的形式，Linear MMSE是它的特例，Log-MMSE也可以用p阶来实现逼近

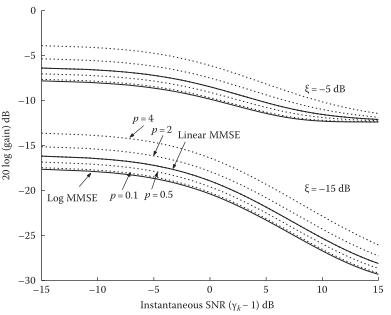
下面理论分析一下，给出准则函数

得出最优估计

都是一样的套路：不能直接求解，转化问题

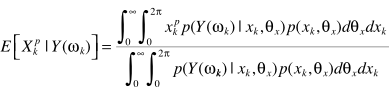
大牛们求解的结果

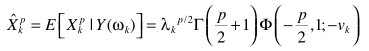
即

具体参数求解同MMSE中的方法。

　　E-非高斯分布MMSE估计器

上面的DFT系数分布，都假设为高斯分布，实际情况是分布可能更接近其他分布（按频点统计）：如拉普拉斯、伽马分布等等，这就需要考虑其他概率模型

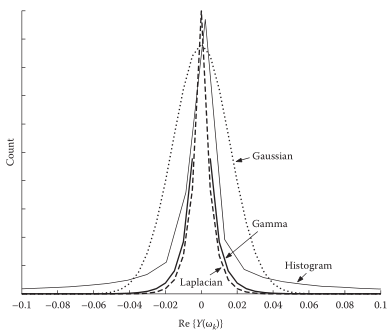
一个合理的约束：DFT系数实部、虚部统计独立。这样互不相干，可以分别得出MMSE估计器，再进行拼接：

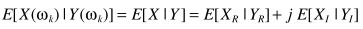
其他思路都是一样的，就是最后解方程一般人解不动...说一下思路：

根据贝叶斯定理

同样只要估计出P（Y|X）和P（Y）就完成求解

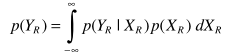
从而得出估计器，完成求解

大牛总是可以简化问题的，虽然这次的简化好像也不漂亮：

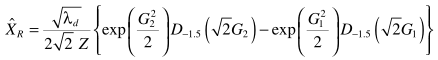
其中

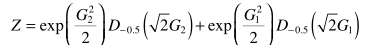
以上是基于Gamma分布的推导，这里只是提供了一个笼统的思维框架。放在具体问题，需要：统计实验数据，并估计概率模型→基于合理的概率模型，得到用来增强的估计器。

三、最大后验估计 MAXIMUM a POStErIOrI (MAP) ESTIMATORS

　　A-幅值、相位估计器

准则函数

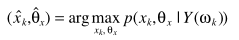
利用贝叶斯准则

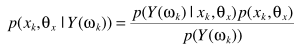
分母不影响参数的估计，忽略

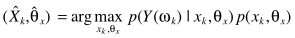
约束来了：1）DFT系数实部、虚部都是高斯分布;2）二者统计独立，从而有

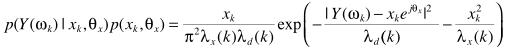
这样一来，求解就容易了

偏导为零，得出估计器

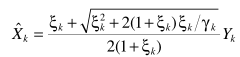
实际应用中具体参数的估计，与上面的思路都是一致的。

　　B-幅值估计器

只估计幅值：

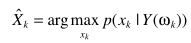
贝叶斯准则

忽略分母

利用

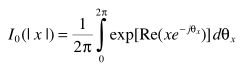
并借助A中的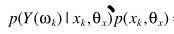两个表达式，得出估计

其中

与ML准则估计器中的思路一样，对Bessel近似处理

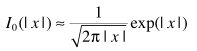
得出

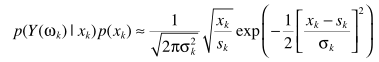
从而得出估计器

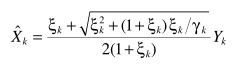
　　C-调参的建议

这一节是看到这里想到的，注意观察A、B两个估计器

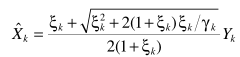
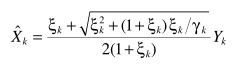
自己突发奇想，估计最多就水个水论文用得上，放在这里-感兴趣拿走。所以一个自然的思路是将他们推而广之：

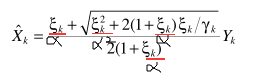
α是可以调节的参数。

ML、MMSE、MAP三种估计器：

1）其实ML可以理解成均匀分布的贝叶斯，这个时候的先验知识为零，通常贝叶斯假设高斯、拉普拉斯等分布（如幅值）,这就引入了先验知识，如果这个先验知识有效，理论上效果应该比ML更好;这就像回归中的应用：无约束=均匀分布→最小二乘，高斯分布→Ridge回归，拉普拉斯分布→Lasso回归。

2）MMSE是基于统计平均的贝叶斯估计，注意它与Wiener是有区别的，虽然都基于均方误差最小准则;

3）MMSE找的是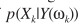的均值，即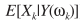，而MAP准则找的是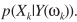的最大值。

四、利用不存在概率  INCORPORATING SPEECH ABSENCE PROBABILITY IN SPEECH ENHANCEMENT

其实就是信息融合，也就是Boosting的思想：两个弱分类器，组合一个强分类器，两个弱增强器，组合一个强增强器。不多说了，不过书中将这点应用的还不够深入。

组合

关于此部分的更多内容参考这里。