贝塞尔（Bezier） 曲线 研究

贝塞尔曲线最近经常接触到，今天研究了一下。

• 原理

关于它的原理，网上有很多。

1.一阶

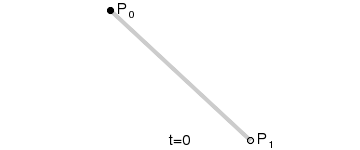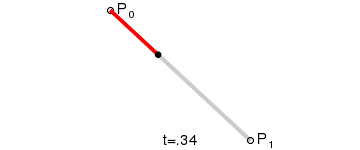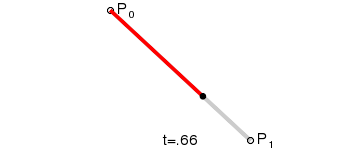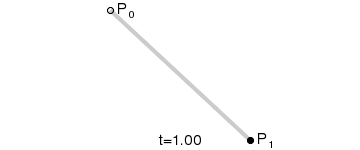
2.二阶

3.多阶

可以看到，多阶可以慢慢降阶为一阶贝塞尔曲线。

  //一阶
     private Vector3 BaseBezier(float t,Vector3 pos0,Vector3 pos1)
     {
         return pos0 + t * (pos1-pos0);
     }

递归，降阶为一阶

  //n阶
     private Vector3 BezierPro(float t,params Vector3[] posArray)
     {
         int l = posArray.Length;

         if (l<)
         {
             return Vector3.zero;
         }
         else  if (l == )
         {
             return BaseBezier(t, posArray[], posArray[]);
         }
         else
         {
             Vector3[] tempArray = new Vector3[l-];
             for (int i = ; i < l-; i++)
             {
                 tempArray[i] = BaseBezier(t, posArray[i], posArray[i + ]);
             }
             return BezierPro(t,tempArray);
         }

     }

　　在unity里整合：

 using UnityEngine;
 using System.Collections;
 using System.Linq;
 [ExecuteInEditMode]
 public class Bezier : MonoBehaviour {
     public LineRenderer line;
     public Transform[] PosArray;

     [Range(,)]
     public int sampleCount;
     // Use this for initialization
     void Start () {

     }

     // Update is called once per frame
     void Update () {
         SetBezier();
     }

     //一阶
     private Vector3 BaseBezier(float t,Vector3 pos0,Vector3 pos1)
     {
         return pos0 + t * (pos1-pos0);
     }
     //n阶
     private Vector3 BezierPro(float t,params Vector3[] posArray)
     {
         int l = posArray.Length;

         if (l<)
         {
             return Vector3.zero;
         }
         else  if (l == )
         {
             return BaseBezier(t, posArray[], posArray[]);
         }
         else
         {
             Vector3[] tempArray = new Vector3[l-];
             for (int i = ; i < l-; i++)
             {
                 tempArray[i] = BaseBezier(t, posArray[i], posArray[i + ]);
             }
             return BezierPro(t,tempArray);
         }

     }

     [ContextMenu("设置贝塞尔曲线")]
     private void SetBezier()
     {
         if (PosArray.Length<)
         {
             return;
         }
         Vector3[] tempArray = new Vector3[PosArray.Length];

         for (int i = ; i < PosArray.Length; i++)
         {
             tempArray[i] = PosArray[i].position;
         }

         line.SetVertexCount(sampleCount);
         for (int i = ; i < sampleCount; i++)
         {
             line.SetPosition(i, BezierPro( (float)i/(float)sampleCount, tempArray) );
         }
     }
 }

效果展示