PAT 甲级 1066 Root of AVL Tree (25 分)(快速掌握平衡二叉树的旋转,内含代码和注解)***

1066 Root of AVL Tree (25 分)

 

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

 

 

Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤) which is the total number of keys to be inserted. Then Ndistinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

70

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

88

题意：

将输入调整为平衡二叉树（AVL），输出根结点元素

题解：

判断插入结点对现有结点的平衡因子的影响，进而进行LL，LR，RL，RR旋转
假设三个结点连接关系为A->B->C,C为新插入结点并使得A的平衡因子==2
若C在A的左孩子的左子树上，则对A与B进行LL旋转
若C在A的左孩子的右子树上，则对A，B，C进行LR旋转，可分解为首先对B与C进行RR旋转，再对A与C进行LL旋转
若C在A的右孩子的右子树上，则对A与B进行RR旋转
若C在A的右孩子的左子树上，则对A，B，C进行RL旋转，可分解为首先对B与C进行LL旋转，再对A与C进行RR旋转

平衡二叉树选择详解:

4种平衡调整如下(结点的数字仅作标记作用)：

(图中数字仅用于区分节点的不同，不用来表示节点的数值大小)

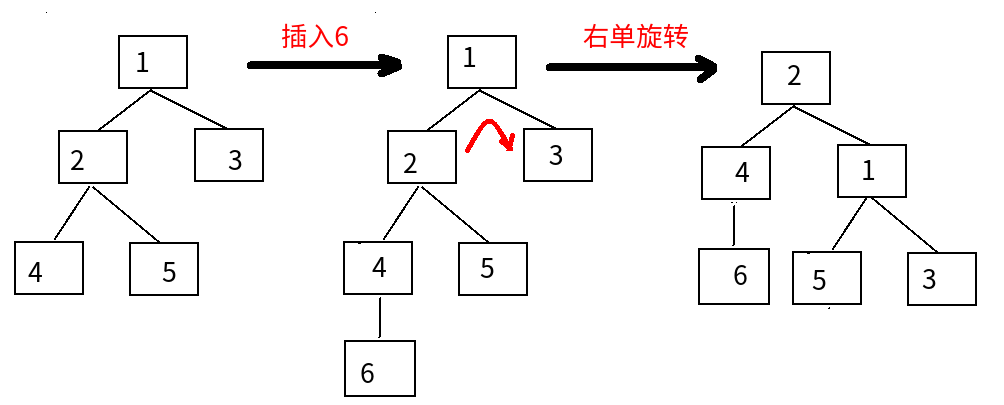
①LL：

对于根节点：左边比右边多

对于左节点：左边比右边多

右单旋转

　　

②RR：

对于根节点：右边比左边多

对于右节点：右边比左边多

左单旋转

　　

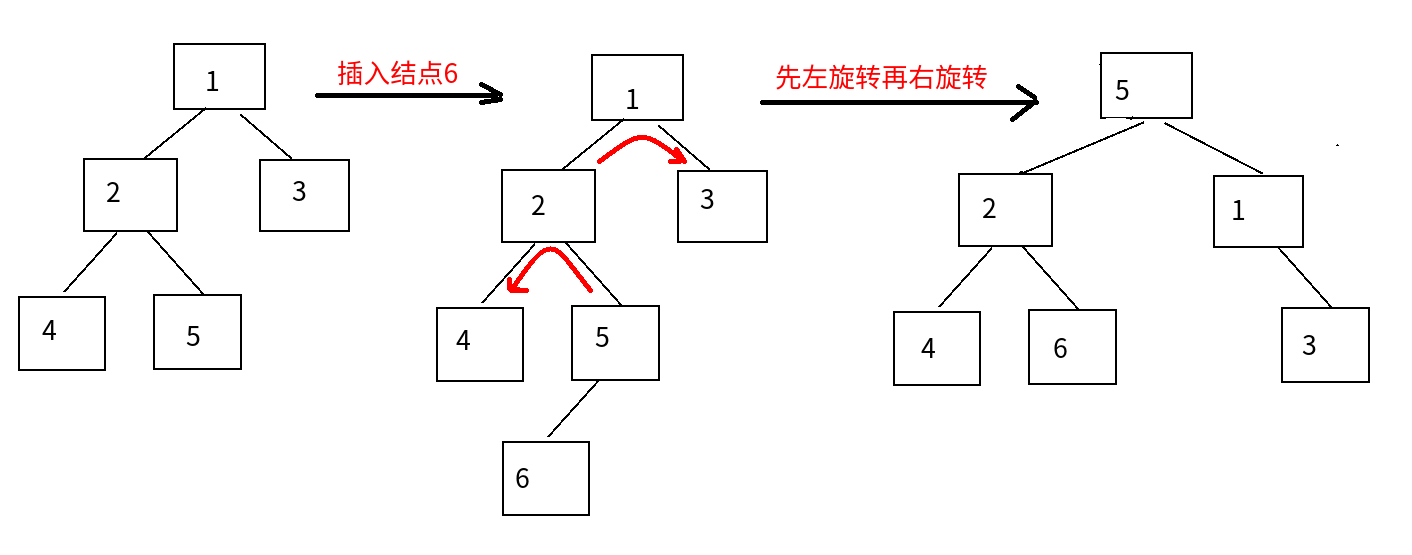
③LR平衡旋转：

对于根节点：左边比右边多

对于左节点：右边比左边多

先左后右(先处理左节点，再处理根节点)

　　

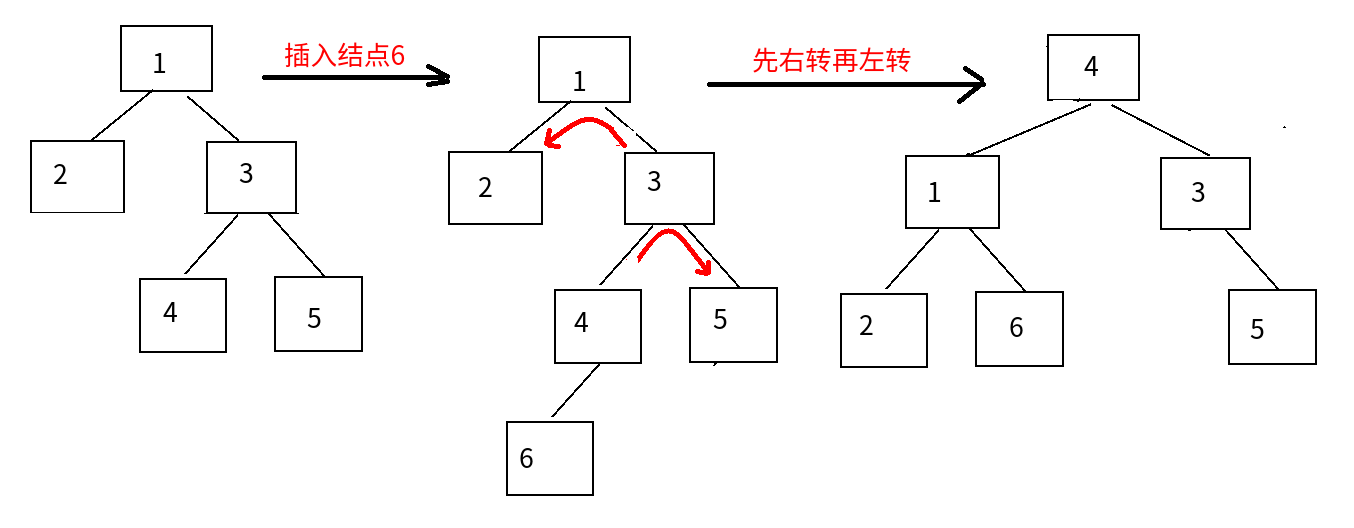
④RL平衡旋转：

对于根节点：右边比左边多

对于右节点：左边比右边多

先右后左(先处理右节点，再处理根节点)

　　

AC代码：

#include<iostream>
#include<algorithm>
using namespace std;
int n;
struct node{
    int data;
    node *lchild,*rchild;
};
node *Newnode(int x){//新建一个结点
    node* newnode=new node;
    newnode->data=x;
    newnode->lchild=newnode->rchild=NULL;
    return newnode;
}
int Height(node* root){//返回高度
    if(root==NULL) return ;
    else return max(Height(root->lchild),Height(root->rchild))+;
}
int getbalance(node* root){//检查是否平衡
    return Height(root->lchild)-Height(root->rchild);
}
void R(node*&root){//右旋
    //左节点成为根节点
    node* temp=root->lchild;
    root->lchild=root->rchild;//根的左边换成了左节点的右节点
    temp->rchild=root;//根自己成为了原来左节点的右节点
    root=temp;
}
void L(node*&root){//左旋
    //右节点成为根节点
    node *temp=root->rchild;
    root->rchild=temp->lchild;//根的右边换成了右节点的左节点
    temp->lchild=root;//根自己成为了原来右节点的左节点
    root=temp;
}
void insert(node*&root,int x){
    if(root==NULL){
        root=Newnode(x);
        return;
    }
    if(x<root->data){
        insert(root->lchild,x);
        if(getbalance(root)==){//左边必比右边高2
            if(getbalance(root->lchild)==){//左节点的左边比右边高1
                R(root);//右单旋
            }else if(getbalance(root->lchild)==-){//左节点的右边比左边高1
                L(root->lchild);//对于左节点左旋
                R(root);//再跟节点右旋
            }
        }
    }else{
        insert(root->rchild,x);
        if(getbalance(root)==-){//右边必比左边高2
            if(getbalance(root->rchild)==){//右节点的左边比右边高1
                R(root->rchild);//对于右节点右旋
                L(root);//再跟节点左旋
            }else if(getbalance(root->rchild)==-){//右节点的右边比左边高1
                L(root);//左单旋
            }
        }
    }
}
int main(){
    scanf("%d",&n);
    node *root = NULL;
    for(int i=;i<n;i++){
        int x;
        scanf("%d",&x);
        insert(root,x);
    }
    printf("%d",root->data);//输出处理好的平衡二叉树的根节点
    return ;
}