Canvas：绘制多边形

前言

CanvasRenderingContext2D 没有提供绘制多边形的函数，所以只能由我们自己来实现绘制多边形的函数。以六边形为基础，需要用到三角函数：sin 和 cos。

点 A 坐标

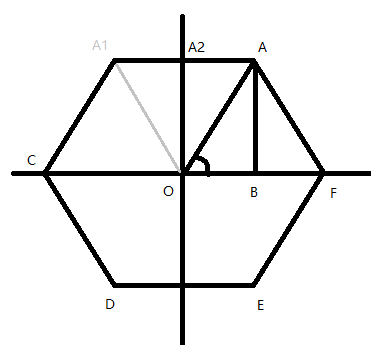
（一）连接必要的辅助线：①连接点 A 和点 O；②从点 A 往下作一条垂直线；③连接点 A₁ 和点 O。（二）已知的量：①AO 实际就是圆 O 的半径。点 A 坐标的求解步骤：

1. 求 ∠AOB；
2. 求 OB 的长；
3. 求 AB 的长；
4. X 轴上的坐标：O 的 X 轴 + OB 的长度；
5. Y 轴上的坐标：O 的 Y 轴 - AB 的长度；

求 A 点的坐标就必须要知道 OB 和 AB。

求 OB 的长

领边比斜边用 COS 函数，那么 OB 的长就是：

\[cos∠AOB = \frac{OB}{AO}
\]

求 AB 的长

对边比斜边用 SIN 函数，那么 AB 的长就是：

\[sin∠AOB = \frac{AB}{AO}
\]

求 ∠AOB

求 OB 和 AB 就必须要知道 ∠AOB。观察可知，∠AOB 的度数是360° / 6 = 60°。

代码实现

let circX = 100, circY = 100, // 圆心坐标
let sides = 6, angleAOB = (Math.PI * 2) / sides; // ∠AOB

let sideOB = Math.cos(angleAOB) * radius, sideAB = Math.sin(angleAOB) * radius;

let aX = circX + sideOB, // 点 A 的 x 坐标
let aY = circY - sideAB; // 点 A 的 y 坐标

所以最终求得点 A 的坐标：(140, 30.717967697244916)。

点 F 坐标

点 F 不能直接构成一个三角形，所以度数是 0°。sin0° = 0、cos0°= 1：

let circX = 100, circY = 100, // 圆心坐标
let sides = 6, angle = 0;

let adjacentSide = Math.cos(angle) * radius, beveledSide = Math.sin(angle) * radius;

let aX = circX + adjacentSide, // 点 F 的 x 坐标
let aY = circY - beveledSide; // 点 F 的 y 坐标

所以最终求得点 F 的坐标：(180, 100)。

求所有点坐标

通过上面两个坐标的求解过程可知，只有三角形的度数在增加，从点 F 顺时针开始，每一个角是自身的角度再加 60°。

let radius = 80, sides = 6, circX = 100, circY = 100;
let angle = (Math.PI * 2) / sides, accumulator = 0;

for ( let i = 0; i < sides; i++ ) {
	let adjacentSide = Math.cos(accumulator) * radius;
	let beveledSide = Math.sin(accumulator) * radius;
	let aX = circX + adjacentSide;
	let aY = circY - beveledSide;
	ctx.lineTo(aX, aY);
	accumulator += angle;
}

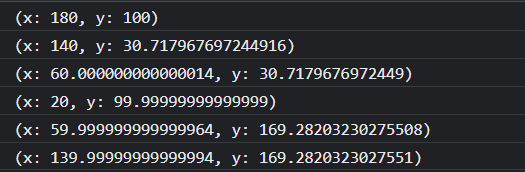
6 个点坐标的结果依次是：

封装成函数

只需提供多边形有多少面、多边形的圆心半径：

function drawPolygonPath(sides, radius, circX, circY, ctx) {
	let angle = (Math.PI * 2) / sides, accumulator = 0;

	ctx.beginPath();
	for ( let i = 0; i < sides; i++ ) {
		let adjacentSide = Math.cos(accumulator) * radius;
		let beveledSide = Math.sin(accumulator) * radius;
		let aX = circX + adjacentSide;
		let aY = circY - beveledSide;
		ctx.lineTo(aX, aY);
		accumulator += angle;
	}
	ctx.closePath();
	ctx.stroke();
}

ctx.lineTo(aX, aY) 确定多边形所有的点，在循环结束之后关闭路径，再调用ctx.stroke() 函数，完成多边形的绘制。

let canvas = document.getElementById("canvas");
let ctx = canvas.getContext("2d");

drawPolygonPath(6, 80, 100, 100, ctx);