Scrambled Polygon(斜率排序)

Scrambled Polygon

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 7799		Accepted: 3707

Description

A closed polygon is a figure bounded by a finite number of line segments. The intersections of the bounding line segments are called the vertices of the polygon. When one starts at any vertex of a closed polygon and traverses each bounding line segment exactly once, one comes back to the starting vertex. 
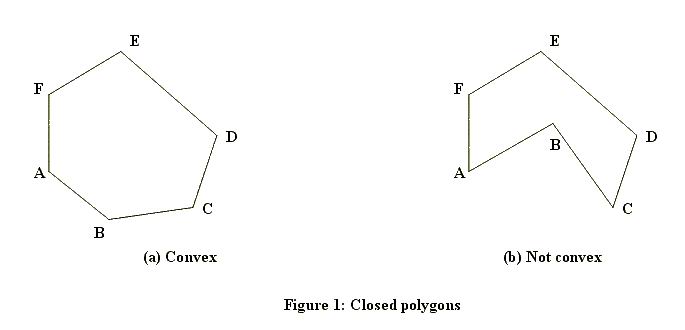
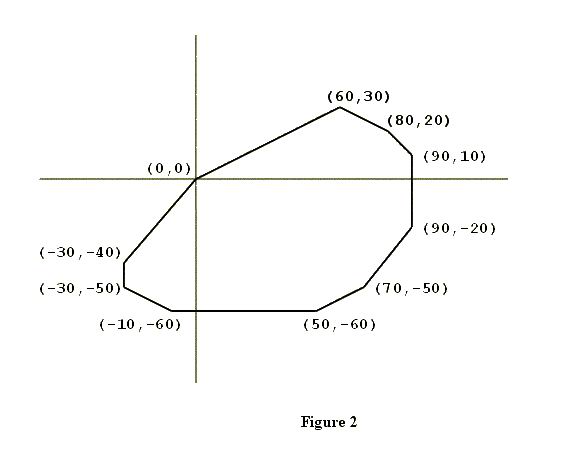
A closed polygon is called convex if the line segment joining any two points of the polygon lies in the polygon. Figure 1 shows a closed polygon which is convex and one which is not convex. (Informally, a closed polygon is convex if its border doesn't have any "dents".) The subject of this problem is a closed convex polygon in the coordinate plane, one of whose vertices is the origin (x = 0, y = 0). Figure 2 shows an example. Such a polygon will have two properties significant for this problem. 
The first property is that the vertices of the polygon will be confined to three or fewer of the four quadrants of the coordinate plane. In the example shown in Figure 2, none of the vertices are in the second quadrant (where x < 0, y > 0). 
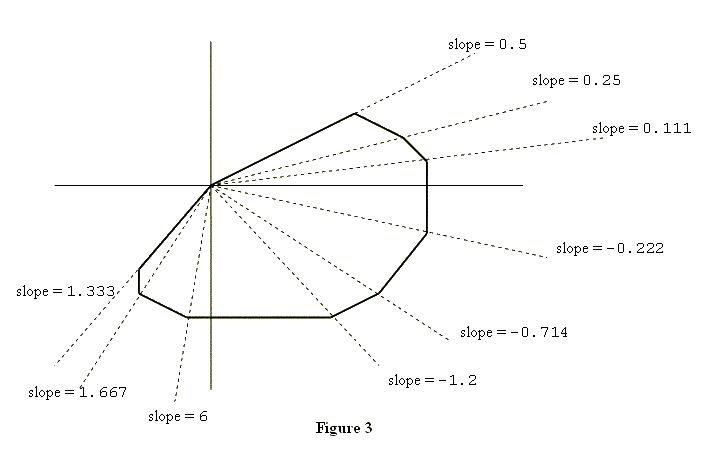
To describe the second property, suppose you "take a trip" around the polygon: start at (0, 0), visit all other vertices exactly once, and arrive at (0, 0). As you visit each vertex (other than (0, 0)), draw the diagonal that connects the current vertex with (0, 0), and calculate the slope of this diagonal. Then, within each quadrant, the slopes of these diagonals will form a decreasing or increasing sequence of numbers, i.e., they will be sorted. Figure 3 illustrates this point.  

Input

The input lists the vertices of a closed convex polygon in the plane. The number of lines in the input will be at least three but no more than 50. Each line contains the x and y coordinates of one vertex. Each x and y coordinate is an integer in the range -999..999. The vertex on the first line of the input file will be the origin, i.e., x = 0 and y = 0. Otherwise, the vertices may be in a scrambled order. Except for the origin, no vertex will be on the x-axis or the y-axis. No three vertices are colinear.

Output

The output lists the vertices of the given polygon, one vertex per line. Each vertex from the input appears exactly once in the output. The origin (0,0) is the vertex on the first line of the output. The order of vertices in the output will determine a trip taken along the polygon's border, in the counterclockwise direction. The output format for each vertex is (x,y) as shown below.

Sample Input

0 0
70 -50
60 30
-30 -50
80 20
50 -60
90 -20
-30 -40
-10 -60
90 10

Sample Output

(0,0)
(-30,-40)
(-30,-50)
(-10,-60)
(50,-60)
(70,-50)
(90,-20)
(90,10)
(80,20)
(60,30)
题意：给你一系列点，让输出一个凸多边形的各点，把斜率从大到小排序就好了；
代码;

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
const int INF=0x3f3f3f3f;
#define mem(x,y) memset(x,y,sizeof(x))
#define SI(x) scanf("%d",&x);
struct Node{
	int x,y;
	/*friend bool operator < (Node a,Node b){
		if(a.x!=b.x)return a.x<b.x;
		else return a.y<b.y;
	}*/
}dt[100010];
int cross(Node a,Node b){
	return a.x*b.y-a.y*b.x;
}
int cmp(Node a,Node b){
		if(cross(a,b)>0)return 1;
		else return 0;
	}
int main(){
	int k=0;
	while(~scanf("%d%d",&dt[k].x,&dt[k].y))k++;
	sort(dt+1,dt+k,cmp);
	for(int i=0;i<k;i++)printf("(%d,%d)\n",dt[i].x,dt[i].y);
	return 0;
}