【BZOJ 2007】 2007: [Noi2010]海拔 (平面图转对偶图+spfa)
2007: [Noi2010]海拔
Time Limit: 20 Sec Memory Limit: 552 MB
Submit: 2504 Solved: 1195Description
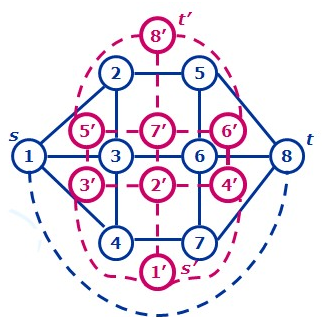
YT市是一个规划良好的城市,城市被东西向和南北向的主干道划分为n×n个区域。简单起见,可以将YT市看作一个正方形,每一个区域也可看作一个正方形。从而,YT城市中包括(n+1)×(n+1)个交叉路口和2n×(n+1)条双向道路(简称道路),每条双向道路连接主干道上两个相邻的交叉路口。下图为一张YT市的地图(n = 2),城市被划分为2×2个区域,包括3×3个交叉路口和12条双向道路。 小Z作为该市的市长,他根据统计信息得到了每天上班高峰期间YT市每条道路两个方向的人流量,即在高峰期间沿着该方向通过这条道路的人数。每一个交叉路口都有不同的海拔高度值,YT市市民认为爬坡是一件非常累的事情,每向上爬h的高度,就需要消耗h的体力。如果是下坡的话,则不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为h(注意h可能是负数),那么一个人经过这段路所消耗的体力是max{0, h}(这里max{a, b}表示取a, b两个值中的较大值)。 小Z还测量得到这个城市西北角的交叉路口海拔为0,东南角的交叉路口海拔为1(如上图所示),但其它交叉路口的海拔高度都无法得知。小Z想知道在最理想的情况下(即你可以任意假设其他路口的海拔高度),每天上班高峰期间所有人爬坡所消耗的总体力和的最小值。Input
第一行包含一个整数n,含义如上文所示。接下来4n(n + 1)行,每行包含一个非负整数分别表示每一条道路每一个方向的人流量信息。输入顺序:n(n + 1)个数表示所有从西到东方向的人流量,然后n(n + 1)个数表示所有从北到南方向的人流量,n(n + 1)个数表示所有从东到西方向的人流量,最后是n(n + 1)个数表示所有从南到北方向的人流量。对于每一个方向,输入顺序按照起点由北向南,若南北方向相同时由西到东的顺序给出(参见样例输入)。Output
仅包含一个数,表示在最理想情况下每天上班高峰期间所有人爬坡所消耗的总体力和(即总体力和的最小值),结果四舍五入到整数。Sample Input
1
1
2
3
4
5
6
7
8Sample Output
3【样例说明】
样例数据见下图。最理想情况下所有点的海拔如上图所示。
对于100%的数据:1 ≤ n ≤ 500,0 ≤ 流量 ≤ 1,000,000且所有流量均为整数。HINT
Source
【分析】
跟狼抓兔子差不多?
首先,大胆地考虑一下只有1和0?【如果不是,你可以假设一下只有一个点不是,周围都是,然后往好的地方修改,至少不会变差的】
当然你也不会无聊到1,0,1,0,交替。。不然累死人【其实最好就是都是平的,但是规定了两个角是有高度差的】
所以只要找到0,1分界线,就变成了最小割了。
但这种图嘛,可以转化成成对偶图,跑最短路就好了【别人说卡spfa?但是我过了】
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
#define Maxn 510 int num[Maxn][Maxn],cnt; struct node
{
int x,y,c,next;
}t[Maxn*Maxn*];
int first[Maxn*Maxn*],len;
void ins(int x,int y,int c)
{
// printf("%d -> %d %d\n",x,y,c);
t[++len].x=x;t[len].y=y;t[len].c=c;
t[len].next=first[x];first[x]=len;
} queue<int > q;
bool inq[Maxn*Maxn*];
int dis[Maxn*Maxn*],st,ed;
bool spfa()
{
while(!q.empty()) q.pop();
memset(inq,,sizeof(inq));
for(int i=;i<=ed;i++) dis[i]=-;
inq[st]=;dis[st]=;
q.push(st);
while(!q.empty())
{
int x=q.front();
for(int i=first[x];i;i=t[i].next)
{
int y=t[i].y;
if(dis[y]==-||dis[y]>dis[x]+t[i].c)
{
dis[y]=dis[x]+t[i].c;
if(!inq[y])
{
q.push(y);
inq[y]=;
}
}
}q.pop();inq[x]=;
}
if(dis[ed]==-) return ;
return ;
} int main()
{
int n;
scanf("%d",&n);
for(int i=;i<=n;i++)
for(int j=;j<=n;j++) num[i][j]=++cnt;
for(int i=;i<=n;i++) num[i][]=cnt+;
for(int i=;i<=n;i++) num[n+][i]=cnt+;
len=;
memset(first,,sizeof(first));
for(int i=;i<=n+;i++)
for(int j=;j<=n;j++)
{
int x;scanf("%d",&x);
ins(num[i-][j],num[i][j],x);
}
for(int i=;i<=n;i++)
for(int j=;j<=n+;j++)
{
int x;scanf("%d",&x);
ins(num[i][j],num[i][j-],x);
}
for(int i=;i<=n+;i++)
for(int j=;j<=n;j++)
{
int x;scanf("%d",&x);
ins(num[i][j],num[i-][j],x);
}
for(int i=;i<=n;i++)
for(int j=;j<=n+;j++)
{
int x;scanf("%d",&x);
ins(num[i][j-],num[i][j],x);
}
st=;ed=cnt+;
// st=cnt+1;ed=0;
spfa();
printf("%d\n",dis[ed]);
return ;
}
2017-03-29 08:11:42
平面图转对偶图总结:
转自:http://blog.sina.com.cn/s/blog_60707c0f01011fnn.html
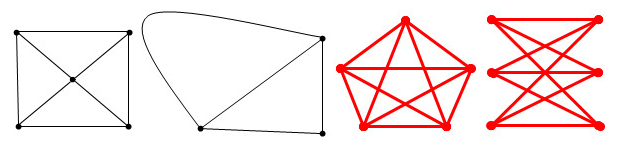
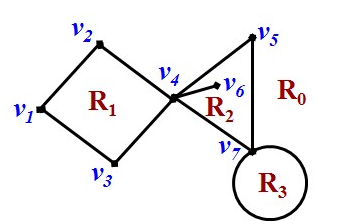
利用欧拉公式和数学归纳法可以证明平面图G的所有面的度之和等于其边数|E|的2倍,即:
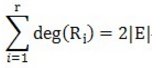
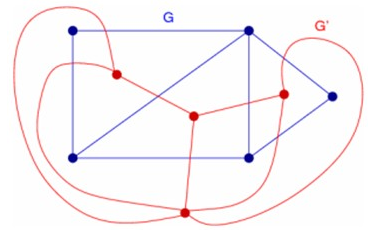
1 最大流的应用
【BZOJ 2007】 2007: [Noi2010]海拔 (平面图转对偶图+spfa)的更多相关文章
- BZOJ2007 NOI2010 海拔 平面图转对偶图 最小割
题面太长啦,请诸位自行品尝—>海拔 分析: 这是我见过算法比较明显的最小割题目了,很明显对于某一条简单路径,海拔只会有一次变换. 而且我们要最终使变换海拔的边权值和最小. 我们发现变换海拔相当于 ...
- [NOI2010]海拔 平面图转对偶图 最小割
题解: 首先,我们不难猜到高度只有 $0$ 或 $1$ 两种可能,而且高度为 0 的地区组成一个联通块,高度为 1 的地区组成一个联通块.只有这样,人们所耗费的体力才是最小的.得出这个结论,题目就成了 ...
- P2046 [NOI2010]海拔 平面图转对偶图(最小割-》最短路)
$ \color{#0066ff}{ 题目描述 }$ YT市是一个规划良好的城市,城市被东西向和南北向的主干道划分为n×n个区域.简单起见,可以将YT市看作 一个正方形,每一个区域也可看作一个正方形. ...
- Vijos1734 NOI2010 海拔 平面图最小割
建立平面图的对偶图,把最小割转化成最短路问题 Dijkstra算法堆优化 (被输入顺序搞WA了好几次T_T) #include <cstdio> #include <cstring& ...
- bzoj 4541: [Hnoi2016]矿区【平面图转对偶图+生成树】
首先平面图转对偶图,大概思路是每条边存正反,每个点存出边按极角排序,然后找每条边在它到达点的出边中极角排序的下一个,这样一定是这条边所属最小多边形的临边,然后根据next边找出所有多边形,用三角剖分计 ...
- BZOJ.2007.[NOI2010]海拔(最小割 对偶图最短路)
题目链接 想一下能猜出,最优解中海拔只有0和1,且海拔相同的点都在且只在1个连通块中. 这就是个平面图最小割.也可以转必须转对偶图最短路,不然只能T到90分了..边的方向看着定就行. 不能忽略回去的边 ...
- Luogu2046 NOI2010 海拔 平面图、最小割、最短路
传送门 首先一个不知道怎么证的结论:任意点的\(H\)只会是\(0\)或\(1\) 那么可以发现原题的本质就是一个最小割,左上角为\(S\),右下角为\(T\),被割开的两个部分就是\(H=0\)与\ ...
- 【bzoj2007】[Noi2010]海拔 最小割+对偶图+最短路
题目描述 YT市是一个规划良好的城市,城市被东西向和南北向的主干道划分为n×n个区域.简单起见,可以将YT市看作一个正方形,每一个区域也可看作一个正方形.从而,YT城市中包括(n+1)×(n+1)个交 ...
- NOI 2010 海拔 ——平面图转对偶图
[题目分析] 可以知道,所有的海拔是0或1 最小割转最短路,就可以啦 SPFA被卡,只能换DIJ [代码] #include <cstdio> #include <cstring&g ...
随机推荐
- 《JavaScript 实战》:JavaScript 图片滑动切换效果
看到alibaba的一个图片切换效果,感觉不错,想拿来用用.但代码一大堆的,看着昏,还是自己来吧.由于有了做图片滑动展示效果的经验,做这个就容易得多了. 效果预览 仿淘宝/alibaba图片切换: 默 ...
- 【Hadoop】用web查看hadoop运行状态
博文已转移,请借一步说话.http://www.daniubiji.cn/archives/621 上一篇文章(去博客园),我们安装完hadoop,下面我们从视觉上看看hadoop怎么玩的. 我们可以 ...
- 【洛谷 P4291】 [HAOI2008]排名系统(Splay,Trie)
题目链接 不是双倍经验我会去\(debug\)一上午? 一开始我是用的\(map+string\),跑的太慢了,T了4个点. 后来我手写了\(string\),重载了小于号,依然用的\(map\),T ...
- 【leetcode 简单】第十三题 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和. 示例: 输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6 解释: 连续子数组 ...
- Count on a tree(SPOJ COT + 树上第k大 + 主席树 + LCA)
题目链接:https://www.spoj.com/problems/COT/en/ 题目: 题意: 给你一棵有n个节点的树,求节点u到节点v这条链上的第k大. 思路: 我们首先用dfs进行建题目给的 ...
- A .Gaby And Addition (Gym - 101466A + 字典树)
题目链接:http://codeforces.com/gym/101466/problem/A 题目: 题意: 给你n个数,重定义两个数之间的加法不进位,求这些数中两个数相加的最大值和最小值. 思路: ...
- 39、请用代码简答实现stack
栈和队列是两种基本的数据结构,同为容器类型.两者根本的区别在于: stack:后进先出 queue:先进先出 PS:stack和queue是不能通过查询具体某一个位置的元素而进行操作的.但是他们的排列 ...
- HTML如何编写为桌面程序
学过/用过HTML的人应该都知道HTML是标记语言,是在网页上执行/使用的,在这里小编告诉你HTML也可以用来做桌面程序,这种桌面程序一般是微客户端 工具/原料 html dreamweaver ...
- 64_p1
PEGTL-devel-1.3.1-2.fc26.i686.rpm 13-Feb-2017 22:10 64086 PEGTL-devel-1.3.1-2.fc26.x86_64.rpm 13-Feb ...
- Delphi 10 seattle 去掉自带的代码连接线
