《DSP using MATLAB》Problem 7.30


代码:
%% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
%% Output Info about this m-file
fprintf('\n***********************************************************\n');
fprintf(' <DSP using MATLAB> Problem 7.30 \n\n'); banner();
%% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ % bandstop, Length MUST be odd number.
wp1 = 0.3*pi; ws1 = 0.4*pi; ws2 = 0.6*pi; wp2 = 0.7*pi;
As = 50; Rp = 0.2; [delta1, delta2] = db2delta(Rp, As);
deltaH = max(delta1,delta2); deltaL = min(delta1,delta2); f = [wp1, ws1, ws2, wp2]/pi; m = [1, 0, 1]; delta = [delta1, delta2, delta1]; [N, f, m, weights] = firpmord(f, m, delta);
N h = firpm(N, f, m, weights);
[db, mag, pha, grd, w] = freqz_m(h, [1]);
delta_w = 2*pi/1000;
wp1i = floor(wp1/delta_w)+1; ws1i = floor(ws1/delta_w)+1;
ws2i = floor(ws2/delta_w)+1; wp2i = floor(wp2/delta_w)+1; Asd = -max(db(ws1i : 1 : ws2i)) M = N + 1
l = 0:M-1;
%% --------------------------------------------------
%% Type-1 BPF
%% --------------------------------------------------
[Hr, ww, a, L] = Hr_Type1(h); Rp = -(min(db(1:1: wp1i))); % Actual Passband Ripple
fprintf('\nActual Passband Ripple is %.4f dB.\n', Rp); As = -round(max(db(ws1i : 1 : ws2i))); % Min Stopband attenuation
fprintf('\nMin Stopband attenuation is %.4f dB.\n', As); [delta1_db, delta2_db] = db2delta(Rp, As) % Plot
figure('NumberTitle', 'off', 'Name', 'Problem 7.30 h(n), Parks-McClellan Method')
set(gcf,'Color','white');
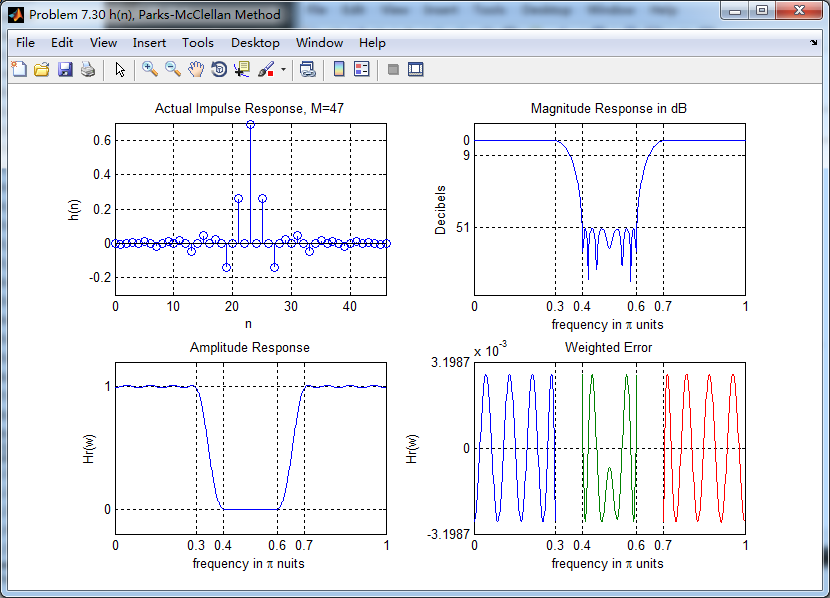
subplot(2,2,1); stem([0:M-1], h); axis([0 M-1 -0.3 0.7]); grid on;
xlabel('n'); ylabel('h(n)'); title('Actual Impulse Response, M=47'); subplot(2,2,2); plot(w/pi, db); axis([0 1 -90 10]); grid on;
set(gca,'YTickMode','manual','YTick',[-51,-9,0])
set(gca,'YTickLabelMode','manual','YTickLabel',['51';' 9';' 0']);
set(gca,'XTickMode','manual','XTick',[0,0.3,0.4,0.6,0.7,1]);
xlabel('frequency in \pi units'); ylabel('Decibels'); title('Magnitude Response in dB'); subplot(2,2,3); plot(ww/pi, Hr); axis([0, 1, -0.2, 1.2]); grid on;
xlabel('frequency in \pi nuits'); ylabel('Hr(w)'); title('Amplitude Response');
set(gca,'XTickMode','manual','XTick',[0,0.3,0.4,0.6,0.7,1])
set(gca,'YTickMode','manual','YTick',[0,1]); subplot(2,2,4);
pb1w = ww(1:1:wp1i)/pi; pb1e = Hr(1:1:wp1i)-1;
sbw = ww(ws1i:ws2i)/pi; sbe = Hr(ws1i:ws2i);
pb2w = ww(wp2i:501)/pi; pb2e = Hr(wp2i:501)-1;
plot(pb1w,pb1e*(delta2/delta1), sbw,sbe, pb2w,pb2e*(delta2/delta1)); % weighted error
% plot(pb1w,pb1e, sbw,sbe, pb2w,pb2e); % error axis([0, 1, -deltaL, deltaL]); grid on;
xlabel('frequency in \pi units'); ylabel('Hr(w)');
title('Weighted Error');
%title('Error Response');
set(gca,'XTickMode','manual','XTick',f)
set(gca,'YTickMode','manual','YTick',[-deltaL, 0,deltaL]);
set(gca,'XGrid','on','YGrid','on') figure('NumberTitle', 'off', 'Name', 'Problem 7.30 Parks-McClellan Method')
set(gcf,'Color','white');
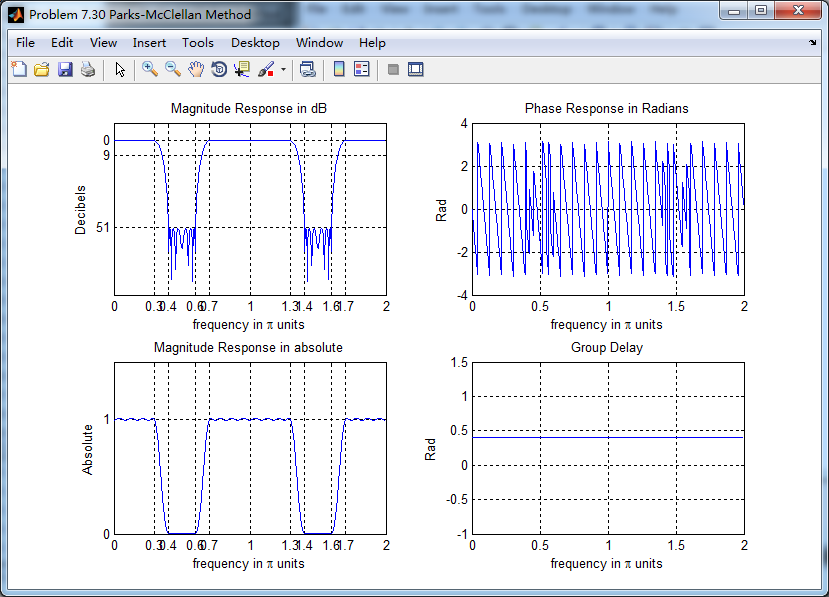
subplot(2,2,1); plot(w/pi, db); grid on; axis([0 2 -90 10]);
set(gca,'YTickMode','manual','YTick',[-51,-9,0])
set(gca,'YTickLabelMode','manual','YTickLabel',['51';' 9';' 0']);
set(gca,'XTickMode','manual','XTick',[0,0.3,0.4,0.6,0.7,1,1.3,1.4,1.6,1.7,2]);
xlabel('frequency in \pi units'); ylabel('Decibels'); title('Magnitude Response in dB'); subplot(2,2,3); plot(w/pi, mag); grid on; %axis([0 1 -100 10]);
xlabel('frequency in \pi units'); ylabel('Absolute'); title('Magnitude Response in absolute');
set(gca,'XTickMode','manual','XTick',[0,0.3,0.4,0.6,0.7,1,1.3,1.4,1.6,1.7,2]);
set(gca,'YTickMode','manual','YTick',[0,1.0]); subplot(2,2,2); plot(w/pi, pha); grid on; %axis([0 1 -100 10]);
xlabel('frequency in \pi units'); ylabel('Rad'); title('Phase Response in Radians');
subplot(2,2,4); plot(w/pi, grd*pi/180); grid on; %axis([0 1 -100 10]);
xlabel('frequency in \pi units'); ylabel('Rad'); title('Group Delay'); figure('NumberTitle', 'off', 'Name', 'Problem 7.30 AmpRes of h(n), Parks-McClellan Method')
set(gcf,'Color','white'); plot(ww/pi, Hr); grid on; %axis([0 1 -100 10]);
xlabel('frequency in \pi units'); ylabel('Hr'); title('Amplitude Response');
set(gca,'YTickMode','manual','YTick',[-delta2_db ,0,delta2_db , 1-delta1_db, 1, 1+delta1_db]);
set(gca,'XTickMode','manual','XTick',[0,0.3,0.4,0.6,0.7,1]); n = [0:1:300];
x = 5-5*cos(pi*n/2);
y = filter(h,1,x); figure('NumberTitle', 'off', 'Name', 'Problem 7.30 x(n) and y(n)')
set(gcf,'Color','white');
subplot(3,1,1); stem([0:M-1], h); axis([0 M-1 -0.3 0.7]); grid on;
xlabel('n'); ylabel('h(n)'); title('Actual Impulse Response, M=47'); subplot(3,1,2); stem(n, x); axis([0 300 0 10]); grid on;
xlabel('n'); ylabel('x(n)'); title('Input sequence'); subplot(3,1,3); stem(n, y); axis([0 100 -5 7]); grid on;
xlabel('n'); ylabel('y(n)'); title('Output sequence'); % ---------------------------
% DTFT of x
% ---------------------------
MM = 500;
[X, w1] = dtft1(x, n, MM);
[Y, w1] = dtft1(y, n, MM); magX = abs(X); angX = angle(X); realX = real(X); imagX = imag(X);
magY = abs(Y); angY = angle(Y); realY = real(Y); imagY = imag(Y); figure('NumberTitle', 'off', 'Name', 'Problem 7.30 DTFT of x(n)')
set(gcf,'Color','white');
subplot(2,2,1); plot(w1/pi,magX); grid on; %axis([0,2,0,15]);
title('Magnitude Part');
xlabel('frequency in \pi units'); ylabel('Magnitude |X|');
subplot(2,2,3); plot(w1/pi, angX/pi); grid on; axis([0,2,-1,1]);
title('Angle Part');
xlabel('frequency in \pi units'); ylabel('Radians/\pi'); subplot('2,2,2'); plot(w1/pi, realX); grid on;
title('Real Part');
xlabel('frequency in \pi units'); ylabel('Real');
subplot('2,2,4'); plot(w1/pi, imagX); grid on;
title('Imaginary Part');
xlabel('frequency in \pi units'); ylabel('Imaginary'); figure('NumberTitle', 'off', 'Name', 'Problem 7.30 DTFT of y(n)')
set(gcf,'Color','white');
subplot(2,2,1); plot(w1/pi,magY); grid on; %axis([0,2,0,15]);
title('Magnitude Part');
xlabel('frequency in \pi units'); ylabel('Magnitude |Y|');
subplot(2,2,3); plot(w1/pi, angY/pi); grid on; axis([0,2,-1,1]);
title('Angle Part');
xlabel('frequency in \pi units'); ylabel('Radians/\pi'); subplot('2,2,2'); plot(w1/pi, realY); grid on;
title('Real Part');
xlabel('frequency in \pi units'); ylabel('Real');
subplot('2,2,4'); plot(w1/pi, imagY); grid on;
title('Imaginary Part');
xlabel('frequency in \pi units'); ylabel('Imaginary'); figure('NumberTitle', 'off', 'Name', 'Problem 7.30 Magnitude Response')
set(gcf,'Color','white');
subplot(1,2,1); plot(w1/pi,magX); grid on; %axis([0,2,0,15]);
title('Magnitude Part of Input');
xlabel('frequency in \pi units'); ylabel('Magnitude |X|');
subplot(1,2,2); plot(w1/pi,magY); grid on; %axis([0,2,0,15]);
title('Magnitude Part of Output');
xlabel('frequency in \pi units'); ylabel('Magnitude |Y|');
运行结果:
滤波器长度M=47,阻带衰减满足设计指标。

幅度谱和相位谱
振幅谱,把阻带、通带放大,数数极值点的个数。
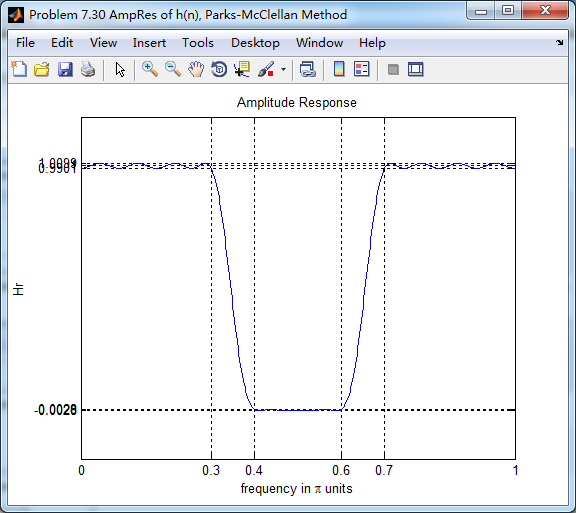
下图,9个极值点
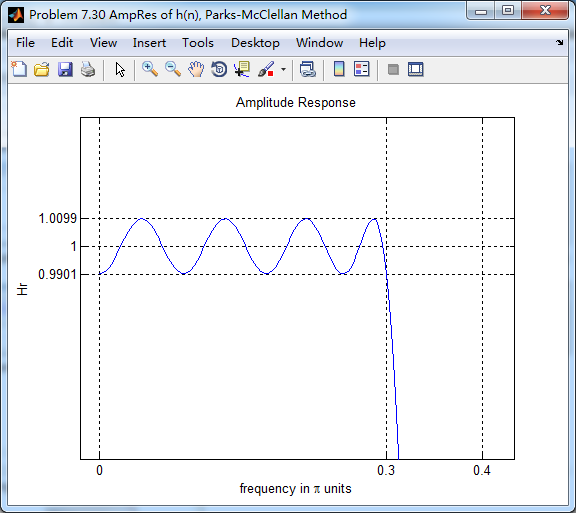
下图,8个极值点

下图,9个极值点

总共有9+8+9=26个极值点,M=47,L=(M-1)/2=23,0到π上,最多L+3=26个极值点。
输入输出序列

输入序列的谱,注意0.5π的频率分量,通过带阻滤波后消除了。
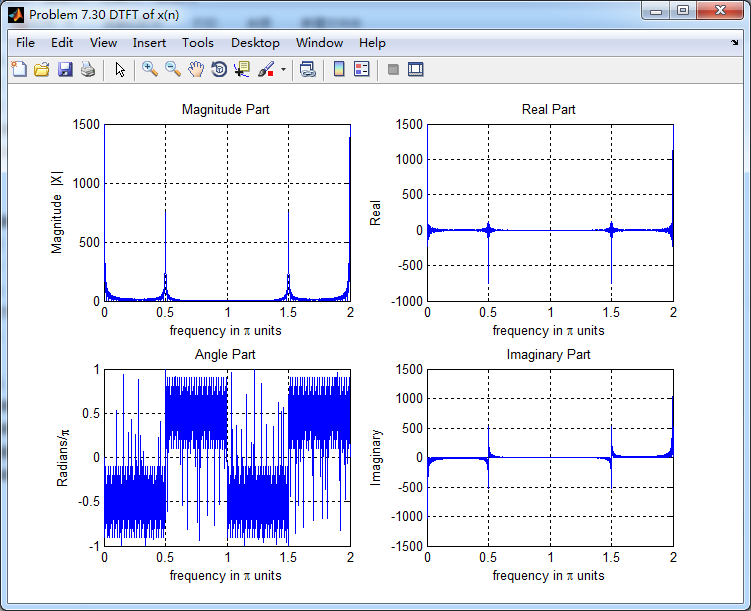
输出序列的谱,0.5π分量滤除了。
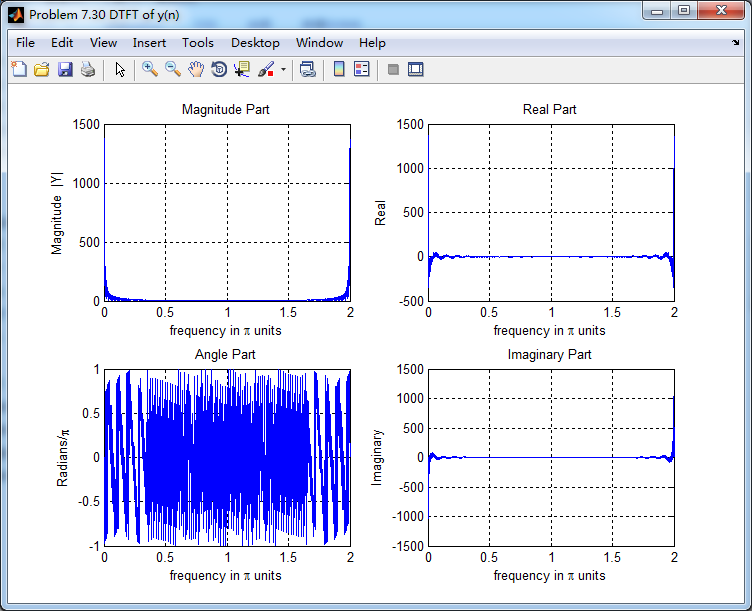
滤波前后幅度谱对比
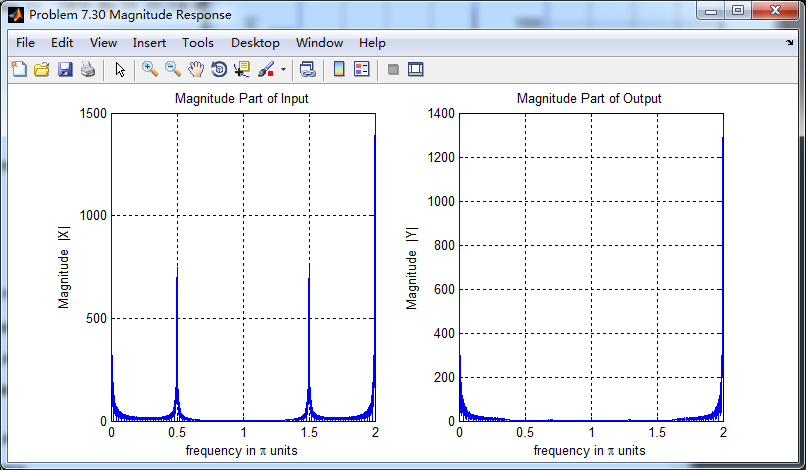
《DSP using MATLAB》Problem 7.30的更多相关文章
- 《DSP using MATLAB》Problem 8.30
10月1日,新中国70周岁生日,上午观看了盛大的庆祝仪式,整齐的方阵,先进的武器,尊敬的先辈英雄,欢乐的人们,愿我们的 国家越来越好,人民生活越来越好. 接着做题. 代码: %% ---------- ...
- 《DSP using MATLAB》Problem 5.30
代码: %% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ %% Output In ...
- 《DSP using MATLAB》Problem 7.23
%% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ %% Output Info a ...
- 《DSP using MATLAB》Problem 5.22
代码: %% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ %% O ...
- 《DSP using MATLAB》Problem 5.20
窗外的知了叽叽喳喳叫个不停,屋里温度应该有30°,伏天的日子难过啊! 频率域的方法来计算圆周移位 代码: 子函数的 function y = cirshftf(x, m, N) %% -------- ...
- 《DSP using MATLAB》Problem 3.8
2018年元旦,他乡加班中,外面尽是些放炮的,别人的繁华与我无关. 代码: %% ----------------------------------------------------------- ...
- 《DSP using MATLAB》Problem 3.3
按照题目的意思需要利用DTFT的性质,得到序列的DTFT结果(公式表示),本人数学功底太差,就不写了,直接用 书中的方法计算并画图. 代码: %% -------------------------- ...
- 《DSP using MATLAB》Problem 2.20
代码: %% ------------------------------------------------------------------------ %% Output Info about ...
- 《DSP using MATLAB》Problem 2.14
代码: %% ------------------------------------------------------------------------ %% Output Info about ...
随机推荐
- vue.js+web storm安装及第一个vue.js
小白还是自己写一遍吧 1.下载node.js https://nodejs.org/en/download/ 2.安装淘宝镜像(类似于阿里云的maven中央仓库镜像) 安装时间有点长 安装命令:npm ...
- AtCoder ABC 129E Sum Equals Xor
题目链接:https://atcoder.jp/contests/abc129/tasks/abc129_e 题目大意 给定一个二进制表示的数 L,问有多少对自然数 (a, b) 满足 $a + b ...
- day 65 Django基础一之web框架的本质
Django基础一之web框架的本质 django第一天 本节目录 一 web框架的本质及自定义web框架 二 模板渲染JinJa2 三 MVC和MTV框架 四 Django的下载安装 五 基 ...
- 3列滚动抽奖 jquery.slotmachine
效果图: 需引入js文件: <script src="js/jquery-3.2.0.js"></script> <script src=" ...
- mybatis中处理结果集映射
单行结果集映射: 接口中方法返回值定义为Map类型,sql语句的resultType属性设置为map即可.这种情况默认把列名作为key,列中的值作为value. 也就是说用map<Strirng ...
- 【珍惜时间】vuepro
老规矩放上大大的github开源地址:https://github.com/goodheart222/vuepro 我们再来看看项目的效果,初步根据效果做到心中有数 看到效果的话,我们会发现,肯定是有 ...
- git sync tags with remote
git 同步遠程標籤 在 .git/config的 [remote "origin"] 下加了 fetch = +refs/tags/*:refs/tags/* 最後就變成 [re ...
- openSUSE 安装compass,mkmf.rb can't find,checking for ffi.h...extconf.rb failed
安装compass时,提示 Fetching: sass-.gem (%) Successfully installed sass- Fetching: ffi-.gem (%) Building n ...
- css3 ---1 基本的选择器
基本的选择器 <style type="text/css"> /*通配符选择器*/ * { margin: ; padding: ; border: none; } / ...
- table方法也属于模型类的连贯操作方法之一
table方法也属于模型类的连贯操作方法之一,主要用于指定操作的数据表. 用法 一般情况下,操作模型的时候系统能够自动识别当前对应的数据表,所以,使用table方法的情况通常是为了: 切换操作的数据表 ...
