C# 递归与非递归算法与数学公式

1、递归

递归：程序调用自身的编程技巧称为递归（recursion）。

优点是：代码简洁，易于理解。

缺点是：运行效率较低。

递归思想：把问题分解成规模更小，但和原问题有着相同解法的问题。

1）下面是关于1+2+3+....+n的递归算法：

/// <summary>
/// 1+2+3+....+n的递归算法
/// </summary>
/// <param name="i"></param>
/// <returns></returns>
public static int Process1(int i)
{
    //计算1+2+3+4+...+100的值
    if (i == ) return ;
    return Process1(i - ) + i;
}

当i=3的时候，我觉得运算过程可能是这样的（个人理解）：

Process2(3- 1) + 3 =

Process2(2 - 1) + 2 + 3 =

Process2(1 - 1) + 1 + 2 + 3 =

最后结果：0 + 1 + 2 + 3 = 6

2）假设有50瓶饮料，喝完3个空瓶可以换一瓶，以此类推，请问总共喝了多少瓶饮料？

public static int Process1(int i,int num)
{
    if (i / num == ) return ;
    return Process1(i / num + i % num, num) + i;
}

其中 i=50，num=3。结果为：74瓶。

2、非递归

下面是用循环形式非递归代替上面的递归算法：

/// <summary>
/// 1+2+3+....+n的非递归算法
/// </summary>
/// <param name="isum"></param>
/// <returns></returns>
public static int Process2(int isum)
{
    int sum = ;
 
    for (int i = ; i <= isum; i++)
    {
        sum += i;
    }
    return sum;
}

3、公式

后来与同学讨论，发现了更简便的。

public static int Process3(int i)
{
    //计算1+2+3+4+...+100的值
    return i * (i + ) / ;
}

数学果然很厉害，用了一个公式，既简便又效率。

4、其他递归例子

(1) 斐波那契数列

/// <summary>
/// 斐波那契数列递归算法，用于计算第i位的值
/// </summary>
/// <param name="i"></param>
/// <returns></returns>
public static int Process(int i)
{
　　 //计算1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233.....第i列的值
    if (i == ) return ;
    if (i == ) return ;
    return Process(i - ) + Process(i - );
}

(2)n的阶乘

/// <summary>
/// 1*2*3*....*n的递归算法
/// </summary>
/// <param name="i"></param>
/// <returns></returns>
public static int Process(int i)
{
    //计算1*2*3*...*n的值
    if (i == ) return ;
    return Process(i - ) * i;
}

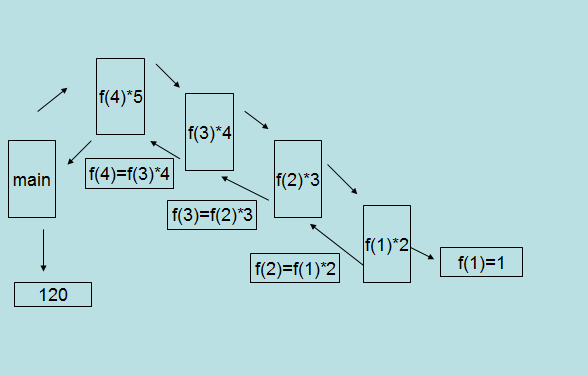
5、最后

下面分享个递归的实际例子（压缩时，查找某个文件夹里所有的文件）：C# 压缩文件 ICSharpCode.SharpZipLib.dll

---

相关文章：C# 冒泡排序