04. 寻找两个正序数组的中位数 Golang实现

题目：

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]

输出：2.00000

解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]

输出：2.50000

解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

思路分析:

我们通过二分查找一个较短的数组的某个切分点，计算出另一个数组对应的切分点，从而找到中位数。

问题分解：

输入：两个已排序的数组 nums1 和 nums2。

目标：找出这两个数组合并后有序数组的中位数。

要求：时间复杂度为 O(log(m + n))。

关键思路：

• [1 ] 中位数的定义：
  
  假设一个数组长度为m,
  
  对于奇数长度的合并数组，中位数是正中间的那个数,对应下标为m/2。
  
  对于偶数长度的合并数组，中位数是中间两个数的平均值,对应下标为(m-1)/2，m/2。
  
  下面为了统一不区分奇数偶数，可以使用：(m+1)/2,涉及到一个很关键的点，就是计算机的整除只取整数部分，即整体有几个偶数。如果原本是偶数，那么计算后的下标(m+1)/2,指向第二个数。而保证了第一个数：无论奇数偶数长度，都在这个下标的左侧。从而达到了统一公式的目的。那么合并两个数组，不确定哪个数组是奇数偶数，只需要记录下来分类点，从而可以获取到左右两侧的值。

• [2 ] 不直接合并数组：

  如果简单地合并数组再取中位数，时间复杂度是 O(m + n)，不符合题目要求。
  
  我们可以通过二分查找，将问题转换为寻找“两个数组的切分点”，使得切分线左边的数都小于右边的数。

• [ 3] 二分查找的核心思想：

  先选定较短的数组 nums1，假设长度为 m，较长的数组 nums2 长度为 n。
  
  我们在较短的数组 nums1 上进行二分搜索，找到一个合适的切分点 i。
  
  根据 i，可以计算出 nums2 的切分点 j = (m + n + 1) / 2 - i，这样保证总是有 (m + n + 1) / 2 个元素在左边。因为中位数在有序列表中的位置必然是合并后的数组的中间位置！

• [ 4] 找到中位数的条件：

  目标是找到两个切分点 i 和 j，使得：

  nums1[i-1] ≤ nums2[j]
  nums2[j-1] ≤ nums1[i]

也就是说，左边的最大值小于等于右边的最小值。如果这两个条件成立，那么说明切分点是合理的，可以得到最终中位数。

调整切分点：

如果 nums1[i-1] > nums2[j]，说明 i 太大了，需要左移。

如果 nums2[j-1] > nums1[i]，说明 i 太小了，需要右移。

通过不断调整 i，最终可以找到一个满足条件的切分点。

中位数的计算：

如果 m + n 是奇数，那么中位数就是左边部分的最大值，即 max(nums1[i-1], nums2[j-1])。

如果 m + n 是偶数，那么中位数是左边最大值和右边最小值的平均值，即 (max(nums1[i-1], nums2[j-1]) + min(nums1[i], nums2[j])) / 2。

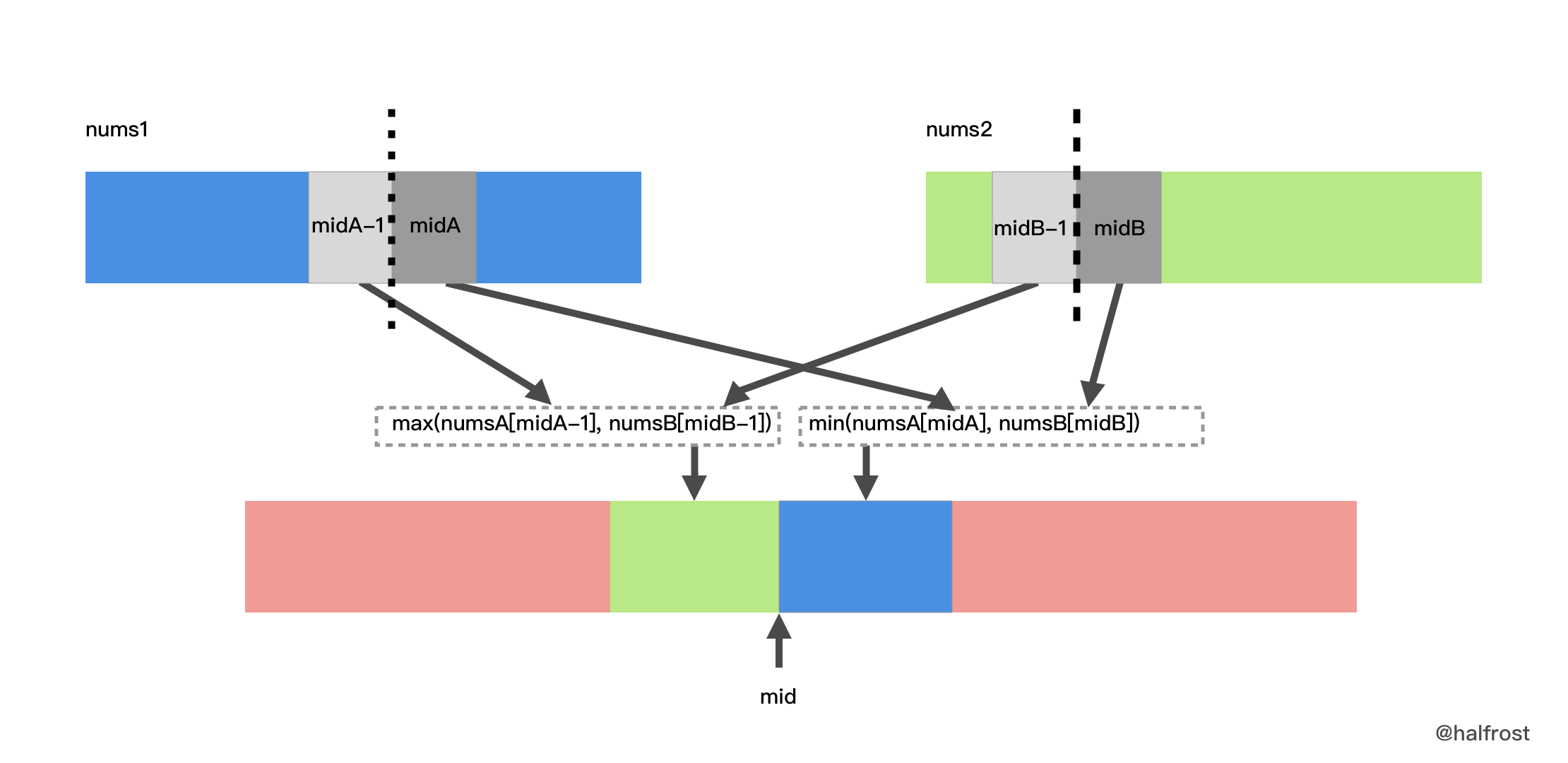
具体步骤：

• [ 1] 初始化：
  
  让 nums1 的长度为 m，nums2 的长度为 n。
  
  保证 nums1 的长度小于等于 nums2，即 m ≤ n。

• [2 ] 二分查找：
  
  在 nums1 上进行二分搜索。设定 i 为 nums1 的切分点，j 为 nums2 的切分点，满足 j = (m + n + 1) / 2 - i。通过二分调整 i 的位置，直到满足 nums1[i-1] ≤ nums2[j] 且 nums2[j-1] ≤ nums1[i]。
  
  找到切分点：

  如果找到满足条件的切分点，计算中位数：
  
  如果 m + n 是奇数，中位数就是左半部分的最大值。
  
  如果 m + n 是偶数，中位数是左半部分的最大值与右半部分的最小值的平均值。

• [3 ] 边界情况：
  
  当 i 或 j 为 0 或 m 时，需要特别处理，因为此时可能没有左边或右边的元素。
  
  边界处理情况详细说明：

1. nums1Mid == 0 和 nums1Mid == m 的情况：

• nums1Mid == 0 表示 nums1 的左边部分为空，没有左侧元素，此时划分线完全位于 nums1 的最左边。所以左边的最大值（midLeft）只能来自 nums2。
• nums1Mid == m 表示 nums1 的右边部分为空，划分线完全位于 nums1 的最右边。所以右边的最小值（midRight）只能来自 nums2。

1. nums2Mid == 0 和 nums2Mid == n 的情况：

• nums2Mid == 0 表示 nums2 的左边部分为空，此时 nums2 左侧没有元素，左边的最大值只能从 nums1 中取得。
• nums2Mid == n 表示 nums2 的右边部分为空，右边的最小值只能从 nums1 中取得。

点击查看代码

func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
    if len(nums1) > len(nums2) {
        return findMedianSortedArrays(nums2, nums1)
    }

    m, n := len(nums1), len(nums2)
    low, high, k := 0, m, (m+n+1)/2
    var nums1Mid, nums2Mid int

    for low <= high {
        nums1Mid = low + (high - low) / 2
        nums2Mid = k - nums1Mid

        if nums1Mid > 0 && nums1[nums1Mid-1] > nums2[nums2Mid] {
            // nums1Mid is too large, need to decrease
            high = nums1Mid - 1
        } else if nums1Mid < m && nums1[nums1Mid] < nums2[nums2Mid-1] {
            // nums1Mid is too small, need to increase
            low = nums1Mid + 1
        } else {
            // Found the correct partition
            break
        }
    }

    // Determine left half's maximum
    var midLeft int
    if nums1Mid == 0 {
        midLeft = nums2[nums2Mid-1]
    } else if nums2Mid == 0 {
        midLeft = nums1[nums1Mid-1]
    } else {
        midLeft = max(nums1[nums1Mid-1], nums2[nums2Mid-1])
    }

    // If total length is odd, return the left side's maximum
    if (m+n) % 2 == 1 {
        return float64(midLeft)
    }

    // Determine right half's minimum
    var midRight int
    if nums1Mid == m {
        midRight = nums2[nums2Mid]
    } else if nums2Mid == n {
        midRight = nums1[nums1Mid]
    } else {
        midRight = min(nums1[nums1Mid], nums2[nums2Mid])
    }

    // Return the average of the two middle values
    return float64(midLeft + midRight) / 2.0
}