poj 1265 Area 面积+多边形内点数

Area

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 5861		Accepted: 2612

Description

Being well known for its highly innovative products, Merck would definitely be a good target for industrial espionage. To protect its brand-new research and development facility the company has installed the latest system of surveillance robots patrolling the area. These robots move along the walls of the facility and report suspicious observations to the central security office. The only flaw in the system a competitor抯 agent could find is the fact that the robots radio their movements unencrypted. Not being able to find out more, the agent wants to use that information to calculate the exact size of the area occupied by the new facility. It is public knowledge that all the corners of the building are situated on a rectangular grid and that only straight walls are used. Figure 1 shows the course of a robot around an example area.

 
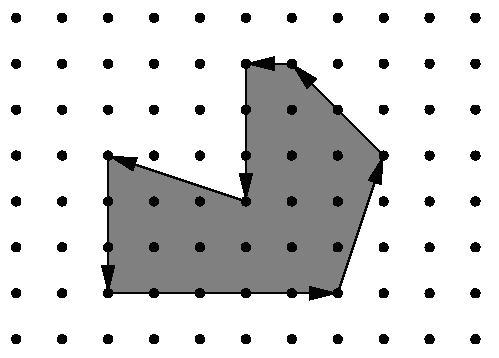
Figure 1: Example area. 
You are hired to write a program that calculates the area occupied by the new facility from the movements of a robot along its walls. You can assume that this area is a polygon with corners on a rectangular grid. However, your boss insists that you use a formula he is so proud to have found somewhere. The formula relates the number I of grid points inside the polygon, the number E of grid points on the edges, and the total area A of the polygon. Unfortunately, you have lost the sheet on which he had written down that simple formula for you, so your first task is to find the formula yourself. 

Input

The first line contains the number of scenarios. 
For each scenario, you are given the number m, 3 <= m < 100, of movements of the robot in the first line. The following m lines contain pairs 揹x dy�of integers, separated by a single blank, satisfying .-100 <= dx, dy <= 100 and (dx, dy) != (0, 0). Such a pair means that the robot moves on to a grid point dx units to the right and dy units upwards on the grid (with respect to the current position). You can assume that the curve along which the robot moves is closed and that it does not intersect or even touch itself except for the start and end points. The robot moves anti-clockwise around the building, so the area to be calculated lies to the left of the curve. It is known in advance that the whole polygon would fit into a square on the grid with a side length of 100 units. 

Output

The output for every scenario begins with a line containing 揝cenario #i:� where i is the number of the scenario starting at 1. Then print a single line containing I, E, and A, the area A rounded to one digit after the decimal point. Separate the three numbers by two single blanks. Terminate the output for the scenario with a blank line.

Sample Input

2
4
1 0
0 1
-1 0
0 -1
7
5 0
1 3
-2 2
-1 0
0 -3
-3 1
0 -3

Sample Output

Scenario #1:
0 4 1.0

Scenario #2:
12 16 19.0

/*
poj 1265 Area 面积+多边形内点数

给你初始点以及每次走的方向,可以得到n个点的集合.然后计算这个多边的面积,多边形
内部包含的点数以及多边形边上的点数

因为多边形顶点都是整点,所以通过皮克定理可以得出其面积S和内部格点数目i、
边上格点数目j的关系：S = i + j/2 - 1.
所以我们可以先计算出多边的面积. 多边形边上的点数j满足一个GCD关系,可以求出
于是便能得到i

hhh-2016-05-08 20:01:56
*/
#include <iostream>
#include <vector>
#include <cstring>
#include <string>
#include <cstdio>
#include <queue>
#include <cmath>
#include <algorithm>
#include <functional>
#include <map>
using namespace std;
#define lson  (i<<1)
#define rson  ((i<<1)|1)
typedef long long ll;
using namespace std;
const int  maxn = 10100;
double PI = 3.1415926;
double eps = 1e-8;

int sgn(double x)
{
    if(fabs(x) < eps) return 0;
    if(x < 0)
        return -1;
    else
        return 1;
}

struct Point
{
    double x,y;
    Point() {}
    Point(double _x,double _y)
    {
        x = _x,y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x-b.x,y-b.y);
    }
    double operator ^(const Point &b)const
    {
        return x*b.y-y*b.x;
    }
    double operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
};

struct Line
{
    Point s,t;
    Line() {}
    Line(Point _s,Point _t)
    {
        s = _s;
        t = _t;
    }
    pair<int,Point> operator &(const Line&b)const
    {
        Point res = s;
        if( sgn((s-t) ^ (b.s-b.t)) == 0)   //通过叉积判断
        {
            if( sgn((s-b.t) ^ (b.s-b.t)) == 0)
                return make_pair(0,res);
            else
                return make_pair(1,res);
        }
        double ta = ((s-b.s)^(b.s-b.t))/((s-t)^(b.s-b.t));
        res.x += (t.x-s.x)*ta;
        res.y += (t.y-s.y)*ta;
        return make_pair(2,res);
    }
};
Point lis[maxn];
int Stack[maxn],top;

double dist(Point a,Point b)
{
    return sqrt((a-b)*(a-b));
}
bool cmp(Point a,Point b)
{
    double t = (a-lis[0])^(b-lis[0]);
    if(sgn(t) == 0)
    {
        return dist(a,lis[0]) <= dist(b,lis[0]);
    }
    if(sgn(t) < 0)
        return false;
    else
        return true;
}

bool Cross(Point a,Point b,Point c)
{
   return  (b.y-a.y)*(c.x-b.x) == (c.y-b.y)*(b.x-a.x);
}

int GCD(int a,int b)
{
    if(a < b)swap(a,b);
    if(b == 0)
        return a;
    while(a % b)
    {
        int t = a%b;
        a = b;
        b = t;
    }
    return b;
}

int main()
{
   // freopen("in.txt","r",stdin);
    int n,T;
    int cas = 1;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        double x=0,y=0;
        double x1,y1;
        for(int i = 0; i < n; i++)
        {
            scanf("%lf%lf",&x1,&y1);
            lis[i].x = x+x1;
            lis[i].y = y+y1;
            x = lis[i].x;
            y = lis[i].y;
        }
        printf("Scenario #%d:\n",cas++);
        double res = 0;
        for(int i = 0;i < n;i++)
        {
            res += (lis[i]^lis[(i+1)%n])/2;
        }
        int Onum = 0;
        for(int i = 0;i < n;i++)
        {
            int tx = abs(lis[i].x - lis[(i+1)%n].x);
            int ty = abs(lis[i].y - lis[(i+1)%n].y);
            Onum += GCD(tx,ty);
        }
        int Inum = res*2+2-Onum;
        printf("%d %d %.1f\n\n",Inum/2,Onum,res);
    }
    return 0;
}