poj 1265&&poj 2954(Pick定理)

Area

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 5811		Accepted: 2589

Description

Being well known for its highly innovative products, Merck would definitely be a good target for industrial espionage. To protect its brand-new research and development facility the company has installed the latest system of surveillance robots patrolling the area. These robots move along the walls of the facility and report suspicious observations to the central security office. The only flaw in the system a competitor抯 agent could find is the fact that the robots radio their movements unencrypted. Not being able to find out more, the agent wants to use that information to calculate the exact size of the area occupied by the new facility. It is public knowledge that all the corners of the building are situated on a rectangular grid and that only straight walls are used. Figure 1 shows the course of a robot around an example area.

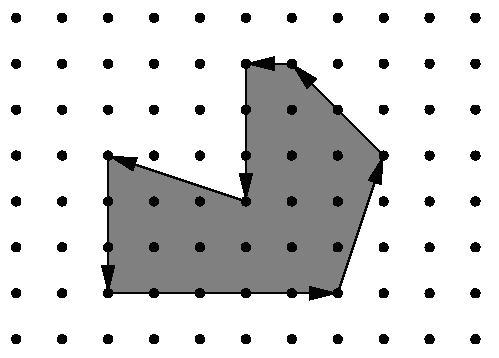
Figure 1: Example area.

You are hired to write a program that calculates the area occupied
by the new facility from the movements of a robot along its walls. You
can assume that this area is a polygon with corners on a rectangular
grid. However, your boss insists that you use a formula he is so proud
to have found somewhere. The formula relates the number I of grid points
inside the polygon, the number E of grid points on the edges, and the
total area A of the polygon. Unfortunately, you have lost the sheet on
which he had written down that simple formula for you, so your first
task is to find the formula yourself.

Input

The first line contains the number of scenarios.

For each scenario, you are given the number m, 3 <= m < 100,
of movements of the robot in the first line. The following m lines
contain pairs 揹x dy�of integers, separated by a single blank, satisfying
.-100 <= dx, dy <= 100 and (dx, dy) != (0, 0). Such a pair means
that the robot moves on to a grid point dx units to the right and dy
units upwards on the grid (with respect to the current position). You
can assume that the curve along which the robot moves is closed and that
it does not intersect or even touch itself except for the start and end
points. The robot moves anti-clockwise around the building, so the area
to be calculated lies to the left of the curve. It is known in advance
that the whole polygon would fit into a square on the grid with a side
length of 100 units.

Output

The
output for every scenario begins with a line containing 揝cenario #i:�
where i is the number of the scenario starting at 1. Then print a single
line containing I, E, and A, the area A rounded to one digit after the
decimal point. Separate the three numbers by two single blanks.
Terminate the output for the scenario with a blank line.

Sample Input

2
4
1 0
0 1
-1 0
0 -1
7
5 0
1 3
-2 2
-1 0
0 -3
-3 1
0 -3

Sample Output

Scenario #1:
0 4 1.0

Scenario #2:
12 16 19.0

题意:一个多边形从某个点出发(假设从0,0出发),每次有一个增量(dx,dy)!=(0,0) 经过n次之后又回到了原点
组成了一个简单多边形.问此时多边形内部的整点的数量,多边形边上的整点的数量,多边形的面积.

Pick定理：一个计算点阵中顶点在格点上的多边形面积公式：S=a+b/2-1，其中a表示多边形内部的整点数，b表示
多边形边界上的整点数，s表示多边形的面积。(ps:整点是x,y坐标都是整数)
每条边上的格点数(顶点只算终点) = gcd(abs(x2-x1),abs(y2-y1))

///题意:一个多边形从某个点出发(假设从0,0出发),每次有一个增量(dx,dy)!=(0,0) 经过n次之后又回到了原点
///组成了一个简单多边形.问此时多边形内部的整点的数量,多边形边上的整点的数量,多边形的面积.
///Pick定理：一个计算点阵中顶点在格点上的多边形面积公式：S=a+b/2-1，其中a表示多边形内部的整点数，b表示
///多边形边界上的整点数，s表示多边形的面积。(ps:整点是x,y坐标都是整数)
///每条边上的格点数 = gcd(abs(x2-x1),abs(y2-y1))
#include <iostream>
#include <cstdio>
#include <cstring>
#include <math.h>
#include <algorithm>
#include <stdlib.h>
using namespace std;
const int N =;
struct Point {
    int x,y;
}p[N];
int gcd(int a,int b){
    return b==?a:gcd(b,a%b);
}
int cross(Point a,Point b,Point c){
    return (a.x-c.x)*(b.y-c.y)-(a.y-c.y)*(b.x-c.x);
}
int main()
{
    int tcase;
    scanf("%d",&tcase);
    int k = ;
    while(tcase--){
        int n;
        scanf("%d",&n);
        p[].x = ,p[].y = ;
        int On=,In=;
        double area=;
        for(int i=;i<=n;i++){
            int dx,dy;
            scanf("%d%d",&dx,&dy);
            p[i].x= p[i-].x+dx;
            p[i].y=p[i-].y+dy;
            On+=gcd(abs(dx),abs(dy));
        }
        for(int i=;i<n-;i++){
            area+=cross(p[i],p[i+],p[])/2.0;
        }
        In = (int)(area+-On/);
        printf("Scenario #%d:\n%d %d %.1lf\n\n",k++,In,On,area);
    }
    return ;
}

poj 2954

http://acm.pku.edu.cn/JudgeOnline/problem?id=2954

///题意:完全包含在三角形内的整点有多少
#include <iostream>
#include <cstdio>
#include <cstring>
#include <math.h>
#include <algorithm>
#include <stdlib.h>
using namespace std;
struct Point {
    int x,y;
}p1,p2,p3;
int gcd(int a,int b){
    return b==?a:gcd(b,a%b);
}
int cross(Point a,Point b,Point c){
    return (a.x-c.x)*(b.y-c.y)-(a.y-c.y)*(b.x-c.x);
}
int main()
{
    while(scanf("%d%d%d%d%d%d",&p1.x,&p1.y,&p2.x,&p2.y,&p3.x,&p3.y)!=EOF){
        if(p1.x==&&p1.y==&&p2.x==&&p2.y==&&p3.x==&&p3.y==) break;
        double area = fabs(cross(p2,p3,p1)/2.0);

        int On = gcd(abs(p2.x-p1.x),abs(p2.y-p1.y))+gcd(abs(p3.x-p2.x),abs(p3.y-p2.y))+gcd(abs(p3.x-p1.x),abs(p3.y-p1.y));
        printf("%d\n",(int)(area+-On/));
    }
    return ;
}