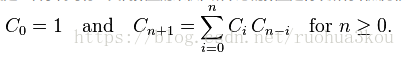[leetcode] 96 Unique Binary Search Trees (Medium)
字母题
思路:
一开始妹有一点思路,去查了二叉查找树,发现有个叫做卡特兰数的东西。
1、求可行的二叉查找树的数量,只要满足中序遍历有序。
2、以一个结点为根的可行二叉树数量就是左右子树可行二叉树数量的乘积。
3、总的数量是将以所有结点为根的可行结果累加起来。
n = 0 时,因为空树也算一种二叉搜索树,则dp[0]=1;
n = 1时,dp[1]=1;
n = 2时
dp[2] = dp[0] * dp[1] (1为根的情况)
+ dp[1] * dp[0] (2为根的情况)
n = 3时
dp[3] = dp[0] * dp[2] (1为根的情况)
+ dp[1] * dp[1] (2为根的情况)
+ dp[2] * dp[0] (3为根的情况)
写成表达式如下:
class Solution
{
public:
int numTrees(int n)
{
if (n <= 0)
return 0;
int res[n + 1] = {0};
res[0] = 1;
res[1] = 1;
for (int i = 2; i <= n; i++)
{
for (int j = 0; j < i; j++)
{
res[i] += res[i - j - 1] * res[j];
}
}
return res[n];
}
};
[leetcode] 96 Unique Binary Search Trees (Medium)的更多相关文章
- [LeetCode] 96. Unique Binary Search Trees 唯一二叉搜索树
Given n, how many structurally unique BST's (binary search trees) that store values 1...n? For examp ...
- 52. leetcode 96. Unique Binary Search Trees
96. Unique Binary Search Trees Given n, how many structurally unique BST's (binary search trees) tha ...
- leetcode 96. Unique Binary Search Trees 、95. Unique Binary Search Trees II 、241. Different Ways to Add Parentheses
96. Unique Binary Search Trees https://www.cnblogs.com/grandyang/p/4299608.html 3由dp[1]*dp[1].dp[0]* ...
- [LeetCode] 96. Unique Binary Search Trees(给定一个数字n,有多少个唯一二叉搜索树) ☆☆☆
[Leetcode] Unique binary search trees 唯一二叉搜索树 Unique Binary Search Trees leetcode java 描述 Given n, h ...
- [LeetCode] 96. Unique Binary Search Trees 独一无二的二叉搜索树
Given n, how many structurally unique BST's (binary search trees) that store values 1 ... n? Example ...
- leetcode 96 Unique Binary Search Trees ----- java
Given n, how many structurally unique BST's (binary search trees) that store values 1...n? For examp ...
- Java [Leetcode 96]Unique Binary Search Trees
题目描述: Given n, how many structurally unique BST's (binary search trees) that store values 1...n? For ...
- [leetcode]96. Unique Binary Search Trees给定节点形成不同BST的个数
Given n, how many structurally unique BST's (binary search trees) that store values 1 ... n? Input: ...
- [leetcode]95. Unique Binary Search Trees II给定节点形成不同BST的集合
Given an integer n, generate all structurally unique BST's (binary search trees) that store values 1 ...
随机推荐
- 转载 《我用 TypeScript 语言的七个月》
快速使用Romanysoft LAB的技术实现 HTML 开发Mac OS App,并销售到苹果应用商店中. <HTML开发Mac OS App 视频教程> 土豆网同步更新:http: ...
- 记住以下10条,Linux磁盘与文件系统管理无忧矣
1.查看当前Linux系统所支持的文件系统:ls -l /lib/modules/$(uname -r)/kernel/fs:目前已加载到内存中支持的文件系统:cat /proc/filesystem ...
- 使窗体拥有透明效果的API
一.背景FlashGet的透明效果大家羡慕吧.传统的Windows应用程序想实现半透明效果,一般来说需要处理自己的窗口的WM_Paint消息窗口,很麻烦.现在好了,SetLayeredWindowAt ...
- 因为 'PRIMARY' 文件组已满。请删除不需要的文件、删除文件组中的对象、将其他文件添加到文件组或为文件组中的现有文件启用自动增长,以便增加可用磁盘空间
导致你的问题的,应该有2种可能性: 1.存放你的primary文件组的磁盘,已经满了: use master--你的数据库名称 go --看看你的primary组里的文件 select ds.name ...
- MySQL之SQL优化详解(二)
目录 MySQL之SQL优化详解(二) 1. SQL的执行顺序 1.1 手写顺序 1.2 机读顺序 2. 七种join 3. 索引 3.1 索引初探 3.2 索引分类 3.3 建与不建 4. 性能分析 ...
- spring 5.x 系列第20篇 ——spring简单邮件、附件邮件、内嵌资源邮件、模板邮件发送 (代码配置方式)
源码Gitub地址:https://github.com/heibaiying/spring-samples-for-all 一.说明 1.1 项目结构说明 邮件发送配置类为com.heibaiyin ...
- 【STL】集合运算
STL中有可以实现交集.并集.差集.对称差集的算法. 使用前需要包含头文件: #include <algorithm> 注:使用计算交集和并集的算法必须保证参与运算的两个集合有序!!! 交 ...
- zphp源码分析(一)
zphp是一款轻量级的php服务端框架,是swoole官方开发的.可以用来开发web应用和网络服务. 安装: 可以通过composer安装, { "require": { &quo ...
- (一)C#编程基础复习——开启编程之旅
回想当年学习编程,刚开始学习是非常艰苦的,可能是因为文科生原因,刚开始接触工科类的知识不是很擅长,上去大学第一年基本没有好好学习编程,入门C#编程基础一窍不通,也许那时年少无知,第二学期开始奋发图强, ...
- 跟着大彬读源码 - Redis 1 - 启动服务,程序都干了什么?
一直很羡慕那些能读 Redis 源码的童鞋,也一直想自己解读一遍,但迫于 C 大魔王的压力,解读日期遥遥无期. 相信很多小伙伴应该也都对或曾对源码感兴趣,但一来觉得自己不会 C 语言,二来也不知从何入 ...