二分图匹配——p3386 p2071 p2319 p1129（矩阵游戏）

---恢复内容开始---

二分图，就是给你一个图，可以将点分为两部分，每一部分的点都能唯一映射到另一个集合里，也就是有连边；

注：以下转自 http://blog.csdn.net/dark_scope/article/details/8880547

匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

-------等等，看得头大？那么请看下面的版本：

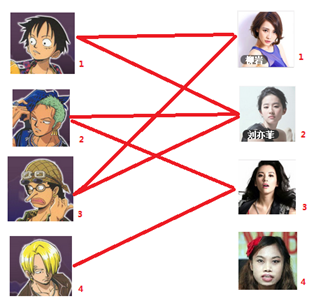
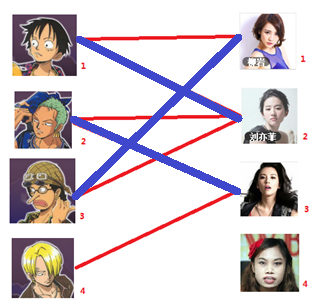
通过数代人的努力，你终于赶上了剩男剩女的大潮，假设你是一位光荣的新世纪媒人，在你的手上有N个剩男，M个剩女，每个人都可能对多名异性有好感（-_-||暂时不考虑特殊的性取向），如果一对男女互有好感，那么你就可以把这一对撮合在一起，现在让我们无视掉所有的单相思（好忧伤的感觉），你拥有的大概就是下面这样一张关系图，每一条连线都表示互有好感。

本着救人一命，胜造七级浮屠的原则，你想要尽可能地撮合更多的情侣，匈牙利算法的工作模式会教你这样做：

===============================================================================

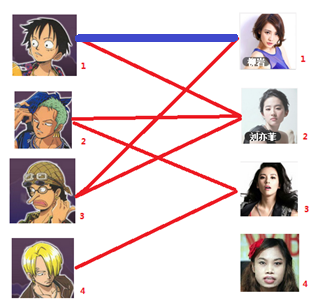
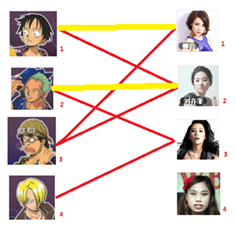
一： 先试着给1号男生找妹子，发现第一个和他相连的1号女生还名花无主，got it，连上一条蓝线

===============================================================================

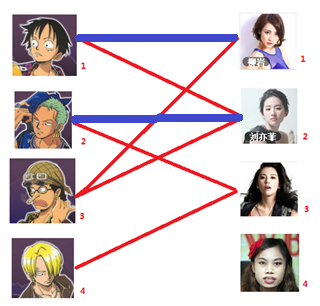
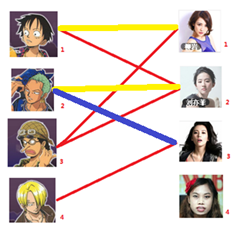
二：接着给2号男生找妹子，发现第一个和他相连的2号女生名花无主，got it

===============================================================================

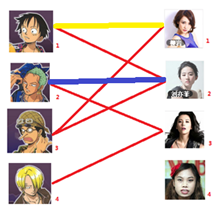
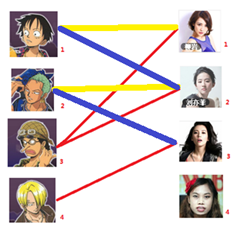
三：接下来是3号男生，很遗憾1号女生已经有主了，怎么办呢？

我们试着给之前1号女生匹配的男生（也就是1号男生）另外分配一个妹子。

(黄色表示这条边被临时拆掉)

与1号男生相连的第二个女生是2号女生，但是2号女生也有主了，怎么办呢？我们再试着给2号女生的原配()重新找个妹子(注意这个步骤和上面是一样的，这是一个递归的过程)

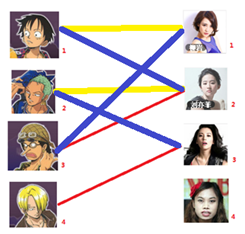
此时发现2号男生还能找到3号女生，那么之前的问题迎刃而解了，回溯回去

2号男生可以找3号妹子~~~                  1号男生可以找2号妹子了~~~                3号男生可以找1号妹子

所以第三步最后的结果就是：

===============================================================================

四： 接下来是4号男生，很遗憾，按照第三步的节奏我们没法给4号男生腾出来一个妹子，我们实在是无能为力了……香吉士同学走好。

===============================================================================

这就是匈牙利算法的流程，其中找妹子是个递归的过程，最最关键的字就是“腾”字

其原则大概是：有机会上，没机会创造机会也要上

这个讲的挺好的；

这个是模板，但是邻接矩阵应用限制大；

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=;
int n,m,e;
int edge[maxn][maxn];
int cp[maxn];
int ask[maxn];
int ans;

bool search(int x)
{
    for(int i=;i<=m;i++)
    {
        if(edge[x][i])
        {
            if(ask[i]) continue;
            ask[i]=;
            if(!cp[i]||search(cp[i]))
            {
                cp[i]=x;
                return ;
            }
        }
    }
    return ;
}
void matching()
{
    memset(cp,,sizeof(cp));
    for(int i=;i<=n;i++)
    {
        memset(ask,,sizeof(ask));
        if(search(i))
        {
            ans++;
        }
    }
}

int main()
{
    scanf("%d%d%d",&n,&m,&e);
    for(int i=;i<=e;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        if(x<=n&&y<=m)
        {
            edge[x][y]=;
            //vis[y][x]=1;
        }
    }
    matching();
    printf("%d",ans);
    return ;
}

P2071 座位安排

还是前式链向星舒服

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=;
int n,m;
int pre[maxn*],last[maxn],other[maxn*],l;

void add(int x,int y)
{
    l++;
    pre[l]=last[x];
    last[x]=l;
    other[l]=y;
}

int ans,cp[maxn][],ask[maxn][];
//int ask2[maxn],cp2[maxn];

bool search(int x)
{
    for(int p=last[x];p;p=pre[p])
    {
        int v=other[p];
        for(int i=;i<=;i++)
        {
            if(!ask[v][i])
            {
                ask[v][i]=;
                if(!cp[v][i]||search(cp[v][i]))
                {
                    cp[v][i]=x;
                    return ;
                }
            }
            /*if(!ask2[i])
            {
                ask2[i]=1;
                if(!cp2[i]||search(cp2[i]))
                {
                    cp2[i]=x;
                    return 1;
                }
            }*/
        }
    }
    return ;
}

void matching()
{
    memset(cp,,sizeof(cp));
    for(int i=;i<=*n;i++)
    {
        memset(ask,,sizeof(ask));
        //memset(ask2,0,sizeof(ask2));
        if(search(i))
        {
            ans++;
        }
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=;i<=*n;i++)
    {
        int x,s;
        scanf("%d",&s);
        scanf("%d",&x);
        add(i,x);
        add(i,s);
    }
    matching();
    printf("%d",ans);
    return ;
}

这个匈牙利算法我个人的理解就是先匹配，然后再递归替换；

P2319 [HNOI2006]超级英雄

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=;
int n,m;
int pre[maxn],last[maxn],other[maxn],l;
int cp[maxn],ask[maxn];
void add(int x,int y)
{
    l++;
    pre[l]=last[x];
    last[x]=l;
    other[l]=y;
}
int ans;
int num[maxn];
bool search(int x)
{
    for(int p=last[x];p;p=pre[p])
    {
        int v=other[p];
        if(ask[v]) continue;
        ask[v]=;
        if(!cp[v]||search(cp[v]))
        {
            cp[v]=x;
            num[x]=v;
            return ;
        }
    }
    return ;
}

void matching()
{
    memset(cp,,sizeof(cp));
    for(int i=;i<=n;i++)
    {
        memset(ask,,sizeof(ask));
        if(search(i))
        {
            ans++;
        }
        else break;
    }
}

int main()
{
    scanf("%d%d",&m,&n);
    for(int i=;i<=n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        if(x!=y)
        {
            add(i,x+);
            add(i,y+);
        }
        else add(i,x+);
    }
    matching();
    printf("%d\n",ans);
    for(int i=;i<=ans;i++)
    {
        printf("%d\n",num[i]-);
    }
    return ;
}

这几道题都是大同小异；

p1129矩阵游戏到是有点思维含量；

问是否可行，其实可以看出，就是行与列的匹配

如果g[i][j]==1，那么就给ij连一条边；

如果每行和每列都能成功匹配就是有解；

因为ij是1啊，如果这两个能匹配，这行和列都不能动，其他行只能找别的；

根据互换总能换成符合题意的形式；

（注意范围）

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=;
int t;
int n,g[maxn][maxn];
int pre[maxn*maxn],last[maxn*maxn],other[maxn*maxn],l;
void add(int x,int y)
{
    l++;
    pre[l]=last[x];
    last[x]=l;
    other[l]=y;
}
int cp[maxn],ask[maxn];
int ans;

bool search(int x)
{
    for(int p=last[x];p;p=pre[p])
    {
        int v=other[p];
        if(ask[v]) continue;
        ask[v]=;
        if(!cp[v]||search(cp[v]))
        {
            cp[v]=x;
            return ;
        }
    }
    return ;
}
void matching()
{
    memset(cp,,sizeof(cp));
    for(int i=;i<=n;i++)
    {
        memset(ask,,sizeof(ask));
        if(search(i))
        {
            ans++;
        }
    }
}
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        l=;ans=;
        memset(last,,sizeof(last));
        scanf("%d",&n);
        for(int i=;i<=n;i++)
        {
            for(int j=;j<=n;j++)
            {
                scanf("%d",&g[i][j]);
                if(g[i][j])
                {
                    add(i,j);
                }
            }
        }
        matching();
        if(ans==n) printf("Yes\n");
        else printf("No\n");
    }
    return ;
}