算法学习——st表

st表是一种基于倍增思想的DP。

用于求一个数列中的某个区间的最大/最小值。

用st[i][j]表示从第i个开始往后2^j个点，最大的是多少。

我们令k[i]表示2^i等于多少

那么有转移方程

st[i][j] = max(st[i][j - 1], st[i + k[i - 1]][j - 1]);

为什么呢？

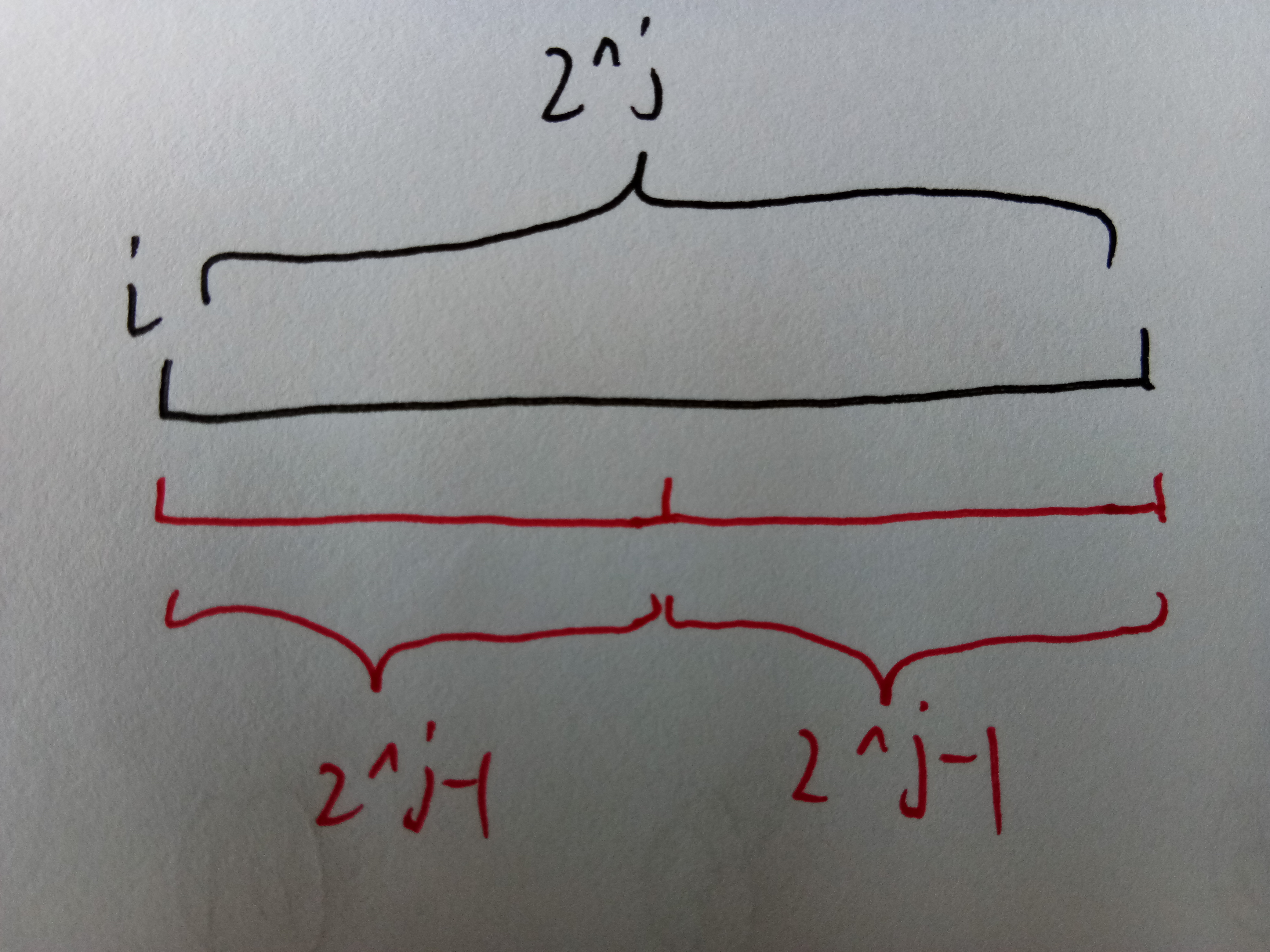
例如这幅图，显然黑色块的答案可以由合并下面两块得到。

那如果查询的时候不是2的整次幂怎么办？

这其实是没有问题的，你可以观察下图……

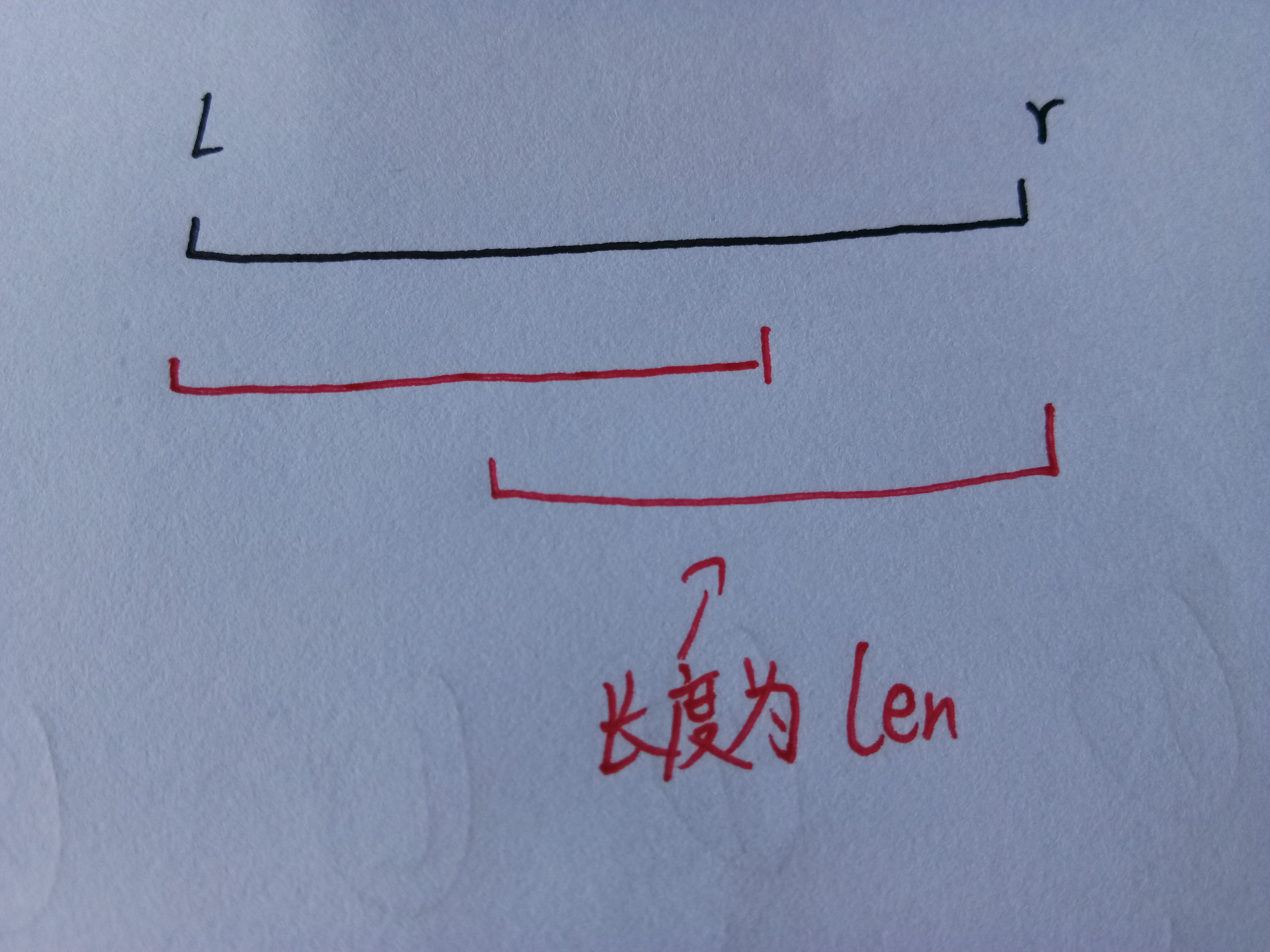
因为小区间有重叠部分并不影响，因此完全可以用稍大一点的小区间凑出大区间。
预处理一点信息以快速查询答案即可。

(早期代码，没有空格空行，略丑）

 #include<bits/stdc++.h>
 using namespace std;
 int n,m,s[],f[][],p[];
 int Max(int a,int b)
 {
     if(a>b)return a;
     else return b;
 }
 int Min(int a,int b)
 {
     if(a<b)return a;
     else return b;
 }
 void pre()
 {
     int i,a,key=;
     for(i=;i<=n;i++)
     {
         if(i==(key<<))p[i]=p[i-]+,key<<=;
         else p[i]=p[i-];
         scanf("%d",&a);
         f[i][]=a;
     }
     for(int j=;j<=;j++)
         for(i=;i<=n;i++)
         {
             f[i][j]=Max(f[i][j-],f[Min(i+(<<(j-)),n)][j-]);
         }
 }
 int main()
 {
     int i,a,b,k;
     scanf("%d%d",&n,&m);
     pre();
     for(i=;i<=m;i++)
     {
         scanf("%d%d",&a,&b);
         k=p[b-a+];
         printf("%d\n",Max(f[a][k],f[b-(<<k)+][k]));
     }
     return ;
 }