AOV图与拓扑排序&AOE图与关键路径

AOV网：所有的工程或者某种流程可以分为若干个小的工程或阶段，这些小的工程或阶段就称为活动。若以图中的顶点来表示活动，有向边表示活动之间的优先关系，则这样活动在顶点上的有向图称为AOV网。

拓扑排序算法：

（1）从AOV网中选择一个没有前驱的顶点（该顶点入度为0）并且输出它。

（2）从网中删去该顶点，并且删去从该顶点发出的全部有向边。

（3）重复上述两步，知道剩余的网中不再存在没有前驱的顶点为止。

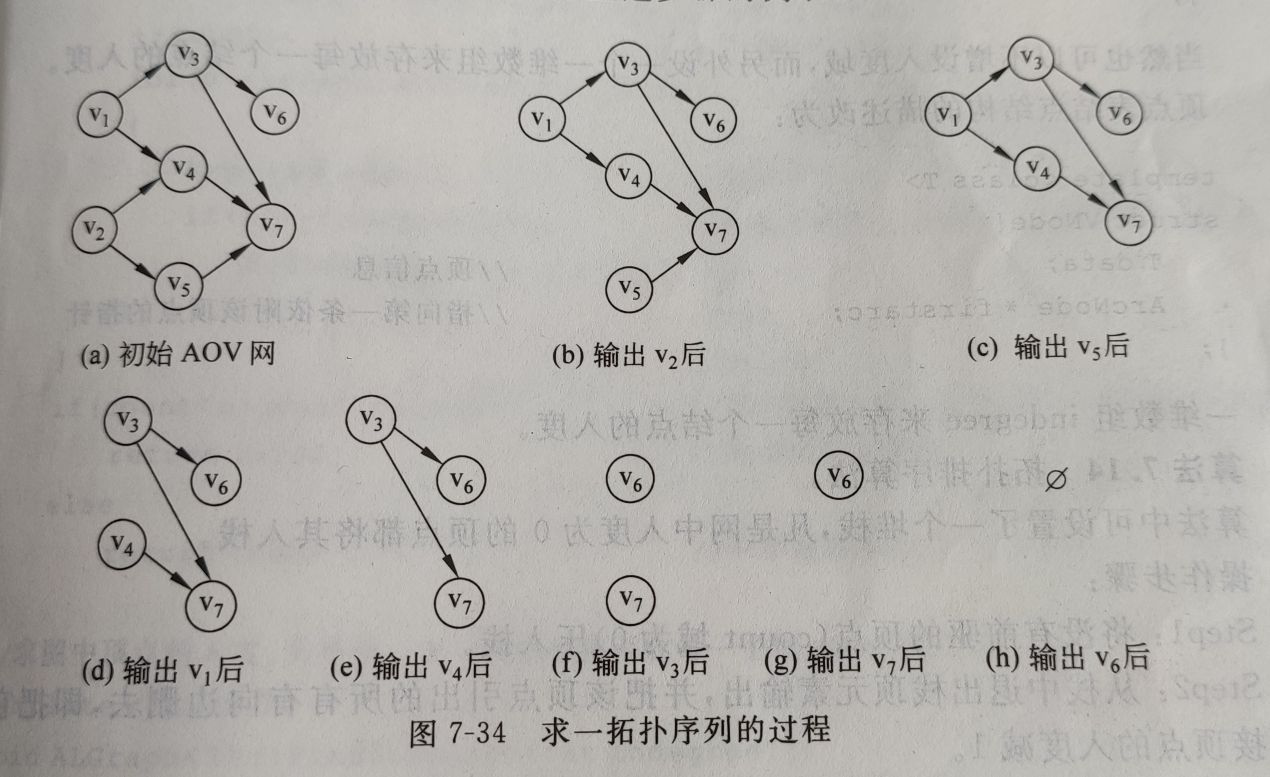
拓扑排序：v2,v5,v1,v4,v3,v7,v6

---

AOE图：若在带权的有向图中，以顶点表示事件，以有向边表示活动，边上的权值表示活动的开销（如该活动持续的事件），则此带权的有向图称为AOE网。

AOE网具有的性质：

（1)只有在某顶点代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始。

（2）只有在进入某一顶点的各有向边所代表的活动都已经结束，该顶点所代表的事件才能发生。

关键路径：

由于AOE网中的某些活动能够同时进行，故完成整个工程所必须花费的时间应该为源点到终点的最大路径长度（这里的路径长度指该路径上各个活动所需时间之和）。具有最大路径长度的路径称为关键路径。关键路径上的活动称为关键活动。关键路径长度是整个工程所需的最短工期。要缩短整个工期，必须加快关键活动的进度。

工程管理需要解决问题：*计算完成整个工期的最短路径  *确定关键路径，以找出哪些活动是影响工程进度的关键

---

---

关键路径的确认：

（1）事件的最早发生时间ve[k]

从源点到顶点的最大路径长度所代表的时间。理解：从前往后，前驱结点到当前结点所需时间，取最大值。

个人理解：只有进入某一顶点的所有有向边代表的活动都结束了，事件才能发生，所以取max，否则事件不发生。

（2）事件的最迟发生时间vl[k]

在不推迟整个工期的前提下事件v_k允许的最晚发生时间。 理解：从后往前，后继结点的最迟发生时间-边权值，取最小值。

（3）活动a_i的最早开始时间

活动a_i由弧<v_k,v_j>表示，只有事件v_k发生了，活动a_i才能开始。所以活动a_i最早开始事件=事件v_k最早发生时间。

（4）活动a_i的最晚开始时间l[i]

在不推迟整个工程完成日期的前提下必须开始的最晚时间

l[i]=vl[j]-dut(<v_k,v_j>)

最早完工时间——等于当前边指向结点的最早发生时间。

最晚完工时间——等于当前边指向结点的最迟发生时间。

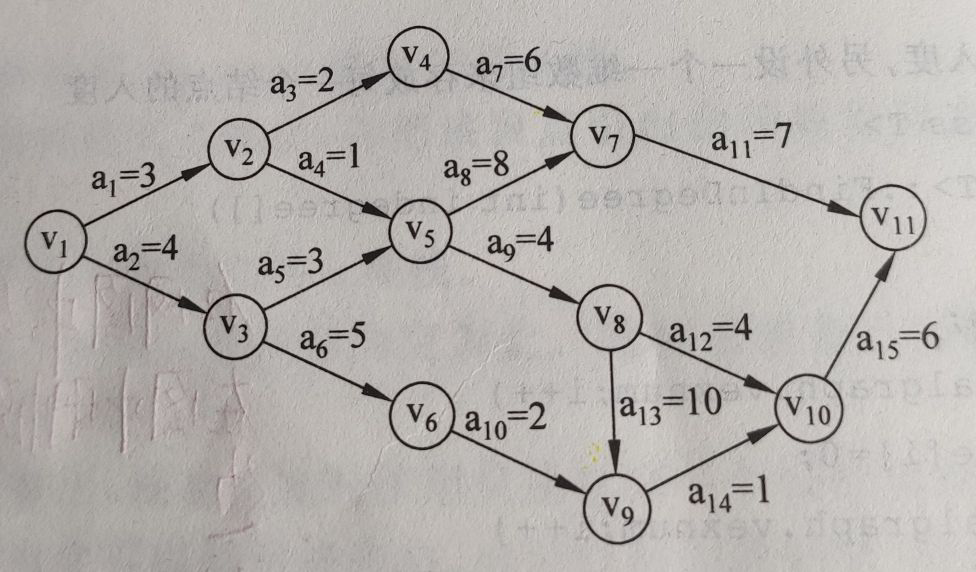
事件的最早发生时间

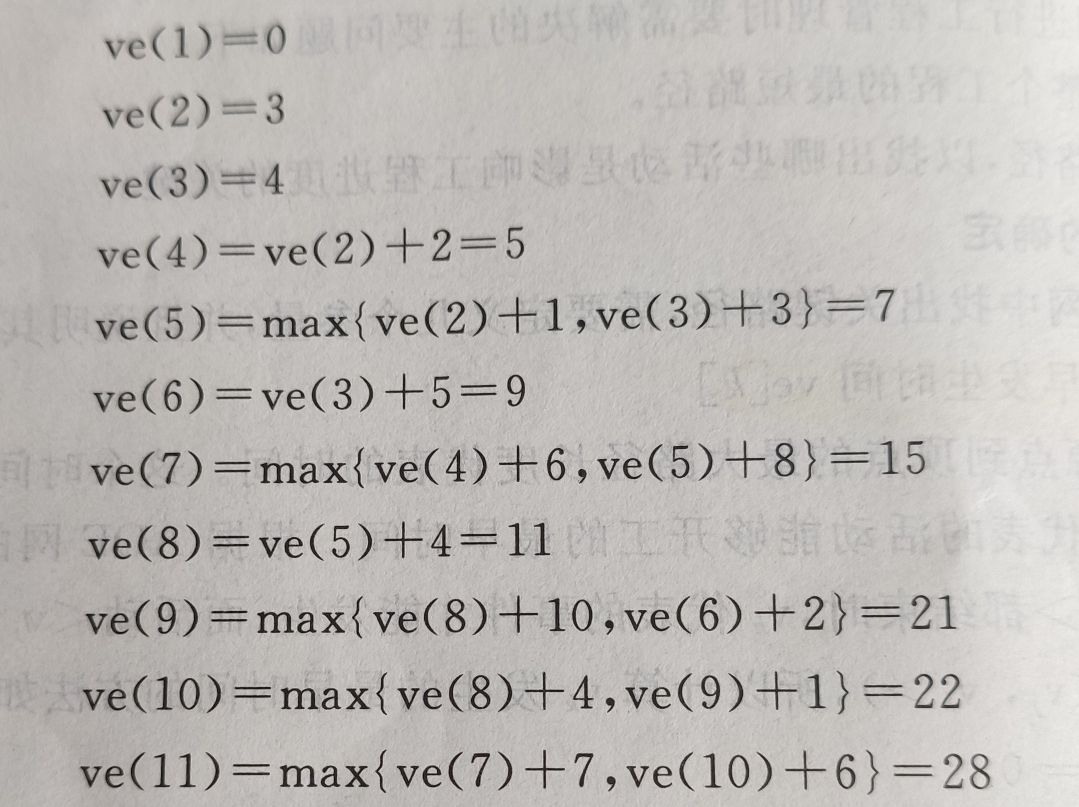
事件的最迟发生事件

活动ai的最早开始时间e[i]和最晚开始时间l[i]、

e[1]=ve[1]=0   e[2]=ve[1]=0    e3=ve[2]=3    e[4]=ve[2]=3   e[5]=ve[3]=4............

l[1]=vl[2]-3=3  l[2]=vl[3]-4=0   l[3]=vl[4]-2=13.......

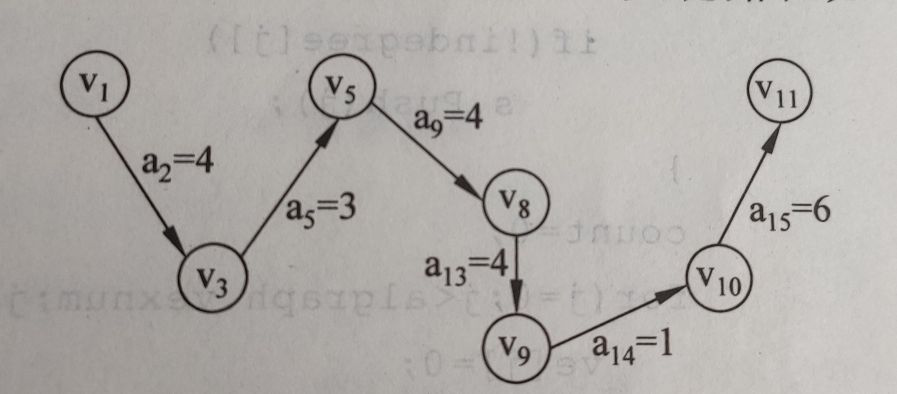
关键路径

下划线的即为关键活动

---

---