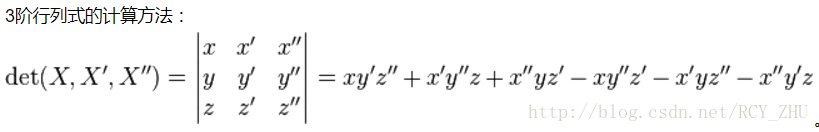51nod1265判断四点共面
第1行:一个数T,表示输入的测试数量(1 <= T <= 1000)
第2 - 4T + 1行:每行4行表示一组数据,每行3个数,x, y, z, 表示该点的位置坐标(-1000 <= x, y, z <= 1000)。
输出共T行,如果共面输出"Yes",否则输出"No"。
1
1 2 0
2 3 0
4 0 0
0 0 0
Yes
题意:中文题
思路:判断四点是否共面问题,点乘和叉乘的应用,任意向量到某一三角形平面的法向量垂直,则四点共面;
还有一种思路是利用行列式:
若行列式为0,则共面;否则不共面。
下面只给出第一种思路的代码:
#include<iostream>
#include<stdio.h>
using namespace std;
typedef long long ll;
struct point
{
double x, y, z;
point operator - (point &o)
{
point ans;
ans.x = this->x - o.x;
ans.y = this->y - o.y;
ans.z = this->z - o.z;
return ans;
}
};
double dot_product(const point &a, const point &b)
{
return a.x * b.x + a.y * b.y + a.z * b.z;
}
point cross_product(const point &a, const point &b)
{
point ans;
ans.x = a.y * b.z - a.z * b.y;
ans.y = a.z * b.x - a.x * b.z;
ans.z = a.x * b.y - a.y * b.x;
return ans;
}
int main()
{
point p[4];
int T;
for (scanf("%d", &T); T--;)
{
for (int i = 0; i < 4; ++i)
{
scanf("%lf%lf%lf", &p[i].x, &p[i].y, &p[i].z);
}
puts(dot_product(p[3] - p[0], cross_product(p[2] - p[0], p[1] - p[0])) == 0.0 ? "Yes\n" : "No\n");
}
return 0;
}
51nod1265判断四点共面的更多相关文章
- 51Nod-1265 四点共面
51Nod 1265 : http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1265 1265 四点共面 基准时间限制:1 秒 ...
- 51nod1265四点共面
1265 四点共面 基准时间限制:1 秒 空间限制:131072 KB 分值: 0 难度:基础题 给出三维空间上的四个点(点与点的位置均不相同),判断这4个点是否在同一个平面内(4点共线也算共面).如 ...
- (四点共面) 51nod1265 四点共面
1265 四点共面 1 秒 131,072 KB 0 分 基础题 给出三维空间上的四个点(点与点的位置均不相同),判断这4个点是否在同一个平面内(4点共线也算共面).如果共面,输出"Ye ...
- 51nod--1265 四点共面 (计算几何基础, 点积, 叉积)
题目: 1265 四点共面 基准时间限制:1 秒 空间限制:131072 KB 分值: 0 难度:基础题 收藏 关注 给出三维空间上的四个点(点与点的位置均不相同),判断这4个点是否在同一个平面内(4 ...
- 51nod1265 四点共面
题目链接:51nod 1265 四点共面 四个点构成的三个向量a,b,c共面的充要条件是存在不全为零的实数x,y,z满足x*a+y*b+z*c=0,然后想到线代了.. 其实就是三个向量的混合积为0:( ...
- 51Nod 1265 四点共面(计算几何)
1265 四点共面 基准时间限制:1 秒 空间限制:131072 KB 分值: 0 难度:基础题 给出三维空间上的四个点(点与点的位置均不相同),判断这4个点是否在同一个平面内(4点共线也算共面). ...
- 51Nod:1265 四点共面
计算几何 修改隐藏话题 1265 四点共面 基准时间限制:1 秒 空间限制:131072 KB 分值: 0 难度:基础题 收藏 关注 给出三维空间上的四个点(点与点的位置均不相同),判断这4个点 ...
- 51nod 1265 四点共面【计算几何+线性代数】
1265 四点共面 基准时间限制:1 秒 空间限制:131072 KB 分值: 0 难度:基础题 收藏 关注 给出三维空间上的四个点(点与点的位置均不相同),判断这4个点是否在同一个平面内(4点共 ...
- 暑假集训#2 div1 J 四点直角 J - Space Invader 四点共面+跨立实验
题意:给你四个点,判断能否先依次通过A,B两点,然后再在某个地方只进行一次直角转弯再一次经过C,D两点: #include <iostream> #include <cstdio&g ...
随机推荐
- Python模块:configparser、hashlib、(subprocess)
configparser模块: 此模块用于生成和修改常见配置文档. 一个常见配置文件(.ini的后缀名)格式如下: [DEFAULT] # DEFAULT 是指后面的字典里都会默认有的内容 Serve ...
- Linux下汇编语言学习笔记17 ---
这是17年暑假学习Linux汇编语言的笔记记录,参考书目为清华大学出版社 Jeff Duntemann著 梁晓辉译<汇编语言基于Linux环境>的书,喜欢看原版书的同学可以看<Ass ...
- BootStrap3栅格系统与布局
栅格系统与布局 Use our powerful mobile-first flexbox grid to build layouts of all shapes and sizes thanks t ...
- openOffice word转pdf,pdf转图片优化版
之前写了一个版本的,不过代码繁琐而且不好用,效率有些问题.尤其pdf转图片速度太慢.下面是优化版本的代码. spriing_boot 版本信息:2.0.1.RELEASE 1.配置信息: packag ...
- Windows 10+Ubuntu 16.04在MBR分区上安装双系统之后没有Windows 10的启动菜单解决方法
背景: 硬盘分区方式:MBR 硬盘容量256,Windows 100,Ubuntu 156,其中主分区安装的是Windows,Ubuntu安装在逻辑分区上,文件系统为Ext4,整个Ubuntu就挂载在 ...
- 【CV论文阅读】+【搬运工】LocNet: Improving Localization Accuracy for Object Detection + A Theoretical analysis of feature pooling in Visual Recognition
论文的关注点在于如何提高bounding box的定位,使用的是概率的预测形式,模型的基础是region proposal.论文提出一个locNet的深度网络,不在依赖于回归方程.论文中提到locne ...
- Websphere优化 (四个方面)举例
Websphere优化 一.简单介绍 环境 名称 版本号 server操作系统 Centos 5.6 应用server操作系统 Windows 7 Websphere版本号 WAS 7.0 数据库 O ...
- BUILD FAILED D:\build.xml:2: 前言中不同意有内容。
1.错误描写叙述 Microsoft Windows [版本号 6.1.7601] 版权全部 (c) 2009 Microsoft Corporation. 保留全部权利. C:\Users\Admi ...
- 怎样用fiddler2捕获移动设备上的http或者https请求
调试移动设备上的问题.看不到发送的请求和得到的响应是比較难过的,fiddler能够实现样的功能. 原理: 在PC上启动fiddler.将手持设备的网络代理改成fiddler. 这样全部的请求和响应都经 ...
- Vijos P1023Victoria的舞会3【贪心+DFS求强联通分量】
链接:Click Me! P1023Victoria的舞会3 Accepted 标签:Victoria的舞会[显示标签] 描写叙述 Victoria是一位颇有成就的艺术家,他因油画作品<我爱北京 ...