POJ1463：Strategic game(树形DP)

Description

Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?

Your program should find the minimum number of soldiers that Bob has to put for a given tree.

For example for the tree:

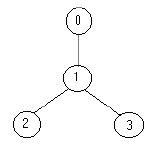
the solution is one soldier ( at the node 1).

Input

The input contains several data sets in text format. Each data set represents a tree with the following description:

• the number of nodes
• the description of each node in the following format
  node_identifier:(number_of_roads) node_identifier₁ node_identifier₂ ... node_identifier_{number_of_roads}
  or
  node_identifier:(0)

The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500);the number_of_roads in each line of input will no more than 10. Every edge appears only once in the input data.

Output

The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following:

Sample Input

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

Sample Output

1
2

题意：给出一棵树，要求找到最少放几个士兵才能将所有点都看守到，每个节点的士兵只能看守临近一个的节点

思路：标准的树形DP，建树的时候要双向都建

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;

int dp[1505][2];
int vis[1505],head[1505];
int len,root;

struct node
{
    int now,next;
} tree[3005];//因为要双向建，所以要开2倍大小

void add(int x,int y)//建树
{
    tree[len].now = y;
    tree[len].next = head[x];
    head[x] = len++;

    tree[len].now = x;
    tree[len].next = head[y];
    head[y] = len++;
}

void dfs(int root)
{
    int i,k;
    vis[root] = 1;
    dp[root][1] = 1;
    dp[root][0] = 0;
    for(i = head[root]; i!=-1; i = tree[i].next)
    {
        k = tree[i].now;
        if(!vis[k])
        {
            dfs(k);
            dp[root][0] += dp[k][1];
            dp[root][1] += min(dp[k][1],dp[k][0]);
        }
    }
}

int main()
{
    int t,x,y,n,i,j;
    while(~scanf("%d",&t))
    {
        len = 0;
        root = -1;
        memset(dp,0,sizeof(dp));
        memset(vis,0,sizeof(vis));
        memset(head,-1,sizeof(head));
        for(j = 1; j<=t; j++)
        {
            scanf("%d:(%d)",&x,&n);
            if(root==-1)
                root = x;
            for(i = 0; i<n; i++)
            {
                scanf("%d",&y);
                add(x,y);
            }
        }
        dfs(root);
        printf("%d\n",min(dp[root][0],dp[root][1]));
    }

    return 0;
}