神经网络优化篇：详解测试时的 Batch Norm（Batch Norm at test time）

Batch归一化将的数据以mini-batch的形式逐一处理，但在测试时，可能需要对每个样本逐一处理，来看一下怎样调整的网络来做到这一点。

回想一下，在训练时，这些就是用来执行Batch归一化的等式。在一个mini-batch中，将mini-batch的\(z^{(i)}\)值求和，计算均值，所以这里只把一个mini-batch中的样本都加起来，用m来表示这个mini-batch中的样本数量，而不是整个训练集。然后计算方差，再算\(z_{\text{norm}}^{(i)}\)，即用均值和标准差来调整，加上\(\varepsilon\)是为了数值稳定性。\(\tilde{z}\)是用\(\gamma\)和\(\beta\)再次调整\(z_{\text{norm}}\)得到的。

请注意用于调节计算的\(\mu\)和\(\sigma^{2}\)是在整个mini-batch上进行计算，但是在测试时，可能不能将一个mini-batch中的6428或2056个样本同时处理，因此需要用其它方式来得到\(\mu\)和\(\sigma^{2}\)，而且如果只有一个样本，一个样本的均值和方差没有意义。那么实际上，为了将的神经网络运用于测试，就需要单独估算\(\mu\)和\(\sigma^{2}\)，在典型的Batch归一化运用中，需要用一个指数加权平均来估算，这个平均数涵盖了所有mini-batch，接下来会具体解释。

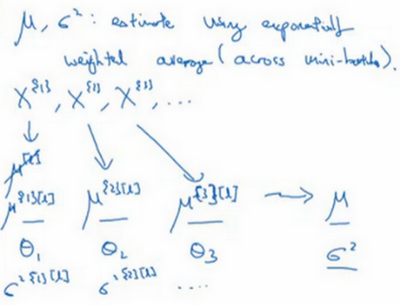
选择\(l\)层，假设有mini-batch，\(X^{[1]}\)，\(X^{[2]}\)，\(X^{[3]}\)……以及对应的\(y\)值等等，那么在为\(l\)层训练\(X^{\{ 1\}}\)时，就得到了\(\mu^{[l]}\)，还是把它写做第一个mini-batch和这一层的\(\mu\)吧，（\(\mu^{[l]} \rightarrow \mu^{\left\{1 \right\}[l]}\)）。当训练第二个mini-batch，在这一层和这个mini-batch中，就会得到第二个\(\mu\)（\(\mu^{\{2\}[l]}\)）值。然后在这一隐藏层的第三个mini-batch，得到了第三个\(\mu\)（\(\mu^{\left\{3 \right\}[l]}\)）值。正如之前用的指数加权平均来计算\(\theta_{1}\)，\(\theta_{2}\)，\(\theta_{3}\)的均值，当时是试着计算当前气温的指数加权平均，会这样来追踪看到的这个均值向量的最新平均值，于是这个指数加权平均就成了对这一隐藏层的\(z\)均值的估值。同样的，可以用指数加权平均来追踪在这一层的第一个mini-batch中所见的\(\sigma^{2}\)的值，以及第二个mini-batch中所见的\(\sigma^{2}\)的值等等。因此在用不同的mini-batch训练神经网络的同时，能够得到所查看的每一层的\(\mu\)和\(\sigma^{2}\)的平均数的实时数值。

最后在测试时，对应这个等式（\(z_{\text{norm}}^{(i)} = \frac{z^{(i)} -\mu}{\sqrt{\sigma^{2} +\varepsilon}}\)），只需要用的\(z\)值来计算\(z_{\text{norm}}^{(i)}\)，用\(\mu\)和\(\sigma^{2}\)的指数加权平均，用手头的最新数值来做调整，然后可以用左边刚算出来的\(z_{\text{norm}}\)和在神经网络训练过程中得到的\(\beta\)和\(\gamma\)参数来计算那个测试样本的\(\tilde{z}\)值。

总结一下就是，在训练时，\(\mu\)和\(\sigma^{2}\)是在整个mini-batch上计算出来的包含了像是64或28或其它一定数量的样本，但在测试时，可能需要逐一处理样本，方法是根据的训练集估算\(\mu\)和\(\sigma^{2}\)，估算的方式有很多种，理论上可以在最终的网络中运行整个训练集来得到\(\mu\)和\(\sigma^{2}\)，但在实际操作中，通常运用指数加权平均来追踪在训练过程中看到的\(\mu\)和\(\sigma^{2}\)的值。还可以用指数加权平均，有时也叫做流动平均来粗略估算\(\mu\)和\(\sigma^{2}\)，然后在测试中使用\(\mu\)和\(\sigma^{2}\)的值来进行所需要的隐藏单元\(z\)值的调整。在实践中，不管用什么方式估算\(\mu\)和\(\sigma^{2}\)，这套过程都是比较稳健的，因此不太会担心具体的操作方式，而且如果使用的是某种深度学习框架，通常会有默认的估算\(\mu\)和\(\sigma^{2}\)的方式，应该一样会起到比较好的效果。但在实践中，任何合理的估算的隐藏单元\(z\)值的均值和方差的方式，在测试中应该都会有效。