蓝桥杯 K好数（Java）

越来越觉得自己菜，一道简单的动态规划写不出来，题解也是看了很多份才看懂了，所以尽量以图表的方式写了题解，希望我的题解能帮到其他人吧。(;´Д`)

首先是题目：

输入描述:

输入包含两个正整数，K和L。

输入样例:

4 2

输出描述:

输出一个整数，表示答案对1000000007取模后的值。

输出样例:

7

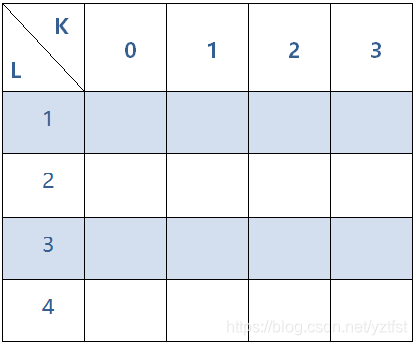
1.首先我们初始化一个L行K列的数组（题目输入为4 2，所以先以4进制为例子，位数不限制）

用于表示

在L位的情况下，最后一位为K的符合条件的数字的个数

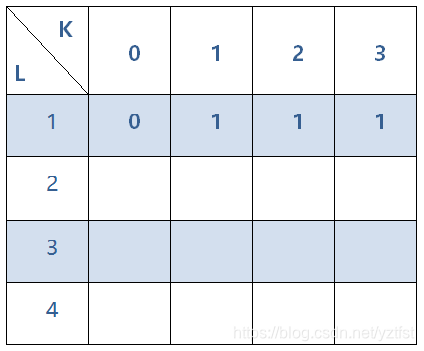
2.

四进制的情况下每一位能取的值为0到3

因为不能以0作为第一位数（因为后面计算两位数时出现00，02，03这种并不是两位数）

所以以0为第一位的有0种，以1为第一位的有1种，以2为第一位的有1种，以3为第一位的有1种，结果为0，1，1，1



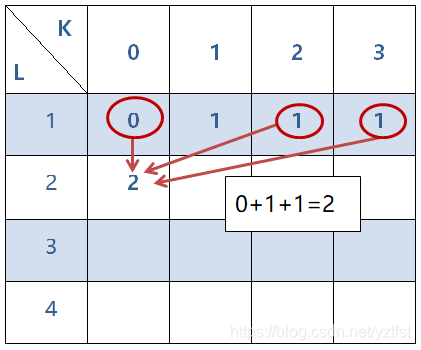
3.两位数的以0结尾的数有20和30，因为10相邻不满足条件，

所以此时以0结尾的数的数量为2，

也就是在第二位为0的情况下，把第一位除了等于1以外的所有可能相加

（虽然把00这种不应该有的可能也加上去了，但是由于它本来就是0，所以不会有影响）



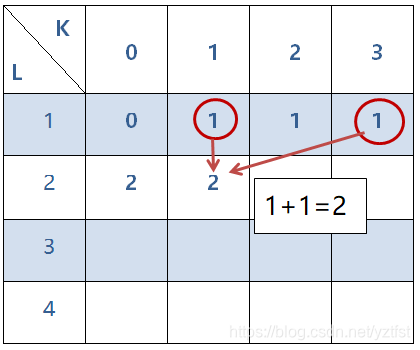
4.两位数的以1结尾的数有11和31，因为21相邻不满足条件，

所以此时以1结尾的数的数量为2，

也就是在第二位为1的情况下，把第一位除了等于0和2以外的所有可能相加



5.同理得到两位数的以0，1，2，3结尾的所有可能



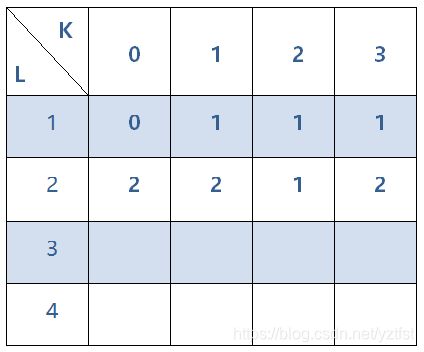
6.接下来是三位数，

三位数的以0结尾的数只要考虑第2,第3位，也就是最后两位不会出现相邻的情况就可以了

所以和第三步同样在第三位为0的情况下，把第二位除了等于1以外的所有可能相加



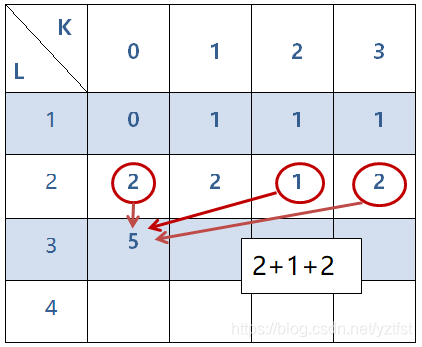
7.最后是完整的表格



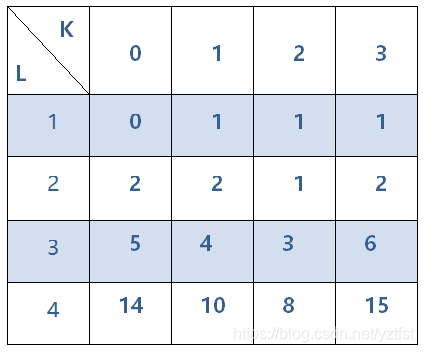
8.最后把第四行的14，10，8，15加起来就得到在4进制的情况下，四位数的K好数的数量（把第二行的加起来就是题目样例4 2的结果7）

接下来是代码：

import java.math.BigInteger;
import java.util.Scanner;

public class Kgood {
	public static BigInteger getNumberOfKGood(int l, int k) {
		// 这是第一步定义的表格的二维数组
		int [][] array = new int[l][k];
		// 这是第二步的初始化，将一位的情况的结果设置为0,1,1,1......
		for (int i = 1; i < k; i++) {
			array[0][i] = 1;
		}

		// i代表表格的行，也就是位数
		// j代表表格的列，也就是可能取的进制数
		for (int i = 1; i < l; i++) {
			for (int j = 0; j < k; j++) {
				// 这里为第三步，也就是把这一位所能取的值遍历，并与上一位j做比较，筛选掉相邻的可能
				for (int j2 = 0; j2 < k; j2++) {
					if ((j != j2 + 1) && (j != j2 - 1)) {
						// 按题目要求取模
						array[i][j] = (array[i][j] + array[i-1][j2]) % 1000000007;
					}
				}
			}
		}

		// 最后一步的取值，把最后一行的值加起来就是了
		// 因为数据挺大的，所以遇事不决用大数[滑稽]
		BigInteger sum = new BigInteger("0");
		for (int i = 0; i < k; i++) {
			sum = sum.add(new BigInteger(Integer.toString(array[l - 1][i])));
		}
		return sum.mod(new BigInteger("1000000007"));
	}

	public static void main(String[] args) {

		Scanner sc = new Scanner(System.in);
		int k = sc.nextInt();
		int l = sc.nextInt();

		BigInteger sum = getNumberOfKGood(l, k);

		System.out.println(sum);

		sc.close();
	}
}