生成式学习算法（三）之----高斯判别分析模型（Gaussian Discriminant Analysis ，GDA）

高斯判别分析模型（Gaussian Discriminant Analysis ，GDA）

当我们分类问题的输入特征$x $为连续值随机变量时，可以用高斯判别分析模型（Gaussian Discriminant Analysis ，GDA）。高斯判别分析模型通过多元正态分布来建模前面提到的概率 \(p(x | y)\)。具体的，这个模型为，
\[
\begin{equation}
\begin{aligned}
y & \sim \operatorname{Bernoulli}(\phi) \\
x | y=0 & \sim \mathcal{N}\left(\mu_{0}, \Sigma\right) \\
x | y=1 & \sim \mathcal{N}\left(\mu_{1}, \Sigma\right)
\end{aligned}
\end{equation}
\]

这个模型中的参数有 \(\phi, \Sigma, \mu_{0}\) 和 \(\mu_{1}\) 。注意到，尽管有两个不同的均值向量 \(\mu_{0}\) 和 \(\mu_{1}\)。但模型通常只有只用一个协方差矩阵 $ \Sigma$。将这三个随机变量的分布写出来则有，
\[
\begin{equation}
\begin{aligned}
p(y) &=\phi^{y}(1-\phi)^{1-y} \\
p(x | y=0) &=\frac{1}{(2 \pi)^{n / 2}|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}\left(x-\mu_{0}\right)^{T} \Sigma^{-1}\left(x-\mu_{0}\right)\right) \\
p(x | y=1) &=\frac{1}{(2 \pi)^{n / 2}|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}\left(x-\mu_{1}\right)^{T} \Sigma^{-1}\left(x-\mu_{1}\right)\right)
\end{aligned}
\end{equation}
\]
有了上面三个分布，则可以知道数据的对数似然概率\(\ell\)为，
\[
\begin{equation}
\begin{aligned}
\ell\left(\phi, \mu_{0}, \mu_{1}, \Sigma\right) &=\log \prod_{i=1}^{m} p\left(x^{(i)}, y^{(i)} ; \phi, \mu_{0}, \mu_{1}, \Sigma\right) \\
&=\log \prod_{i=1}^{m} p\left(x^{(i)} | y^{(i)} ; \mu_{0}, \mu_{1}, \Sigma\right) p\left(y^{(i)} ; \phi\right)
\end{aligned}
\end{equation}
\]

通过求各个参数关于对数似然概率\(\ell\)偏导为零的值，也就是使各个参数在这些取值下使得对数似然概率\(\ell\)最大的值，可以找到个参数的最大似然估计为，
\[
\begin{equation}
\begin{aligned}
\phi &=\frac{1}{m} \sum_{i=1}^{m} 1\left\{y^{(i)}=1\right\} \\
\mu_{0} &=\frac{\sum_{i=1}^{m} 1\left\{y^{(i)}=0\right\} x^{(i)}}{\sum_{i=1}^{m} 1\left\{y^{(i)}=0\right\}} \\
\mu_{1} &=\frac{\sum_{i=1}^{m} 1\left\{y^{(i)}=1\right\} x^{(i)}}{\sum_{i=1}^{m} 1\left\{y^{(i)}=1\right\}} \\
\Sigma &=\frac{1}{m} \sum_{i=1}^{m}\left(x^{(i)}-\mu_{y^{(i)}}\right)\left(x^{(i)}-\mu_{y^{(i)}}\right)^{T}
\end{aligned}
\end{equation}
\]
给定训练数据，通过高斯判别分析训练出的模型可以由下图来表示。其中圈和叉分别为两类数据。两个等高线图则是根据上式用数据拟合出的两个最优密度分布。直线为等高线密度相等的点，皆为0.5，也就是所谓决策边界。由于这两个分部共享协方差阵，所以虽然他们密度的均值不同，但形状相同。

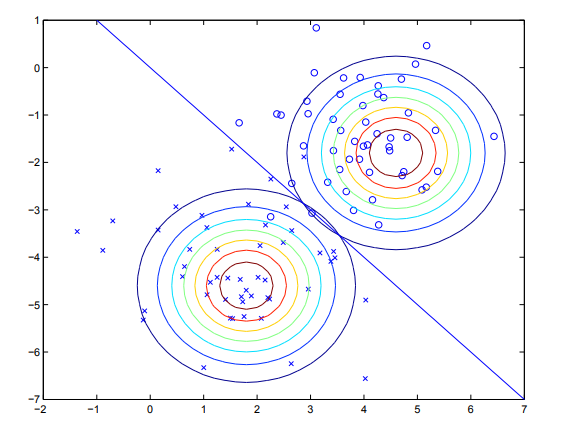
高斯判别分析模型和logistic回归模型之间的关系

如果我们将后验概率$p\left(y^{(i)}=1 |x^{(i)} ; \phi, \mu_{0}, \mu_{1}, \Sigma\right) $ 视为 $x $ 的函数，则高斯判别分析模型可以写成和logistic回归模型一样的形式，即有
\[
p\left(y=1 | x ; \phi, \Sigma, \mu_{0}, \mu_{1}\right)=\frac{1}{1+\exp \left(-\theta^{T} x\right)}
\]
这里$ \theta$ 是模型参数的函数。$ x$ 为 $ n+1$ 维的带常数截距项的特征向量。

需要注意的是虽然两个模型具有相同的形式，在相同的数据集上训练这两个模型一般得到的是两个不同的决策边界。那么问题就来了，我们什么时候该用什么模型？哪个模型更好呢？

我们刚才的讨论已经说明了，如果$ x$ 的条件分布\(p(x | y)\) 满足多元高斯分布，则后验概率表达式\(p(y | x)\) 一定是logistic回归函数的形式，但反过来不一定是正确的。即在后验概率表达后验概率\(p(y | x)\) 是logistic回归函数的形式的条件下，$ x$ 的条件概率分布\(p(x | y)\) 不一定满足多元高斯分布。
这表明了GDA模型对数据的模型假设要比logistic回归模型强。
当模型假设正确的时候，也就是\(p(x | y)\) 确实满足多元高斯正态分布的时候，GDA模型是一个更好的模型，是渐进有效的（在更准意义下，没有其它模型能比它更好）。
然而，通过做出较弱的模型假设，logistic回归模型更鲁棒，对于不正确的模型假设也不那么敏感。例如当X满足泊松分布时也能推导出logistic回归模型，但这时如果用GDA模型来拟合数据，则会得到较差的效果。
综上所述，logistic回归模型作出的假设更弱，对于不正确的假设也更鲁棒。在数据集规模够大的情况下，logistic回归模型几乎总是要优于GDA模型。GDA模型通过做出更强的假设对数据的利用效率更高，也就是说当假设正确或近似正确时能以较少的数据拟合出较好的模型。
最后严正声明：logistic回归模型是判别式模型，高斯判别分析模型（GDA）是生成式模型。