大O表示法

概念

大O表示法是和数据项的个数相关联的粗略度量算法时间复杂度的快捷方法。

---

常数
一个无序可重复数组插入一个数据项的时间T是常数K，常数K表示一次插入所花费的时间，包含cpu、编译器等工作时间。
可表示为：T = K

线性查找
从数组中线性查找一个数据项平均需要N/2步，每步所花费的时间为K
可表示为：T = K*N/2
常数2可以并入K
进而可以表示为：T = K*N

二分查找
从一个有序数组中二分查找一个数据项平均需要log2(N)步，每步所花费的时间为K
可表示为：T = K*log2(N)
因为所有对数和其他对数都成比例，比如，从底数是2转换为底数是10需乘以3.322，所以可以将底数常数并入K
进而可以表示为：T = K*log(N)

---

大O表示法

大O表示法和上面的公式比较类似，但它省去了常数K。因为我们并不在乎具体的微处理器或编译器；真正需要比较的是对应不同的N值，T是如何变化的，而不是具体的数字。
大O表示法使用大写字母O，其含义是"order of"——大约的意思。
无序可重复数组插入一个数据项表示为——O(1)
线性查找表示为——O(N)
二分查找表示为——O(log N)
冒泡排序比较和交换都是——O(N²)

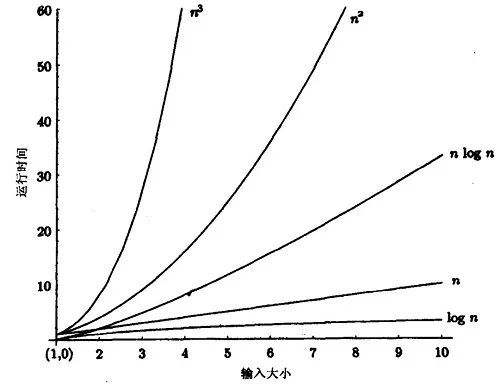
O(1)<O(log n)<O(n)<O(n log n)<O(n²)<O(n³)