《DSP using MATLAB》Problem 8.31


代码:
%% ------------------------------------------------------------------------
%% Output Info about this m-file
fprintf('\n***********************************************************\n');
fprintf(' <DSP using MATLAB> Problem 8.31 \n\n'); banner();
%% ------------------------------------------------------------------------ Fp = 3.2; % analog passband freq in kHz 6.4 kpi
Fs = 3.8; % analog stopband freq in kHz 7.6 kpi
fs = 8; % sampling rate in kHz 16.0 kpi % -------------------------------
% Ω=(2/T)tan(ω/2)
% ω=2*[atan(ΩT/2)]
% Digital Filter Specifications:
% -------------------------------
wp = 2*pi*Fp/fs % digital passband freq in rad 0.8pi
%wp = Fp;
ws = 2*pi*Fs/fs % digital stopband freq in rad 0.95pi
%ws = Fs;
Rp = 0.5; % passband ripple in dB
As = 45; % stopband attenuation in dB Ripple = 10 ^ (-Rp/20) % passband ripple in absolute
Attn = 10 ^ (-As/20) % stopband attenuation in absolute % Analog prototype specifications: Inverse Mapping for frequencies
T = 1/8000; % set T = 1
%fs = 1/T;
OmegaP = (2/T)*tan(wp/2) % prototype passband freq 1.9593pi 15675pi
OmegaS = (2/T)*tan(ws/2) % prototype stopband freq 8.089pi 64712pi % Analog Chebyshev-1 Prototype Filter Calculation:
[cs, ds] = afd_chb1(OmegaP, OmegaS, Rp, As); % Calculation of second-order sections:
fprintf('\n***** Cascade-form in s-plane: START *****\n');
[CS, BS, AS] = sdir2cas(cs, ds)
fprintf('\n***** Cascade-form in s-plane: END *****\n'); % Calculation of Frequency Response:
[db_s, mag_s, pha_s, ww_s] = freqs_m(cs, ds, 8*pi/T); % --------------------------------------------------------------------
% find exact band-edge frequencies for the given dB specifications
% --------------------------------------------------------------------
[diff_to_45dB, ind] = min(abs(db_s+45))
db_s(ind-3 : ind+3) % magnitude response, dB ww_s(ind)/(pi) % analog frequency in kpi units
%ww_s(ind)/(2*pi) % analog frequency in Hz units [sA,index] = sort(abs(db_s+45));
AA_dB = db_s(index(1:8))
AB_rad = ww_s(index(1:8))/(pi)
AC_Hz = ww_s(index(1:8))/(2*pi)
% ------------------------------------------------------------------- % Calculation of Impulse Response:
[ha, x, t] = impulse(cs, ds); % Impulse Invariance Transformation:
%[b, a] = imp_invr(cs, ds, T); % Bilinear Transformation
[b, a] = bilinear(cs, ds, 1/T)
[C, B, A] = dir2cas(b, a) % Calculation of Frequency Response:
[db, mag, pha, grd, ww] = freqz_m(b, a); % --------------------------------------------------------------------
% find exact band-edge frequencies for the given dB specifications
% --------------------------------------------------------------------
[diff_to_45dB, ind] = min(abs(db+45))
db(ind-3 : ind+3) % magnitude response, dB ww(ind)/(pi) (2/T)*tan(ww(ind)/2)/pi [sA,index] = sort(abs(db+45));
AA_dB = db(index(1:8))'
AB_rad = ww(index(1:8))'/pi
AC_Hz = (2/T)*tan(ww(index(1:8))'/2)/pi
% ------------------------------------------------------------------- %% -----------------------------------------------------------------
%% Plot
%% -----------------------------------------------------------------
figure('NumberTitle', 'off', 'Name', 'Problem 8.31 Analog Chebyshev-I lowpass')
set(gcf,'Color','white');
M = 1.0; % Omega max subplot(2,2,1); plot(ww_s/pi, mag_s); grid on; %axis([-10, 10, 0, 1.2]);
xlabel(' Analog frequency in \piHz units'); ylabel('|H|'); title('Magnitude in Absolute');
% set(gca, 'XTickMode', 'manual', 'XTick', [-8.089, -1.9593, 0, 1.9593, 8.089]); % T = 1
set(gca, 'XTickMode', 'manual', 'XTick', [-80000, -64712, -15675, 0, 15675, 64712, 80000]); % T = 1/8000
set(gca, 'YTickMode', 'manual', 'YTick', [0, 0.006, 0.94, 1.0, 1.5]); subplot(2,2,2); plot(ww_s/pi, db_s); grid on; %axis([0, M, -50, 10]);
xlabel('Analog frequency in \piHz units'); ylabel('Decibels'); title('Magnitude in dB ');
% set(gca, 'XTickMode', 'manual', 'XTick', [-8.089, -1.9593, 0, 1.9593, 5.7, 8.089]); % T = 1
set(gca, 'XTickMode', 'manual', 'XTick', [-80000, -64712, -15675, 0, 15675, 45696, 64712, 80000]); % T = 1/8000
set(gca, 'YTickMode', 'manual', 'YTick', [-45, -1, 0]);
set(gca,'YTickLabelMode','manual','YTickLabel',['45';' 1';' 0']); subplot(2,2,3); plot(ww_s/pi, pha_s/pi); grid on; %axis([-10, 10, -1.2, 1.2]);
xlabel('Analog frequency in \piHz nuits'); ylabel('radians'); title('Phase Response');
% set(gca, 'XTickMode', 'manual', 'XTick', [-8.089, -1.9593, 0, 1.9593, 8.089]); % T = 1
set(gca, 'XTickMode', 'manual', 'XTick', [-80000, -64712, -15675, 0, 15675, 45696, 64712, 80000]); % T = 1/8000
set(gca, 'YTickMode', 'manual', 'YTick', [-1:0.5:1]); subplot(2,2,4); plot(t, ha); grid on; %axis([0, 30, -0.05, 0.25]);
xlabel('time in seconds'); ylabel('ha(t)'); title('Impulse Response'); figure('NumberTitle', 'off', 'Name', 'Problem 8.31 Digital Chebyshev-I lowpass')
set(gcf,'Color','white');
M = 2; % Omega max subplot(2,2,1); plot(ww/pi, mag); axis([0, M, 0, 1.2]); grid on;
xlabel(' Digital frequency in \pi units'); ylabel('|H|'); title('Magnitude Response');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.8, 0.95, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [0, 0.0056, 0.9441, 1]); subplot(2,2,2); plot(ww/pi, pha/pi); axis([0, M, -1.1, 1.1]); grid on;
xlabel('Digital frequency in \pi nuits'); ylabel('radians in \pi units'); title('Phase Response');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.8, 0.95, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [-1:1:1]); subplot(2,2,3); plot(ww/pi, db); axis([0, M, -80, 10]); grid on;
xlabel('Digital frequency in \pi units'); ylabel('Decibels'); title('Magnitude in dB ');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.8, 0.93, 0.95, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [-70, -45, -1, 0]);
set(gca,'YTickLabelMode','manual','YTickLabel',['70';'45';' 1';' 0']); subplot(2,2,4); plot(ww/pi, grd); grid on; %axis([0, M, 0, 35]);
xlabel('Digital frequency in \pi units'); ylabel('Samples'); title('Group Delay');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.8, 0.95, M]);
%set(gca, 'YTickMode', 'manual', 'YTick', [0:5:35]); figure('NumberTitle', 'off', 'Name', 'Problem 8.31 Pole-Zero Plot')
set(gcf,'Color','white');
zplane(b,a);
title(sprintf('Pole-Zero Plot'));
%pzplotz(b,a); % ----------------------------------------------
% Calculation of Impulse Response
% ----------------------------------------------
figure('NumberTitle', 'off', 'Name', 'Problem 8.31 Imp & Freq Response')
set(gcf,'Color','white');
t = [0: 0.000005 : 8*0.0001]; subplot(2,1,1); impulse(cs,ds,t); grid on; % Impulse response of the analog filter
axis([0, 8*0.0001, -1.5*10000, 2.0*10000]);hold on n = [0:1:7*0.0001/T]; hn = filter(b,a,impseq(0,0,7*0.0001/T)); % Impulse response of the digital filter
stem(n*T,hn); xlabel('time in sec'); title (sprintf('Impulse Responses T=%2d',T));
hold off % Calculation of Frequency Response:
[dbs, mags, phas, wws] = freqs_m(cs, ds, 8*pi/T); % Analog frequency s-domain [dbz, magz, phaz, grdz, wwz] = freqz_m(b, a); % Digital z-domain %% -----------------------------------------------------------------
%% Plot
%% ----------------------------------------------------------------- subplot(2,1,2); plot(wws/(2*pi), mags/T, 'b+', wwz/(2*pi*T), magz, 'r'); grid on; xlabel('frequency in Hz'); title('Magnitude Responses'); ylabel('Magnitude'); text(-0.8,0.15,'Analog filter', 'Color', 'b'); text(0.6,1.05,'Digital filter', 'Color', 'r'); %% -----------------------------------------------------------------------
%% MATLAB cheby1 function
%% ----------------------------------------------------------------------- % Analog Prototype Order Calculations:
ep = sqrt(10^(Rp/10)-1); % Passband Ripple Factor
A = 10^(As/20); % Stopband Attenuation Factor
OmegaC = OmegaP; % Analog Chebyshev-1 prototype cutoff freq
OmegaR = OmegaS/OmegaP; % Analog prototype Transition ratio
g = sqrt(A*A-1)/ep; % Analog prototype Intermediate cal N = ceil(log10(g+sqrt(g*g-1))/log10(OmegaR+sqrt(OmegaR*OmegaR-1)));
fprintf('\n\n ********** Chebyshev-I Filter Order = %3.0f \n', N) % Digital Chebyshev-1 Filter Design:
wn = wp/pi; % Digital Chebyshev-1 cutoff freq in pi units [b, a] = cheby1(N, Rp, wn)
[C, B, A] = dir2cas(b, a) % Calculation of Frequency Response:
[db, mag, pha, grd, ww] = freqz_m(b, a); % --------------------------------------------------------------------
% find exact band-edge frequencies for the given dB specifications
% --------------------------------------------------------------------
[diff_to_45dB, ind] = min(abs(db+45))
db(ind-3 : ind+3) % magnitude response, dB ww(ind)/(pi) (2/T)*tan(ww(ind)/2)/pi [sA,index] = sort(abs(db+45));
AA_dB = db(index(1:8))'
AB_rad = ww(index(1:8))'/pi
AC_Hz = (2/T)*tan(ww(index(1:8))'/2)/pi
% ------------------------------------------------------------------- %% -----------------------------------------------------------------
%% Plot
%% ----------------------------------------------------------------- figure('NumberTitle', 'off', 'Name', 'Problem 8.31 Digital Chebyshev-I lowpass by cheby1 function')
set(gcf,'Color','white');
M = 2; % Omega max subplot(2,2,1); plot(ww/pi, mag); axis([0, M, 0, 1.2]); grid on;
xlabel('Digital frequency in \pi units'); ylabel('|H|'); title('Magnitude Response');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.8, 0.95, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [0, 0.0056, 0.9441, 1]); subplot(2,2,2); plot(ww/pi, pha/pi); axis([0, M, -1.1, 1.1]); grid on;
xlabel('Digital frequency in \pi nuits'); ylabel('radians in \pi units'); title('Phase Response');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.8, 0.95, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [-1:1:1]); subplot(2,2,3); plot(ww/pi, db); axis([0, M, -100, 10]); grid on;
xlabel('Digital frequency in \pi units'); ylabel('Decibels'); title('Magnitude in dB ');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.8, 0.93, 0.95, M]);
set(gca, 'YTickMode', 'manual', 'YTick', [-60, -45, -1, 0]);
set(gca,'YTickLabelMode','manual','YTickLabel',['60';'45';' 1';' 0']); subplot(2,2,4); plot(ww/pi, grd); grid on; %axis([0, M, 0, 35]);
xlabel('Digital frequency in \pi units'); ylabel('Samples'); title('Group Delay');
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.8, 0.95, M]);
%set(gca, 'YTickMode', 'manual', 'YTick', [0:5:35]); figure('NumberTitle', 'off', 'Name', 'Problem 8.31 Pole-Zero Plot')
set(gcf,'Color','white');
zplane(b,a);
title(sprintf('Pole-Zero Plot'));
%pzplotz(b,a); % ----------------------------------------------
% Calculation of Impulse Response
% ----------------------------------------------
figure('NumberTitle', 'off', 'Name', 'Problem 8.31 Imp & Freq Response')
set(gcf,'Color','white');
t = [0: 0.000005 : 8*0.0001]; subplot(2,1,1); impulse(cs,ds,t); grid on; % Impulse response of the analog filter
axis([0, 8*0.0001, -1.5*10000, 2.0*10000]);hold on n = [0:1:7*0.0001/T]; hn = filter(b,a,impseq(0,0,7*0.0001/T)); % Impulse response of the digital filter
stem(n*T,hn); xlabel('time in sec'); title (sprintf('Impulse Responses T=%2d',T));
hold off % Calculation of Frequency Response:
[dbs, mags, phas, wws] = freqs_m(cs, ds, 8*pi/T); % Analog frequency s-domain [dbz, magz, phaz, grdz, wwz] = freqz_m(b, a); % Digital z-domain %% -----------------------------------------------------------------
%% Plot
%% ----------------------------------------------------------------- subplot(2,1,2); plot(wws/(2*pi), mags/T, 'b+', wwz/(2*pi*T), magz, 'r'); grid on; xlabel('frequency in Hz'); title('Magnitude Responses'); ylabel('Magnitude'); text(-0.8,0.15,'Analog filter', 'Color', 'b'); text(0.6,1.05,'Digital filter', 'Color', 'r');
运行结果:
这里放上T=1/8000sec的结果。
模拟chebyshev-1型低通,幅度谱、相位谱和脉冲响应
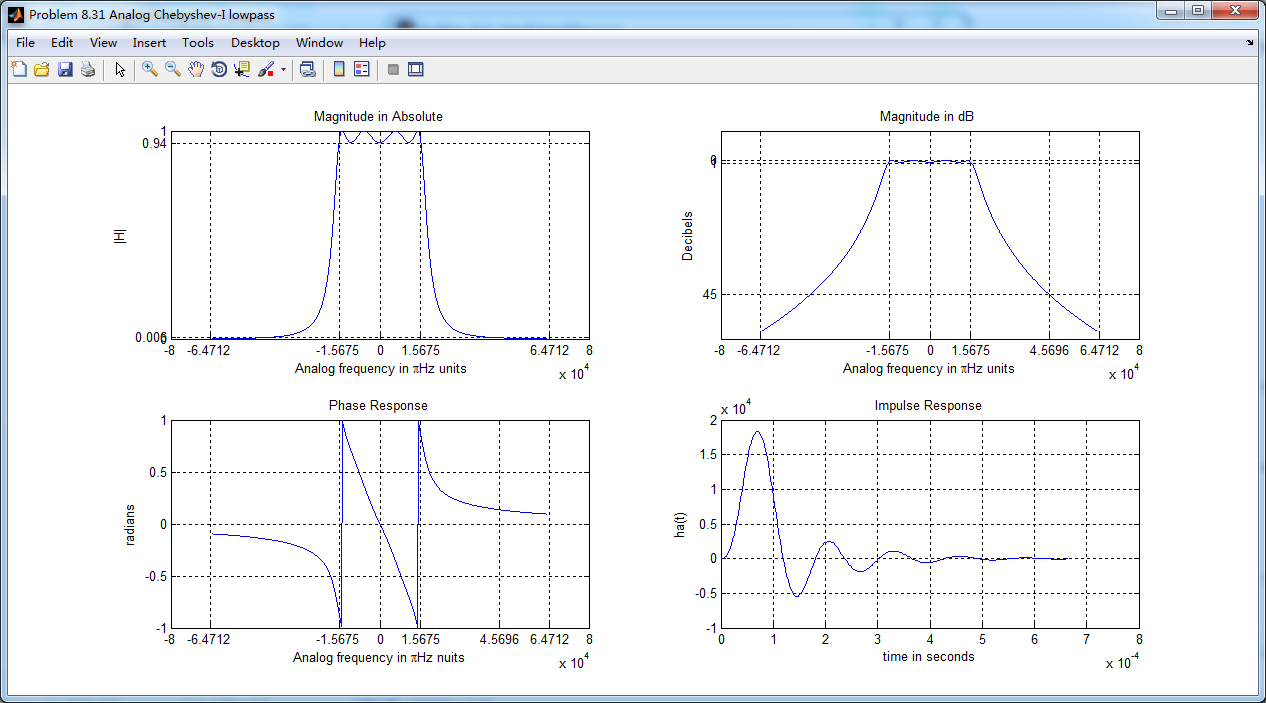
采用双线性变换法,得到数字chebyshev-1型低通滤波器,幅度谱、相位谱和群延迟响应
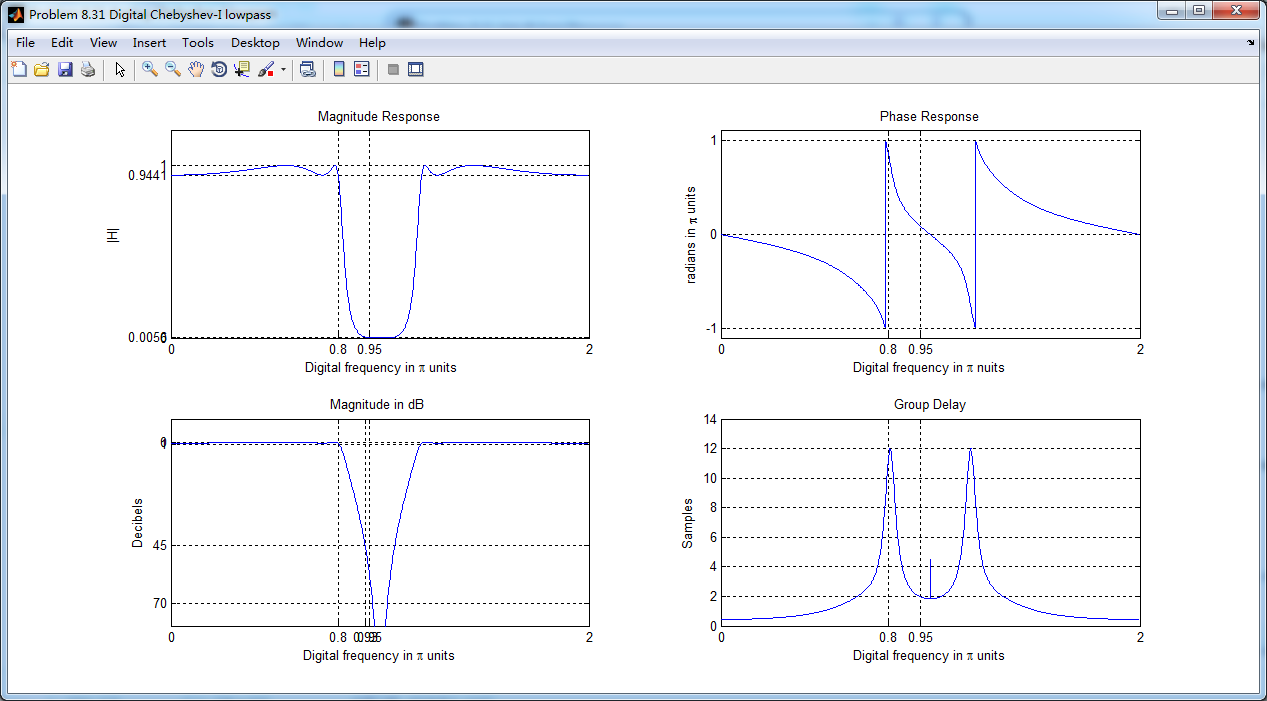
采用MATLAB自带cheby1函数得到的数字低通,其幅度谱、相位谱和群延迟

cheby1函数得到的数字低通,和相应的模拟原型的脉冲响应,二者形态不同。
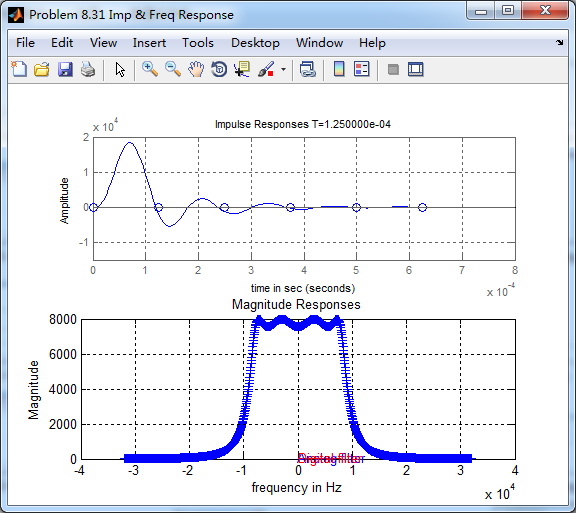
《DSP using MATLAB》Problem 8.31的更多相关文章
- 《DSP using MATLAB》Problem 5.31
第3小题: 代码: %% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ %% Out ...
- 《DSP using MATLAB》Problem 7.31
参照Example7.27,因为0.1π=2πf1 f1=0.05,0.9π=2πf2 f2=0.45 所以0.1π≤ω≤0.9π,0.05≤|H|≤0.45 代码: %% +++++++++ ...
- 《DSP using MATLAB》Problem 7.26
注意:高通的线性相位FIR滤波器,不能是第2类,所以其长度必须为奇数.这里取M=31,过渡带里采样值抄书上的. 代码: %% +++++++++++++++++++++++++++++++++++++ ...
- 《DSP using MATLAB》Problem 7.25
代码: %% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ %% Output In ...
- 《DSP using MATLAB》Problem 7.24
又到清明时节,…… 注意:带阻滤波器不能用第2类线性相位滤波器实现,我们采用第1类,长度为基数,选M=61 代码: %% +++++++++++++++++++++++++++++++++++++++ ...
- 《DSP using MATLAB》Problem 6.12
代码: %% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ %% Output In ...
- 《DSP using MATLAB》Problem 6.10
代码: %% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ %% Output In ...
- 《DSP using MATLAB》Problem 2.7
1.代码: function [xe,xo,m] = evenodd_cv(x,n) % % Complex signal decomposition into even and odd parts ...
- 《DSP using MATLAB》Problem 2.6
1.代码 %% ------------------------------------------------------------------------ %% Output Info abou ...
随机推荐
- vue sChart组件使用页面一片空白问题及示例
参考:https://www.ctolib.com/mip/lin-xin-vue-schart.html 在网上其他示例里,我试验后发现:渲染到<canvas id="myChart ...
- ionic js 加载动画 ionSpinner 提供了许多种旋转加载的动画图标。当你的界面加载时,你就可以呈现给用户相应的加载图标。 该图标采用的是SVG
ionic 加载动画 ion-spinner ionSpinner 提供了许多种旋转加载的动画图标.当你的界面加载时,你就可以呈现给用户相应的加载图标. 该图标采用的是SVG. 用法 <ion- ...
- ArcGIS Server 10.x查询管理用户名和修改管理员密码
在x:\Program Files\ArcGIS\Server\tools\passwordreset下有个bat文件,用管理员用户运行它. PasswordReset -l PasswordRese ...
- mkdir: Cannot create directory /file. Name node is in safe mode.
刚刚在hadoop想创建一个目录的时候,发现报错了 具体信息如下: [hadoop@mini1 hadoop-2.6.4]$ hadoop fs -mkdir /file mkdir: Cannot ...
- 爬虫-Requests 使用入门
requests 的底层实现其实就是 urllib json在线解析工具 ---------------------------------------------- Linux alias命令用于设 ...
- LUOGU P4322 [JSOI2016]最佳团体(0/1分数规划+树形背包)
传送门 解题思路 一道0/1分数规划+树上背包,两个应该都挺裸的,话说我常数为何如此之大..不吸氧洛谷过不了啊. 代码 #include<iostream> #include<cst ...
- 2019/11/1 CSP模拟
写在前面的反思 该拿的部分分还是得拿完啊,因为懒+动作慢没有写最后一道题的菊花图和链的情况,其实这两个点并不难.. 虽然只有\(10pts\),但是已经足够往上爬一截了啊,额外的\(10pts\)在今 ...
- redis可视化客户端工具TreeNMS
TreeNMS是一款redis,Memcache可视化客户端工具,采用JAVA开发,实现基于WEB方式对Redis, Memcached数据库进行管理.维护. 功能包括:状态参数监控,NoSQL数据库 ...
- CSS display overflow 属性 cursor光标类型
display属性 功能:规则网页元素如何显示的问题. 取值:none(隐藏).block(以块元素显示).inline(以行内元素显示) block:可以实现将行内元素转成块元素. ...
- Bzoj 1036 树的统计 分类: ACM TYPE 2014-12-29 18:55 72人阅读 评论(0) 收藏
Description 一棵树上有n个节点,编号分别为1到n,每个节点都有一个权值w.我们将以下面的形式来要求你对这棵树完成一些操作: I. CHANGE u t : 把结点u的权值改为t II. Q ...
