ng机器学习视频笔记（一）——线性回归、代价函数、梯度下降基础

ng机器学习视频笔记（一）

——线性回归、代价函数、梯度下降基础

（转载请附上本文链接——linhxx）

一、线性回归

线性回归是监督学习中的重要算法，其主要目的在于用一个函数表示一组数据，其中横轴是变量（假定一个结果只由一个变量影响），纵轴是结果。

线性回归得到的方程，称为假设函数（Hypothesis Function）。当假设函数是线性函数时，其公式为：

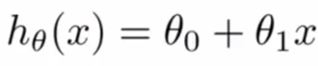
二、代价函数

代价函数是用于评价线性回归，其公式为：

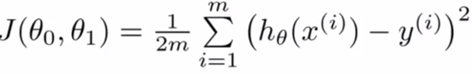
计算方式是计算每一个点在当前假设函数情况下，偏差的平方和，再取平均数。m即表示一共取了几个点进行判断。

因此可知，假设函数预计的越准确的，其代价函数的结果越接近于0。对于不同的假设函数，其J的结果可以形成一个轮廓图，如下：

上图中，横坐标θ0表示与y轴的交点，纵坐标θ1表示斜率。同一个圆环，表示取值在这些范围内的假设函数，其代价函数的结果是一样的，即这些取值情况下的精度是一样的。

三、梯度下降算法

梯度下降（Gradient descent）是获取代价函数最小值的过程。

1、思想

想象现在在一座山（三维立体图形），有多个山峰和山谷（极大值和极小值）。当你在某个位置，找到最快下山的路线（偏导数最小而且是负数的方向），并走一小步，然后接着寻找最快下山的路线，直到到达最低点。

2、存在问题

从上述思想可知，对于有多个极小值情况下，用梯度下降算法很有可能到不了最小值点，只会到达某个极小值点，就因为周围没有减小的路线，而停止。

因此，不同的起始值，最终得到的结果会不一样。

3、步骤

如下述公式：（图片来自视频课程）

其中，α就是“一小步”的距离，α取的大小的变化，会导致从一个点抵达的下一个点的位置不一样，会影响到最终抵达的位置。

不断的执行公式，最终会抵达一个结果。

要求：每次更新的时候，θ1和θ0都要更新，即将θ0和θ1的结果都算出来后，才更新θ0和θ1的值，进行下一次的计算。图中的“:=”符号，即赋值符号，对于大多数编程语言来说，就是=号。

——written by linhxx

更多最新文章，欢迎关注微信公众号“决胜机器学习”，或扫描右边二维码。