normal equation（正规方程）

normal equation（正规方程）

• 正规方程是通过求解下面的方程来找出使得代价函数最小的参数的：

\[\frac{\partial}{\partial\theta_j}J\left(\theta\right)=0
\]

• 假设我们的训练集特征矩阵为 \(X\)（包含了\(x_0=1\)）并且我们的训练集结果为向量 \(y\)，则利用正规方程解出向量：

\[\theta ={{\left( {X^T} X \right)}^{-1}}{X^T}y
\]

• 梯度下降与正规方程的比较：
  • 梯度下降：需要选择学习率\(\alpha\)；需要多次迭代；当特征数量n大时也能较好适用，适用于各种类型的模型；
  • 正规方程：不需要选择学习率\(\alpha\)；不需要迭代，一次运算就可以得出\(\theta\)的最优解；需要计算\({\left( {X^T} X \right)}^{-1}\)；如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为\(O(n^3)\)，通常来说当n小于10000时还是可以接受的，只适用于线性模型，不适合逻辑回归模型等其他模型。

编程实现

在编程作业1.1：单变量线性回归的基础上实现：

# 正规方程
def normalEqn(X, y):
    theta = np.linalg.inv(X.T@X)@X.T@y  #X.T@X等价于X.T.dot(X)；np.linalg.inv()：矩阵求逆
    return theta

final_theta2=normalEqn(X, y)#感觉和批量梯度下降的theta的值有点差距
final_theta2

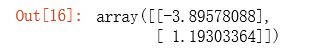
在之前运行完梯度下降算法之后，我们输出\(\theta\)的值如下：

可以看出两种方法求出的\(\theta\)值基本相似。