[HNOI 2010]Planar

Description

题库链接

给出 \(T\) 个 \(N\) 个节点 \(M\) 条边的无向图（无重边自环），并给出它们各自的哈密顿回路。分别判断每个图是否是平面图。

\(T\leq 100,3\leq N\leq 200,M\leq 10000\)

Solution

考虑一个带哈密顿回路的无向图，如果它是一个平面图，即可以画在平面上使得没有 \(2\) 条边需要交叉，那么哈密顿圈之外的边要么画在圈内，要么画在圈外。

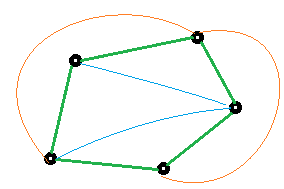（绿色的环是哈密顿圈）

如果两条边 \(e,f\) ，把它们都画在圈的内侧会相交，那么都画在外侧也一定会相交。

也就是说，对于两条边，要么没有相互约束，要么有一条约束：它们不能在圈的同侧。

求出所有边和边的约束关系，用黑白染色法判断约束关系是否为二分图。

如果是二分图，则原图是平面图。否则原图不是平面图。

似乎 \(O(M^2)\) 暴力建边不可取，但注意到的是简单极大平面图的边数 \(M\) 和节点数 \(N\) 满足关系： \[M=3N-6\]

证明：
注意到平面图欧拉定理 \(n-m+r=2\) ， \(n\) 个节点， \(m\) 条边， \(r\) 个面。
显然对于极大平面图 \(3r=2m\) ，带入得 \(m=3n-6\) 。

显然当 \(m>3n-6\) 时，这个图一定不是平面图，特判掉就好了。显然这时 \(n\) 与 \(m\) 同阶。复杂度得到了保障。

Code

//It is made by Awson on 2018.3.12
#include <bits/stdc++.h>
#define LL long long
#define dob complex<double>
#define Abs(a) ((a) < 0 ? (-(a)) : (a))
#define Max(a, b) ((a) > (b) ? (a) : (b))
#define Min(a, b) ((a) < (b) ? (a) : (b))
#define Swap(a, b) ((a) ^= (b), (b) ^= (a), (a) ^= (b))
#define writeln(x) (write(x), putchar('\n'))
#define lowbit(x) ((x)&(-(x)))
using namespace std;
const int N = 200, M = 10000;
void read(int &x) {
    char ch; bool flag = 0;
    for (ch = getchar(); !isdigit(ch) && ((flag |= (ch == '-')) || 1); ch = getchar());
    for (x = 0; isdigit(ch); x = (x<<1)+(x<<3)+ch-48, ch = getchar());
    x *= 1-2*flag;
}
void print(int x) {if (x > 9) print(x/10); putchar(x%10+48); }
void write(int x) {if (x < 0) putchar('-'); print(Abs(x)); }

int n, m, u[M+5], v[M+5], id[N+5], x;
struct tt {int to, next; }edge[(M<<5)+5];
int path[M+5], top, color[M+5];

bool dfs(int o, int col) {
    color[o] = col;
    for (int i = path[o]; i; i = edge[i].next) {
    if (color[edge[i].to] == col) return false;
    if (color[edge[i].to] == -1) if (!dfs(edge[i].to, col^1)) return false;
    }
    return true;
}
void add(int u, int v) {edge[++top].to = v, edge[top].next = path[u], path[u] = top; }
void work() {
    read(n), read(m); top = 0; memset(path, 0, sizeof(path));
    for (int i = 1; i <= m; i++) read(u[i]), read(v[i]);
    for (int i = 1; i <= n; i++) read(x), id[x] = i;
    if (m > 3*n-6) {puts("NO"); return; }
    for (int i = 1; i <= m; i++) {
    if (id[u[i]] > id[v[i]]) Swap(u[i], v[i]);
    for (int j = 1; j < i; j++)
        if ((id[u[i]] < id[u[j]] && id[v[i]] < id[v[j]] && id[u[j]] < id[v[i]]) || (id[u[j]] < id[u[i]] && id[v[j]] < id[v[i]] && id[u[i]] < id[v[j]]))
        add(i, j), add(j, i);
    }
    for (int i = 1; i <= m; i++) color[i] = -1;
    for (int i = 1; i <= m; i++)
    if (color[i] == -1) if (dfs(i, 0) == 0) {puts("NO"); return; }
    puts("YES");
}
int main() {
    int t; read(t); while (t--) work(); return 0;
}