bzoj2962 序列操作

2962: 序列操作

Time Limit: 50 Sec  Memory Limit: 256 MB
Submit: 1145  Solved: 378
[Submit][Status][Discuss]

Description

　　有一个长度为n的序列，有三个操作1.I a b c表示将[a,b]这一段区间的元素集体增加c，2.R a b表示将[a,b]区间内所有元素变成相反数，3.Q a b c表示询问[a,b]这一段区间中选择c个数相乘的所有方案的和mod 19940417的值。

Input

　　第一行两个数n，q表示序列长度和操作个数。
　　第二行n个非负整数，表示序列。
　　接下来q行每行输入一个操作I a b c或者 R a b或者Q a b c意义如题目描述。

Output

　　对于每个询问，输出选出c个数相乘的所有方案的和mod19940417的值。

Sample Input

5 5
1 2 3 4 5
I 2 3 1
Q 2 4 2
R 1 5
I 1 3 -1
Q 1 5 1

Sample Output

40
19940397
样例说明
　　做完第一个操作序列变为1 3 4 4 5。
　　第一次询问结果为3*4+3*4+4*4=40。
　　做完R操作变成-1 -3 -4 -4 -5。
　　做完I操作变为-2 -4 -5 -4 -5。
　　第二次询问结果为-2-4-5-4-5=-20。

HINT

　　100%的数据n<=50000,q<=50000,初始序列的元素的绝对值<=109，I a b c中保证[a,b]是一个合法区间，|c|<=109，R a b保证[a,b]是个合法的区间。Q a b c中保证[a,b]是个合法的区间1<=c<=min(b-a+1,20)。

Source

中国国家队清华集训 2012-2013 第三天

分析：线段树套路题.类似：传送门，这类题有一个特征就是需要维护的东西比较少：c <= 20,那么就可以开一个数组分别维护这些东西.

          f[i]表示当前区间选i个数相乘的和，显然一开始f[1] = a[pos].合并的时候f[i] = 左子树的f[i] + 右子树的f[i] + 左子树的f[j] * 右子树的f[k],j+k = i. 考虑两个修改操作对答案的影响.取反操作比较简单，注意到当i是奇数时f[i]才会变号.注意，取反以后一定要通过加上模数取模来变成正数.

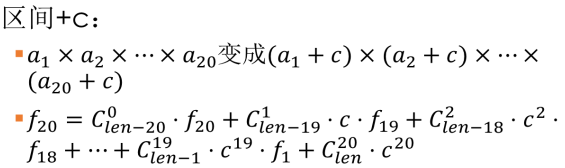          第一个操作有点鬼畜.纸上写几个例子，拆项后会再合并，就差不多能发现规律：，感性理解一下就是c的k次方，c要占k个位置，而另外的位置已经被f选的数给占了，只能在剩下的位置中选c,这大概就是组合数的意义.剩下的都可以通过合并同类项得到.

       一些细节需要注意，比如取反后一定要变成正数再来运算，f[0]一定要强制等于1,用类进行运算一定要先初始化,第一个操作对于f的处理要倒序处理,这些在之前附上链接的那道题中都有体现.

     总之，都是套路啦.

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;
const ll maxn = ,mod = ;
ll n,q;
ll a[maxn],c[maxn][];

struct node
{
    ll add,cover,f[],L,R;
    void init()
    {
        add = cover = L = R = ;
        memset(f,,sizeof(f));
        f[] = ;
    }
} e[maxn << ];

node pushup(node a,node b)
{
    node c;
    c.init();
    c.L = a.L;
    c.R = b.R;
    ll len1 = c.R - c.L + ;
    ll len2 = a.R - a.L + ;
    ll len3 = b.R - b.L + ;
    for (ll i = ; i <= min(len2,1LL * ); i++)
        for (ll j = ; j <= min(len3,1LL * ); j++)
        {
            if (i + j > )
                break;
            c.f[i + j] = (c.f[i + j] + a.f[i] * b.f[j] % mod) % mod;
        }
    c.f[] = ; //易错点
    return c;
}

void fan(ll o)
{
    ll len = e[o].R - e[o].L + ;
    for (ll i = ; i <= min(len,1LL * ); i++)
    {
        if (i %  == )
        {
            e[o].f[i] = -e[o].f[i];
            e[o].f[i] = (e[o].f[i] + mod) % mod;
        }
    }
    e[o].cover ^= ;
    e[o].add = -e[o].add;
    e[o].add = (e[o].add + mod) % mod; //取反后一定要变成正数
}

void jia(ll o,ll v)
{
    ll len = e[o].R - e[o].L + ;
    for (ll i = min(len,1LL * );i >= ; i--) //一定要倒着推
    {
        ll k = v;
        for (ll j = i - ; j >= ; j--)
        {
            e[o].f[i] = (e[o].f[i] + e[o].f[j] * c[len - j][i - j] % mod * k % mod) % mod;
            k = k * v % mod;
        }
    }
    e[o].add = (e[o].add + v) % mod;
}

void pushdown(ll o)
{
    if (e[o].cover)
    {
        fan(o * );
        fan(o *  + );
        e[o].cover = ;
    }
    if (e[o].add)
    {
        jia(o * ,e[o].add);
        jia(o *  + ,e[o].add);
        e[o].add = ;
    }
}

void build(ll o,ll l,ll r)
{
    e[o].init();
    e[o].L = l,e[o].R = r;
    if (l == r)
    {
        e[o].f[] = a[l] % mod;
        return;
    }
    ll mid = (l + r) >> ;
    build(o * ,l,mid);
    build(o *  + ,mid + ,r);
    e[o] = pushup(e[o * ],e[o *  + ]);
}

void update1(ll o,ll l,ll r,ll x,ll y,ll v)
{
    if (x <= l && r <= y)
    {
        jia(o,v);
        return;
    }
    pushdown(o);
    ll mid = (l + r) >> ;
    if (x <= mid)
        update1(o * ,l,mid,x,y,v);
    if (y > mid)
        update1(o *  + ,mid + ,r,x,y,v);
    e[o] = pushup(e[o * ],e[o *  + ]);
}

void update2(ll o,ll l,ll r,ll x,ll y)
{
    if (x <= l && r <= y)
    {
        fan(o);
        return;
    }
    pushdown(o);
    ll mid = (l + r) >> ;
    if (x <= mid)
        update2(o * ,l,mid,x,y);
    if (y > mid)
        update2(o *  + ,mid + ,r,x,y);
    e[o] = pushup(e[o * ],e[o *  + ]);
}

node query(ll o,ll l,ll r,ll x,ll y)
{
    if (x <= l && r <= y)
        return e[o];
    pushdown(o);
    ll mid = (l + r) >> ;
    if (y <= mid)
        return query(o * ,l,mid,x,y);
    else if (x > mid)
        return query(o *  + ,mid + ,r,x,y);
    else
        return pushup(query(o * ,l,mid,x,mid),query(o *  + ,mid + ,r,mid + ,y));
}

int main()
{
    scanf("%lld%lld",&n,&q);
    c[][] = ;
    for (ll i = ; i <= n; i++)
    {
        c[i][] = ;
        for (ll j = ; j <= ; j++)
            c[i][j] = (c[i - ][j] + c[i - ][j - ]) % mod;
    }
    for (ll i = ; i <= n; i++)
        scanf("%lld",&a[i]);
    build(,,n);
    while (q--)
    {
        char ch[];
        ll a,b,c;
        scanf("%s",ch);
        if (ch[] == 'I')
        {
            scanf("%lld%lld%lld",&a,&b,&c);
            update1(,,n,a,b,c);
        }
        if (ch[] == 'R')
        {
            scanf("%lld%lld",&a,&b);
            update2(,,n,a,b);
        }
        if (ch[] == 'Q')
        {
            scanf("%lld%lld%lld",&a,&b,&c);
            node temp = query(,,n,a,b);
            printf("%lld\n",temp.f[c] % mod);
        }
    }

    return ;
}