[BZOJ2144]国家集训队 跳跳棋

题目描述

跳跳棋是在一条数轴上进行的。棋子只能摆在整点上。每个点不能摆超过一个棋子。

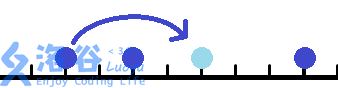
我们用跳跳棋来做一个简单的游戏：棋盘上有3颗棋子，分别在a，b，c这三个位置。我们要通过最少的跳动把他们的位置移动成x，y，z。（棋子是没有区别的）

跳动的规则很简单，任意选一颗棋子，对一颗中轴棋子跳动。跳动后两颗棋子距离不变。一次只允许跳过1颗棋子。

写一个程序，首先判断是否可以完成任务。如果可以，输出最少需要的跳动次数。

输入输出格式

输入格式：

第一行包含三个整数，表示当前棋子的位置a b c。（互不相同）

第二行包含三个整数，表示目标位置x y z。（互不相同）

输出格式：

如果无解，输出一行NO。

如果可以到达，第一行输出YES，第二行输出最少步数。

输入输出样例

输入样例#1： 复制

1 2 3
0 3 5

输出样例#1： 复制

YES
2

说明

20% 输入整数的绝对值均不超过10

40% 输入整数的绝对值均不超过10000

100% 绝对值不超过10^9

分析

这个题目是真的蛇皮，没话讲。

本题是一道LCA加二分的题目，以我的智商是看不出来的。

下面就来说一下我在SAC大佬的帮助下怎么分析的吧。

设最左边的棋子为a，中间棋子为b，最右边的棋子为c。

显而易见只有三种跳跃方式。

1.b往左边跳。

2.b往右边跳。

3.离b近的往里跳（离b远的不可以跳，因为会越过两个棋子）。

当a，c距离和b一样时，就把当前状态设为a，b，c的起始状态，而且a，b，c的起始状态只有一种。

所以判断一下a，b，c起始状态和不和x，y，z的起始状态一不一样就行了。

怎么判断呢？

显然，两个棋子往中间跳才可以回到起始状态。

但是，如果纯模拟的话就又会超时。

比如1,2,100000000。

这样就会进行很多次操作。

此时，设d1=b-a，d2=c-b。

d1小于d2时我们移动a，然后会发现d1没变，d2减小了d1所以我们可以连续走d2/d1次，反之亦然，此时d2小于d1了换个方向走。注意：d2%d1等于0时走d2/d1-1步就到根了。

然后怎么判断要走多少步呢？

枚举显然不行。

那就二分吧。

如果当前二分得到的mid可以使他们状态相同。

缩小上界，否则扩大下界，下面就贴上代码了（自认为写的很清楚）

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
void sot(ll &a,ll &b,ll &c)
{
    if(a>b)
    swap(a,b);
    if(a>c)
    swap(a,c);
    if(b>c)
    swap(b,c);
}
ll min(ll x,ll y)
{
    if(x>y)
    return y;
    return x;
}
ll getfa(ll a,ll b,ll c,ll &dep,ll &d)
{
    ll d1=b-a,d2=c-b;
    while(d1!=d2)
    {
        if(d1<d2)
        {
            ll sum=d2/d1,t=d2%d1;
            if(t==)
            {
                dep+=(sum-);
                d=d1;
                return a+(sum-)*d1;
            }
            else
            {
                dep+=sum;
                d2=t;
                a+=(sum)*d1;
                b+=(sum)*d1;

            }
        }
        else
        {
            ll sum=d1/d2,t=d1%d2;
            if(t==)
            {
                dep+=(sum-);
                d=d2;
                return a;
            }
            else
            {
                dep+=sum;
                d1=t;
                b-=(sum)*d2;
                c-=(sum)*d2;
            }
        }
    }
    dep=;
    d=d1;
    return a;
}
void fa(ll &a,ll &b,ll &c,ll step)
{
    ll d1=b-a,d2=c-b;
    while(step>)
    {
        if(d1<d2)
        {
            ll sum=d2/d1,t=d2%d1;
            if(sum>=step)
            {
                a+=step*d1;
                b+=step*d1;
                if(b==c) b=a,a-=d1;
                return;
            }
            else
            {
                step-=sum;
                b=c-t;
                a=b-d1;
                d2=t;
            }
        }
        else
        {
            ll sum=d1/d2,t=d1%d2;
            if(sum>=step)
            {
                b-=step*d2;
                c-=step*d2;
                if(a==b) b=c,c+=d2;
                return;
            }
            else
            {
                step-=sum;
                b=a+t;
                c=b+d2;
                d1=t;
            }
        }
    }
}
int main()
{
    ll a,b,c,x,y,z,dep1=,dep2=,len=,k=,kk=;
    cin>>a>>b>>c>>x>>y>>z;
    sot(a,b,c);
    sot(x,y,z);
    ll kzj=getfa(a,b,c,dep1,k);
    ll pwq=getfa(x,y,z,dep2,kk);
    if(k!=kk||kzj!=pwq) {cout<<"NO";return ;}
    else
    {
        if(dep1<dep2)
        {
            len+=dep2-dep1;
            fa(x,y,z,len);
        }
        else
        {
            len+=dep1-dep2;
            fa(a,b,c,len);
        }
    }
    ll l=,r=min(dep1,dep2),ans=;
    while(l<=r)
    {
        ll mid=(l+r)/;
        ll a1=a,b1=b,c1=c,x1=x,y1=y,z1=z;
        fa(a1,b1,c1,mid);
        fa(x1,y1,z1,mid);
        if(a1==x1&&b1==y1&&c1==z1)
        r=mid-,ans=mid;
        else
        l=mid+;
    }
    cout<<"YES"<<endl;
    cout<<ans*+len;
}