求最小生成树——Kruskal算法

给定一个带权值的无向图，要求权值之和最小的生成树，常用的算法有Kruskal算法和Prim算法。这两个算法其实都是贪心思想的使用，但又能求出最优解。（代码借鉴http://blog.csdn.net/u014488381）

一.Kruskal算法

Kruskal算法的基本思想：先将所有边按权值从小到大排序，然后按顺序选取每条边，假如一条边的两个端点不在同一个集合中，就将这两个端点合并到同一个集合中；假如两个端点在同一个集合中，说明这两个端点已经连通了，就将当前这条边舍弃掉；当所有顶点都在同一个集合时，说明最小生成树已经形成。（写代码的时候会将所有边遍历一遍）

来看一个例子：

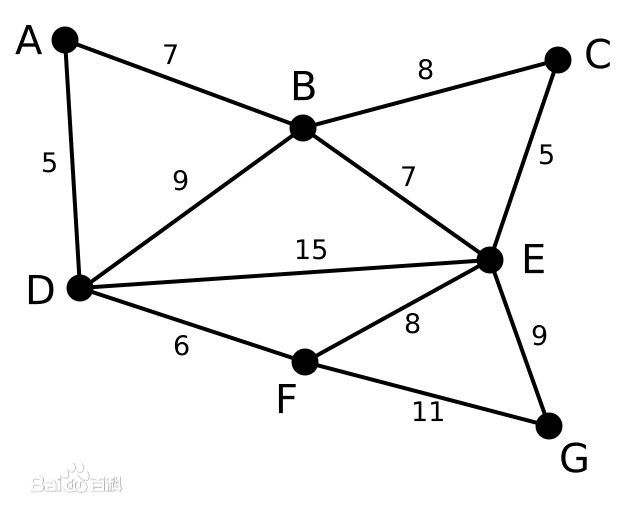
步骤：

（1）先根据权值把边排序：

AD 5

CE 5

DF 6

AB 7

BE 7

BC 8

EF 8

BD 9

EG 9

FG 11

（2）

选择AD这条边，将A、D加到同一个集合1中

选择CE这条边，将C、E加到同一个集合2中（不同于AD的集合）

选择DF这条边，由于D已经在集合1中，因此将F加入到集合1中，集合变为A、D、F

选择AB这条边，同理，集合1变为A、B、D、F

选择BE这条边，由于B在集合1中，E在集合2中，因此将两个集合合并，形成一个新的集合ABCDEF

由于E、F已经在同一集合中，舍弃掉BC这条边；同理舍弃掉EF、BD

选择EG这条边，此时所有元素都已经在同一集合中，最小生成树形成

象征性地舍弃掉FG这条边

实现代码如下：

#include <iostream>
#include <cstring>
#define MaxSize 20
using namespace std;
 
struct Edge{
    int begin;
    int end;
    int weight;
};
struct Graph{
    char ver[MaxSize + ];
    int edg[MaxSize][MaxSize];
};
 
void CreateGraph(Graph *g) {
    int VertexNum;
    char Ver;
    int i = ;
    cout << "输入图的顶点:" << endl;
    while ((Ver = getchar()) != '\n') {
        g->ver[i] = Ver;
        i++;
    }
    g->ver[i] = '\0';
    VertexNum = strlen(g->ver);
    cout << "输入相应的邻接矩阵" << endl;
    for (int i = ; i < VertexNum; i++) {
        for (int j = ; j < VertexNum; j++) {
            cin >> g->edg[i][j];    //输入0则为没有边相连啊
        }
    }
}
 
void PrintGraph(Graph g) {
    int VertexNum = strlen(g.ver);
    cout << "图的顶点为:" << endl;
    for (int i = ; i < VertexNum; i++) {
        cout << g.ver[i] << " ";
    }
    cout << endl;
    cout << "图的邻接矩阵为:" << endl;
    for (int i = ; i < VertexNum; i++) {
        for (int j = ; j < VertexNum; j++) {
            cout << g.edg[i][j] << " ";
        }
        cout << endl;
    }
}
 
int getVerNum(Graph g) {
    return strlen(g.ver);
}
 
int getEdgeNum(Graph g) {
    int res = ;
    int VertexNum = getVerNum(g);
    for (int i = ; i < VertexNum; i++) {
        //邻接矩阵对称，计算上三角元素和即可
        for (int j = i +  /*假设没有自己指向自己的*/; j < VertexNum; j++) {
            if (g.edg[i][j] != ) res++;
        }
    }
    return res;
}
 
Edge *CreateEdges(Graph g) {
    int k = ;
    int EdgeNum = getEdgeNum(g);
    int VertexNum = getVerNum(g);
    Edge * p = new Edge[EdgeNum];
    for (int i = ; i < VertexNum; i++) {
        for (int j = i; j < VertexNum; j++) {
            if (g.edg[i][j] != ) {
                p[k].begin = i;
                p[k].end = j;
                p[k].weight = g.edg[i][j];
                k++;
            }
        }
    }
    for (int i = ; i < EdgeNum - ; i++) {
        Edge minWeightEdge = p[i];
        for (int j = i + ; j < EdgeNum; j++) {
            if (minWeightEdge.weight > p[j].weight) {
                Edge temp = minWeightEdge;
                minWeightEdge = p[j];
                p[j] = temp;
            }
        }
        p[i] = minWeightEdge;
    }
    return p;
}
 
void Kruskal(Graph g) {
    int VertexNum = getVerNum(g);
    int EdgeNum = getEdgeNum(g);
    Edge *p = CreateEdges(g);
    int *index = new int[VertexNum];    //index数组，其元素为连通分量的编号，index[i]==index[j]表示编号为i和j的顶点在同一连通分量中
    int *MSTEdge = new int[VertexNum - ];    //用来存储已确定的最小生成树的**边的编号**，共VertexNum-1条边
    int k = ;
    int WeightSum = ;
    int IndexBegin, IndexEnd;
    for (int i = ; i < VertexNum; i++) {
        index[i] = -;    //初始化所有index为-1
    }
    for (int i = ; i < VertexNum - ; i++) {
        for (int j = ; j < EdgeNum; j++) {
            if ( !(index[p[j].begin] >=  && index[p[j].end] >=  && index[p[j].begin] == index[p[j].end] /*若成立表明p[j].begin和p[j].end已在同一连通块中（且可相互到达，废话）*/) ) {
                MSTEdge[i] = j;
                if (index[p[j].begin] == - && index[p[j].end] == -) {
                    index[p[j].begin] = index[p[j].end] = i;
                }
                else if (index[p[j].begin] == - && index[p[j].end] >= ) {
                    index[p[j].begin] = i;
                    IndexEnd = index[p[j].end];
                    for (int n = ; n < VertexNum; n++) {
                        if (index[n] == IndexEnd) {
                            index[n] == i;
                        }
                    }
                }
                else if (index[p[j].begin] >=  && index[p[j].end] == -) {
                    index[p[j].end] = i;
                    IndexBegin = index[p[j].begin];
                    /*将连通分量合并（或者说将没加入连通分量的顶点加进去，然后将原来连通分量的值改了）*/
                    for (int n = ; n < VertexNum; n++) {
                        if (index[n] == IndexBegin) {
                            index[n] == i;
                        }
                    }
                }
                else {
                    IndexBegin = index[p[j].begin];
                    IndexEnd = index[p[j].end];
                    for (int n = ; n < VertexNum; n++) {
                        if (index[n] == IndexBegin || index[n] == IndexEnd) {
                            index[n] = i;
                         }
                    }
                }
                break;
            }
        }
    }
    cout << "MST的边为:" << endl;
    for (int i = ; i < VertexNum - ; i++) {
        cout << g.ver[p[MSTEdge[i]].begin] << "--" << g.ver[p[MSTEdge[i]].end] << endl;
        WeightSum += p[MSTEdge[i]].weight;
    }
    cout << "MST的权值为:" << WeightSum << endl;
}

二.Prim算法（代码还没理解）

Prim算法的基本思想：设置两个存放顶点的集合，第一个集合初始化为空，第二个集合初始化为一个包含所有顶点的集合。首先把图中的任意一个顶点a放进第一个集合，然后在第二个集合中找到一个顶点b，使b到第一个集合中的任意一点的权值最小，然后把b从第二个集合移到第一个集合。接着在第二个集合中找到顶点c，使c到a或b的权值比到第二个集合中的其他任何顶点到a或b的权值都要小，然后把c从第二个集合移到第一个集合中。以此类推，当第二个集合中的顶点全部移到第一个集合时，最小生成树产生。

以上面的图再次作为例子：

设第一个集合为V，第二个集合为U。

V={A}, U={B, C, D, E, F, G}

（1）A连接了两个顶点，B和D，AB权值为7，AD权值为5，选择权值小的一条边和相应的顶点D，将D加入集合V中。V={A, D}, U={B, C, E, F, G}

（2）观察包含V中的元素A和D的边，AB权值为7，BD权值为9，DE权值为15，DF权值为6，将F加入V中。V={A, D, F}, U={B, C, E, G}

（3）依次将B(AB)、E(BE)、C(CE)、G(EG)加入到集合V中。

（4）最小生成树的边包括：AD DF AB BE CE EG，problem solved

实现代码如下：

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
#define MaxSize 20
struct Graph{
    char ver[MaxSize + ];
    int edg[MaxSize][MaxSize];
};
 
void CreateGraph(Graph *g) {
    int VertexNum;
    char Ver;
    int i = ;
    cout << "输入图的顶点:" << endl;
    while ((Ver = getchar()) != '\n') {
        g->ver[i] = Ver;
        i++;
    }
    g->ver[i] = '\0';
    VertexNum = strlen(g->ver);
    cout << "输入相应的邻接矩阵" << endl;
    for (int i = ; i < VertexNum; i++) {
        for (int j = ; j < VertexNum; j++) {
            cin >> g->edg[i][j];    //输入0则为没有边相连啊
        }
    }
}
 
void PrintGraph(Graph g) {
    int VertexNum = strlen(g.ver);
    cout << "图的顶点为:" << endl;
    for (int i = ; i < VertexNum; i++) {
        cout << g.ver[i] << " ";
    }
    cout << endl;
    cout << "图的邻接矩阵为:" << endl;
    for (int i = ; i < VertexNum; i++) {
        for (int j = ; j < VertexNum; j++) {
            cout << g.edg[i][j] << " ";
        }
        cout << endl;
    }
}
 
int getVerNum(Graph g) {
    return strlen(g.ver);
}
 
//将不邻接的顶点之间的权值设为
void SetWeight(Graph *g) {
    for (int i = ; i < getVerNum(*g); i++) {
        for (int j = ; j < getVerNum(*g); j++) {
            if (g->edg[i][j] == ) {
                g->edg[i][j] = INT_MAX;
            }
        }
    }
}
 
void Prim(Graph g, int *parent) {
    //V为所有顶点的集合，U为最小生成树的节点集合
    int lowcost[MaxSize];    //lowcost[k]保存着编号为k的顶点到U中所有顶点的最小权值
    int closest[MaxSize];    //closest[k]保存着U到V-U中编号为k的顶点权值最小的顶点的编号
    int used[MaxSize];
    int min;
    int VertexNum = getVerNum(g);
    for (int i = ; i < VertexNum; i++) {
        lowcost[i] = g.edg[][i];
        closest[i] = ;
        used[i] = ;
        parent[i] = -;
     }
     used[] = ;
     for (int i = ; i < VertexNum - ; i++) {
         int j = ;
         min = INT_MAX;
         for (int k = ; k < VertexNum; k++) {    //找到V-U中的与U中顶点组成的最小权值的边的顶点编号
             if (used[k] ==  && lowcost[k] < min) {
                 min = lowcost[k];
                 j = k;
             }
         }
         parent[j] = closest[j];
         used[j] = ;
         for (int k = ; k < VertexNum; k++) {   //由于j顶点加入U中，更新lowcost和closest数组中的元素，检测V-U中的顶点到j顶点的权值是否比j加入U之前的lowcost数组的元素小
             if (used[k] ==  && g.edg[j][k] < lowcost[k]) {
                 lowcost[k] = g.edg[j][k];
                 closest[k] = j;
             }
         }
     }
}
 
void PrintMST(Graph g, int *parent) {
    int VertexNum = getVerNum(g);
    int weight = ;
    cout << "MST的边为:" << endl;
    for (int i = ; i < VertexNum; i++) {
        cout << g.ver[parent[i]] << "--" << g.ver[i] << endl;
        weight += g.edg[parent[i]][i];
    }
    cout << "MST的权值为" << weight << endl;
}
 
int main() {
    Graph g;
    int parent[];
    CreateGraph(&g);
    PrintGraph(g);
    SetWeight(&g);
    Prim(g, parent);
    PrintMST(g, parent);
    return ;
}

三.Kruskal算法和Prim算法的适用情况

Kruskal算法适用于边稀疏的情况（要进行排序），Prim算法适用于边稠密的情况。