「Vijos 1284」「OIBH杯NOIP2006第二次模拟赛」佳佳的魔法阵

佳佳的魔法阵

背景

也许是为了捕捉猎物（捕捉MM？），也许是因为其它原因，总之，佳佳准备设计一个魔法阵。而设计魔法阵涉及到的最关键问题，似乎就是那些带有魔力的宝石的摆放……

描述

魔法阵是一个\(n \times m\)的格子（高n，宽m），\(n \times m\)为偶数。佳佳手中有\(n \times m\)个宝石（以\(1 \to n \times m\)编号）。佳佳从最右上角的格子开始走，从一个格子可以走到上、下、左、右4个相邻的格子，但不能走出边界。每个格子必须且仅能到过1次，这样佳佳一共走了\(n \times m\)个格子停止（随便停哪里）。佳佳每进入一个格子，就在该格子里放入一颗宝石。他是按顺序放的，也就是说——第i个进入的格子放入i号宝石。

如果两颗宝石的编号对\(\frac{n \times m}{2}\)取模的值相同，则认为这两颗宝石相互之间有微妙的影响。也就是说，我们按照宝石的编号对取\(\frac{n \times m}{2}\)模的值，将宝石分成\(\frac{n \times m}{2}\)对，其中每对都恰有两颗宝石。对于每一对宝石，设第一颗宝石在第a行第b列，另一颗宝石在第c行第d列，那么定义这2个宝石的魔力影响值为 $ k_1\times \left| a-c \right|+k_2 \times \left| b-d \right| $。

需要你求出的是，在所有合乎题意的宝石摆放方案中，所有成对的宝石间的最大魔力影响值的最小值为多少。换句话说，如果我们定义对\(\frac{n \times m}{2}\)取模的值为i的一对宝石的魔力影响值为\(a_i\)。你需要求出的就是\(\max{(a_i|i=0,1,2...)}\)的最小值。

输入格式

只有一行用空格隔开的4个整数，分别是\(n、m、k_1、k_2，n \times m \le 50，0<k_1,k_2 \le 32767\)。

输出格式

只需输出一个整数，即题目所要求的“所有成对的宝石间的最大魔力影响值的最小值”。

样例输入1

2 2 2 2

样例输出1

4

限制

1秒

---

思路

这是一道搜索+剪枝题。一看到数据范围(\(n \times m \le 50\))我便兴奋的飞起——暴搜！！！

然而没打完代码模拟赛就结束了。。。。。。

这道题的搜索的方式要一分为二(其实还是有很多重叠部分的)，前 $ \frac{n \times m}{2}$ 一部分，剩下的一部分。

注意两个剪枝

1. 最优化剪枝：很简单，当前最大值比ans大或者等于ans时直接return。
2. 可行性剪枝：接下来仔细讲讲这个吧。

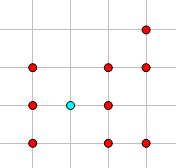
蓝色的点表示当前位置，红色的点表示访问过的位置。这种情况(左、右两点不能再访问而上下两点未访问)是一种不可行的情况。

为什么呢？

仔细想一想就能明白了。

以上述情况为例，蓝色点的上方或下方必定会构成死胡同。

像这样：

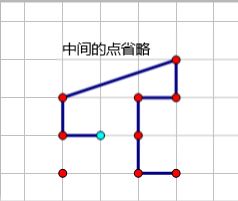
具体自己再理解理解吧。

然后上代码！

代码

#include<bits/stdc++.h>
using namespace std;
#define MAXN 55

int n, m, k1, k2, ans(0x7f7f7f7f), nn;
int a[MAXN][2];
bool vis[MAXN][MAXN];
int dir[][2] = { 1, 0, 0, 1, -1, 0, 0, -1 };

bool check( int x, int y ){
    if ( vis[x + 1][y] && vis[x - 1][y] && !vis[x][y + 1] && !vis[x][y - 1] ) return 0;
    if ( vis[x][y + 1] && vis[x][y - 1] && !vis[x + 1][y] && !vis[x - 1][y] ) return 0;
    return !vis[x][y];
} 

inline int ABS( int x ){
    return x < 0 ? -x : x;
}

inline int Get( int x, int y, int a, int b ){
    return k1 * ABS( x - a ) + k2 * ABS( y - b );
} 

void DFS( int x, int y, int wh, int cur ){
    if ( wh <= nn ) a[wh][0] = x, a[wh][1] = y;
    else cur = max( cur, Get( x, y, a[wh - nn][0], a[wh - nn][1] ) );

    if ( wh >= n * m ){
        ans = min( ans, cur );
        return;
    }
    if ( cur >= ans ) return;

    vis[x][y] = 1;
    for ( int i = 0; i < 4; ++i ){
        int tx( x + dir[i][0] ), ty( y + dir[i][1] );
        if ( !check( tx, ty ) ) continue;
        DFS( tx, ty, wh + 1, cur );
    }
    vis[x][y] = 0;
}

int main(){
    scanf( "%d%d%d%d", &n, &m, &k1, &k2 );
    for ( int i = 0; i <= n + 1; ++i ) vis[i][0] = vis[i][m + 1] = 1;
    for ( int i = 0; i <= m + 1; ++i ) vis[0][i] = vis[n + 1][i] = 1;
    nn = n * m >> 1;
    DFS( 1, m, 1, 0 );
    printf( "%d\n", ans );
    return 0;
}

秀一把 \(\LaTeX\) hahaha