文字描述

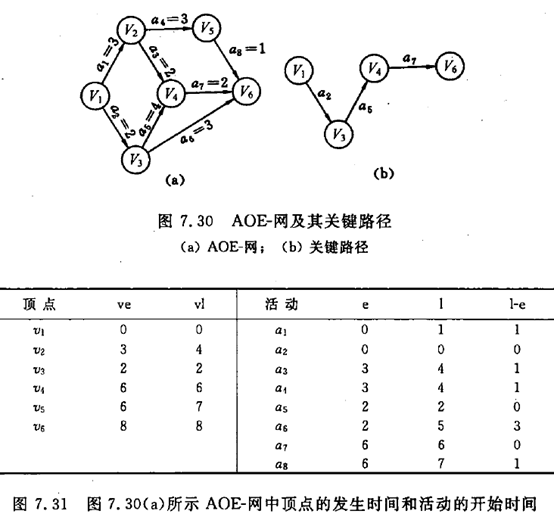
　　与AOV-网相对应的是AOE-网(Activity on Edge)即边表示活动的网。AOE-网是一个带权的有向无环图。其中，顶点表示事件Event，弧表示活动，权表示活动持续的时间。通常，AOE-网可用来估算工程的完成时间。

　　对AOE-网来说，研究的问题有两个：(1)完成整项工程至少需要多少时间？(2)哪些活动是影响工程进度的关键?　　

　　由于在AOE-网中有些活动可以并行地进行，所以完成工程的最短时间是从开始点到完成点的最长路径的长度(指路径上各活动持续时间之和，不是路径上弧的数目)。路径长度最长的路径叫做关键路径。

　　假设开始点是v1，从v1到vi的最长路径叫事件vi的最早发生时间。这个时间决定了所有以vi为尾的弧所表示的活动的最早开始时间。用e(i)表示活动ai的最早开始时间。用l(i)表示ai的最迟开始时间，这是在不推迟整个工程完成的前提下，活动ai最迟必须开始进行的时间。两者之差l(i)-e(i)表示活动ai的时间余量。我们把l(i)==e(i)的活动叫做关键活动。

　　显然，关键路径上的所有活动都是关键活动，因此提前完成非关键活动并不能加快工程的进度。

　　那么如何求得各个活动的最早开始时间e(i)和最晚开始时间l(i)呢？首先应求得事件的最早发生时间ve(j)和最迟发生时间vl(j)。如果活动ai由弧<j,k>表示，其持续时间记为dut(<j,k>)，则有如下关系：

　　e(i) = ve(j)

　　l(i) = vl(k) – dut(<j,k>)

　　求ve(j)和vl(j)需分两步进行：

　　　　(1)   从ve(0)=0开始向前递推

　　　　

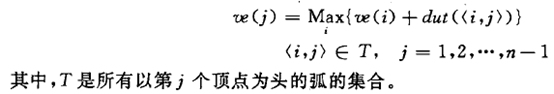
　　　　(2)   从vl(n-1)=ve(n-1)起向后递推

　　　　

　　　　这两个递推公式可以利用之前的拓扑排序算法求得。

示意图

算法分析

　　算法复杂度同拓扑排序算法，为O(n+e)。

代码实现

  1.  //
  2.  // Created by lady on 18-12-29.
  3.  //
  4.  
  5.  #include <stdlib.h>
  6.  #include <stdio.h>
  7.  #define MAX_VERTEX_NUM 20 //最大顶点数
  8.  #define MAX_EDGE_NUM 50 //最大弧数
  9.  typedef enum {DG,DN, UDG, UDN} GraphKind; //{有向图，有向网，无向图，无向网}
  10.  typedef struct ArcNode{
  11.      int adjvex;    //该弧所指向的顶点的位置
  12.      struct ArcNode *nextarc;    //指向下一条弧的指针
  13.      int info;    //该弧相关信息的指针
  14.  }ArcNode;
  15.  typedef struct VNode{
  16.      char data[];//顶点信息
  17.      ArcNode *firstarcIN;//第一条以该顶点为弧头的弧结点，其他顶点->该结点
  18.      ArcNode *firstarcOUT;//第一条以该顶点为弧尾的弧结点，该结点->其他顶点
  19.  }VNode, AdjList[MAX_VERTEX_NUM];
  20.  typedef struct{
  21.      AdjList vertices;
  22.      int vexnum;//图的顶点数
  23.      int arcnum;//图的弧数
  24.      int kind; //图的种类标志
  25.  }ALGraph;
  26.  
  27.  //根据顶点信息，返回该顶点在图中的位置坐标。
  28.  int LocateVex(ALGraph *G, char data[])
  29.  {
  30.      int i = ;
  31.      for(i=; i<G->vexnum; i++){
  32.          if(!strncmp(G->vertices[i].data, data, strlen(G->vertices[i].data))){
  33.              return i;
  34.          }
  35.      }
  36.      return -;
  37.  }
  38.  
  39.  //利用头插法，在弧结点链表头部，插入位置v的弧结点
  40.  int InsFirst(ArcNode *L, int v, int weight)
  41.  {
  42.      if((L==NULL) || (v<)){
  43.          return -;
  44.      }
  45.      ArcNode *n = (ArcNode *)malloc(sizeof(struct ArcNode));
  46.      n->adjvex = v;
  47.      n->nextarc = L->nextarc;
  48.      n->info = weight;
  49.      L->nextarc = n;
  50.      return ;
  51.  }
  52.  
  53.  //采用邻接表存储方法，创建有向网，即带权的有向图
  54.  int CreateDN(ALGraph *G)
  55.  {
  56.      printf("开始创建一个有向图,请输入顶点数，弧数:");
  57.      int i = , j = , k = ;
  58.      char v1[] = {}, v2[]={}, info[] = {};
  59.      char tmp[] = {};
  60.      G->kind = DN;
  61.      scanf("%d,%d", &G->vexnum, &G->arcnum);
  62.      for(i=; i<G->vexnum; i++){
  63.          printf("输入第%d个顶点: ", i+);
  64.          memset(G->vertices[i].data, , sizeof(G->vertices[i].data));
  65.          scanf("%s", G->vertices[i].data);
  66.          G->vertices[i].firstarcOUT = (struct ArcNode *)malloc(sizeof(struct ArcNode));
  67.          G->vertices[i].firstarcOUT->adjvex = -;
  68.          G->vertices[i].firstarcOUT->nextarc = NULL;
  69.          G->vertices[i].firstarcIN = (struct ArcNode *)malloc(sizeof(struct ArcNode));
  70.          G->vertices[i].firstarcIN->adjvex = -;
  71.          G->vertices[i].firstarcIN->nextarc = NULL;
  72.      }
  73.      for(k=; k<G->arcnum; k++)
  74.      {
  75.          printf("输入第%d条弧(顶点1, 顶点2, 权值): ", k+);
  76.          memset(tmp, , sizeof(tmp));
  77.          scanf("%s", tmp);
  78.  //      sscanf(tmp, "%[^','],%s[^\\n]", v1, v2);
  79.          sscanf(tmp, "%[^','],%[^','],%s[^\\n]", v1, v2, info);
  80.          i = LocateVex(G, v1);
  81.          j = LocateVex(G, v2);
  82.          if(i< || j<){
  83.              printf("<%s,%s> is a invalid arch!\n", v1, v2);
  84.              return -;
  85.          }
  86.          InsFirst(G->vertices[i].firstarcOUT, j, atoi((const char *)info));
  87.          InsFirst(G->vertices[j].firstarcIN, i, atoi((const char *)info));
  88.      }
  89.      return ;
  90.  }
  91.  
  92.  void printG(ALGraph *G)
  93.  {
  94.      printf("\n");
  95.      if(G->kind == DG){
  96.          printf("类型：有向图；顶点数 %d, 弧数 %d\n", G->vexnum, G->arcnum);
  97.      }else if(G->kind == DN){
  98.          printf("类型：有向网；顶点数 %d, 弧数 %d\n", G->vexnum, G->arcnum);
  99.      }else if(G->kind == UDG){
  100.          printf("类型：无向图；顶点数 %d, 弧数 %d\n", G->vexnum, G->arcnum);
  101.      }else if(G->kind == UDN){
  102.          printf("类型：无向网；顶点数 %d, 弧数 %d\n", G->vexnum, G->arcnum);
  103.      }
  104.      int i = ;
  105.      ArcNode *p = NULL;
  106.      printf("邻接表:\n");
  107.      for(i=; i<G->vexnum; i++){
  108.          printf("(%d,%s)\t", i,G->vertices[i].data);
  109.          p = G->vertices[i].firstarcOUT;
  110.          while(p){
  111.              if(p->adjvex >= )
  112.                  printf("(%d,%s) %d\t", p->adjvex, G->vertices[p->adjvex].data, p->info);
  113.              p = p->nextarc;
  114.          }
  115.          printf("\n");
  116.      }
  117.      printf("逆邻接表:\n");
  118.      for(i=; i<G->vexnum; i++){
  119.          printf("(%d,%s)\t", i,G->vertices[i].data);
  120.          p = G->vertices[i].firstarcIN;
  121.          while(p){
  122.              if(p->adjvex >= )
  123.                  printf("(%d,%s) %d\t", p->adjvex, G->vertices[p->adjvex].data, p->info);
  124.              p = p->nextarc;
  125.          }
  126.          printf("\n");
  127.      }
  128.      return;
  129.  }
  130.  
  131.  #define STACK_INIT_SIZE 20  //栈的初始分配量大小
  132.  #define STACK_INCREMENT 5   //栈容量不足时需新增的容量大小
  133.  typedef struct {
  134.      int *base;  //指向栈底指针
  135.      int *top;   //指向栈顶指针
  136.      int stacksize;  //栈的当前容量大小
  137.  }SqStack;
  138.  int InitStack(SqStack *s);  //初始化一个栈
  139.  int StackEmpty(SqStack *s); //判断栈是否为空
  140.  int Push(SqStack *S, int *e);  //入栈函数
  141.  int Pop(SqStack *S, int *e);    //出栈函数
  142.  
  143.  //算法各个顶点的入度，并将结果存放在indegree数组中
  144.  int FindInDegree(ALGraph *G, int indegree[])
  145.  {
  146.      printf("\n对各个顶点求入度...\n");
  147.      int i = ;
  148.      ArcNode *p = NULL;
  149.      for(i=; i<G->vexnum; i++) {
  150.          p = G->vertices[i].firstarcIN;
  151.          while (p) {
  152.              if (p->adjvex >= ) {
  153.                  indegree[i] += ;
  154.              }
  155.              p = p->nextarc;
  156.          }
  157.      }
  158.      for(i=; i<G->vexnum; i++){
  159.          printf("(%d,%s)的入度为%d\n", i, G->vertices[i].data, indegree[i]);
  160.      }
  161.      return ;
  162.  }
  163.  int ve[MAX_EDGE_NUM] = {};
  164.  int vl[MAX_EDGE_NUM] = {};
  165.  
  166.  int ToplogicalSort(ALGraph *G, SqStack *T)
  167.  {
  168.      int i = ;
  169.      int j = ;
  170.      int k = ;
  171.      int count = ;
  172.      int indegree[MAX_VERTEX_NUM] = {};
  173.      ArcNode *p = NULL;
  174.      SqStack S;
  175.      //求各个顶点的入度
  176.      FindInDegree(G, indegree);
  177.      //初始化栈S，保存零入度顶点栈
  178.      InitStack(&S);
  179.      //将入度为0的顶点入栈S.
  180.      for(i=; i<G->vexnum; i++){
  181.          if(!indegree[i]) {
  182.              Push(&S, &i);
  183.          }
  184.      }
  185.      //初始化栈T，为拓扑序列顶点栈
  186.      InitStack(T);
  187.      //初始化
  188.      for(i=; i<G->vexnum; i++){
  189.          ve[i] = ;
  190.      }
  191.      printf("\n进行拓扑排序:");
  192.      while(StackEmpty(&S)){
  193.          Pop(&S, &j);
  194.          //j号顶点入T栈并计数
  195.          Push(T, &j);
  196.          ++count;
  197.          printf("(%d,%s)\t", j, G->vertices[j].data);
  198.          //对j号顶点的每个邻接点的入度减1
  199.          for(p=G->vertices[j].firstarcOUT; p; p=p->nextarc){
  200.              k = p->adjvex;
  201.              if(k<){
  202.                  continue;
  203.              }
  204.              //若入度为0,则入栈S
  205.              if(!(--indegree[k])){
  206.                  Push(&S, &k);
  207.              }
  208.              if(ve[j]+p->info > ve[k])
  209.                  ve[k] = ve[j]+p->info;
  210.          }
  211.      }
  212.      printf("\n");
  213.      if(count<G->vexnum){
  214.          //该有向网有环
  215.          return -;
  216.      }else{
  217.          return ;
  218.      }
  219.  }
  220.  
  221.  //G为有向图， 输出G的各项关键活动
  222.  int CriticalPath(ALGraph *G)
  223.  {
  224.      SqStack T;
  225.      if(ToplogicalSort(G, &T)<){
  226.          return -;
  227.      }
  228.      int i = ;
  229.      int j = ;
  230.      int k = ;
  231.      int dut = ;
  232.      ArcNode *p = NULL;
  233.      //初始化顶点时间的最迟发生时间
  234.      for(i=; i<G->vexnum; i++){
  235.          vl[i] = ve[i];
  236.      }
  237.      //按照拓扑逆序求各顶点的vl值
  238.      while(StackEmpty(&T)){
  239.          Pop(&T, &j);
  240.  
  241.          for(p=G->vertices[j].firstarcOUT; p; p=p->nextarc){
  242.              k = p->adjvex;
  243.              if(k<)
  244.                  continue;
  245.              dut = p->info; //dut(<j,k>)
  246.              if(vl[k]-dut < vl[j])
  247.                  vl[j] = vl[k] - dut;
  248.          }
  249.  
  250.          for(p=G->vertices[j].firstarcIN; p; p=p->nextarc) {
  251.              k = p->adjvex;
  252.              if (k < )
  253.                  continue;
  254.              dut = p->info; //dut<k,j>
  255.  
  256.              if (vl[j] - dut > vl[k]) {
  257.                  vl[k] = vl[j] - dut;
  258.              }
  259.          }
  260.      }
  261.      printf("\n输出各个顶点的最早发生时间ve和最晚发生时间vl\n");
  262.      for(i=; i<G->vexnum; i++){
  263.          printf("ve(%d,%s)=%d\t", i, G->vertices[i].data, ve[i]);
  264.          printf("vl(%d,%s)=%d\n", i, G->vertices[i].data, vl[i]);
  265.      }
  266.      int ee = ;
  267.      int el = ;
  268.      char tag = ;
  269.      printf("\n输出各活动的最早发生时间ee和最晚发生时间el, *表示该活动为关键路径\n");
  270.      for(j=; j<G->vexnum; j++){
  271.          for(p=G->vertices[j].firstarcOUT; p; p=p->nextarc){
  272.              k = p->adjvex;
  273.              if(k<){
  274.                  continue;
  275.              }
  276.              dut = p->info;
  277.              ee = ve[j];
  278.              el = vl[k]-dut;
  279.              tag = (ee==el)?'*':' ';
  280.              //输出关键活动
  281.              printf("(%d,%s)->(%d,%s), weight:%d, ee=%d, el=%d, tag=%c\n", j, G->vertices[j].data, k, G->vertices[k].data, dut, ee, el, tag);
  282.          }
  283.      }
  284.      return ;
  285.  }
  286.  
  287.  int main(int argc, char *argv[])
  288.  {
  289.      ALGraph G;
  290.      //创建有向图
  291.      if(CreateDN(&G)<){
  292.          printf("创建有向图时出错!\n");
  293.          return -;
  294.      }
  295.      //打印图
  296.      printG(&G);
  297.      //求关键路径
  298.      CriticalPath(&G);
  299.      return ;
  300.  }
  301.  
  302.  int InitStack(SqStack *S){
  303.      S->base = (int *) malloc(STACK_INIT_SIZE * sizeof(int));
  304.      if(!S->base){
  305.          return -;
  306.      }
  307.      S->top = S->base;
  308.      S->stacksize = STACK_INIT_SIZE;
  309.      return ;
  310.  }
  311.  
  312.  int StackEmpty(SqStack *s){
  313.      if(s->base == s->top){
  314.          return ;
  315.      }else{
  316.          return -;
  317.      }
  318.  }
  319.  
  320.  int Push(SqStack *s, int *e){
  321.      if((s->top-s->base) >= s->stacksize){
  322.          s->base = (int*)realloc(s->base, (s->stacksize+STACK_INCREMENT)*(sizeof(int)));
  323.          if(!s->base){
  324.              return -;
  325.          }
  326.          s->top = s->base + s->stacksize;
  327.          s->stacksize += STACK_INCREMENT;
  328.      }
  329.      if(e == NULL){
  330.          return -;
  331.      }else{
  332.          *s->top = *e;
  333.      }
  334.      s->top += ;
  335.      return ;
  336.  }
  337.  
  338.  int Pop(SqStack *s, int *e)
  339.  {
  340.      if(s->top == s->base) {
  341.          return -;
  342.      }else{
  343.          s->top -=;
  344.          *e = *s->top;
  345.          return ;
  346.      }
  347.  }

求有向无环网的关键路径

代码运行

  1. /home/lady/CLionProjects/untitled/cmake-build-debug/untitled
    开始创建一个有向图,请输入顶点数，弧数:9,11
    输入第1个顶点: V1
    输入第2个顶点: V2
    输入第3个顶点: V3
    输入第4个顶点: V4
    输入第5个顶点: V5
    输入第6个顶点: V6
    输入第7个顶点: V7
    输入第8个顶点: V8
    输入第9个顶点: V9
    输入第1条弧(顶点1, 顶点2, 权值): V1,V2,6
    输入第2条弧(顶点1, 顶点2, 权值): V1,V3,4
    输入第3条弧(顶点1, 顶点2, 权值): V1,V4,5
    输入第4条弧(顶点1, 顶点2, 权值): V2,V5,1
    输入第5条弧(顶点1, 顶点2, 权值): V3,V5,1
    输入第6条弧(顶点1, 顶点2, 权值): V4,V6,2
    输入第7条弧(顶点1, 顶点2, 权值): V5,V7,9
    输入第8条弧(顶点1, 顶点2, 权值): V5,V8,7
    输入第9条弧(顶点1, 顶点2, 权值): V6,V8,4
    输入第10条弧(顶点1, 顶点2, 权值): V7,V9,2
    输入第11条弧(顶点1, 顶点2, 权值): V8,V9,4
  2.  
  3. 类型：有向网；顶点数 9, 弧数 11
    邻接表:
    (0,V1)    (3,V4) 5    (2,V3) 4    (1,V2) 6    
    (1,V2)    (4,V5) 1    
    (2,V3)    (4,V5) 1    
    (3,V4)    (5,V6) 2    
    (4,V5)    (7,V8) 7    (6,V7) 9    
    (5,V6)    (7,V8) 4    
    (6,V7)    (8,V9) 2    
    (7,V8)    (8,V9) 4    
    (8,V9)    
    逆邻接表:
    (0,V1)    
    (1,V2)    (0,V1) 6    
    (2,V3)    (0,V1) 4    
    (3,V4)    (0,V1) 5    
    (4,V5)    (2,V3) 1    (1,V2) 1    
    (5,V6)    (3,V4) 2    
    (6,V7)    (4,V5) 9    
    (7,V8)    (5,V6) 4    (4,V5) 7    
    (8,V9)    (7,V8) 4    (6,V7) 2    
  4.  
  5. 对各个顶点求入度...
    (0,V1)的入度为0
    (1,V2)的入度为1
    (2,V3)的入度为1
    (3,V4)的入度为1
    (4,V5)的入度为2
    (5,V6)的入度为1
    (6,V7)的入度为1
    (7,V8)的入度为2
    (8,V9)的入度为2
  6.  
  7. 进行拓扑排序:(0,V1)    (1,V2)    (2,V3)    (4,V5)    (6,V7)    (3,V4)    (5,V6)    (7,V8)    (8,V9)    
  8.  
  9. 输出各个顶点的最早发生时间ve和最晚发生时间vl
    ve(0,V1)=0    vl(0,V1)=0
    ve(1,V2)=6    vl(1,V2)=6
    ve(2,V3)=4    vl(2,V3)=6
    ve(3,V4)=5    vl(3,V4)=8
    ve(4,V5)=7    vl(4,V5)=7
    ve(5,V6)=7    vl(5,V6)=10
    ve(6,V7)=16    vl(6,V7)=16
    ve(7,V8)=14    vl(7,V8)=14
    ve(8,V9)=18    vl(8,V9)=18
  10.  
  11. 输出各活动的最早发生时间ee和最晚发生时间el, *表示该活动为关键路径
    (0,V1)->(3,V4), weight:5, ee=0, el=3, tag= 
    (0,V1)->(2,V3), weight:4, ee=0, el=2, tag= 
    (0,V1)->(1,V2), weight:6, ee=0, el=0, tag=*
    (1,V2)->(4,V5), weight:1, ee=6, el=6, tag=*
    (2,V3)->(4,V5), weight:1, ee=4, el=6, tag= 
    (3,V4)->(5,V6), weight:2, ee=5, el=8, tag= 
    (4,V5)->(7,V8), weight:7, ee=7, el=7, tag=*
    (4,V5)->(6,V7), weight:9, ee=7, el=7, tag=*
    (5,V6)->(7,V8), weight:4, ee=7, el=10, tag= 
    (6,V7)->(8,V9), weight:2, ee=16, el=16, tag=*
    (7,V8)->(8,V9), weight:4, ee=14, el=14, tag=*
  12.  
  13. Process finished with exit code 0
  1. /home/lady/CLionProjects/untitled/cmake-build-debug/untitled
    开始创建一个有向图,请输入顶点数，弧数:6,8
    输入第1个顶点: V1
    输入第2个顶点: V2
    输入第3个顶点: V3
    输入第4个顶点: V4
    输入第5个顶点: V5
    输入第6个顶点: V6
    输入第1条弧(顶点1, 顶点2, 权值): V1,V2,3
    输入第2条弧(顶点1, 顶点2, 权值): V1,V3,2
    输入第3条弧(顶点1, 顶点2, 权值): V2,V4,2
    输入第4条弧(顶点1, 顶点2, 权值): V2,V5,3
    输入第5条弧(顶点1, 顶点2, 权值): V3,V4,4
    输入第6条弧(顶点1, 顶点2, 权值): V3,V6,3
    输入第7条弧(顶点1, 顶点2, 权值): V4,V6,2
    输入第8条弧(顶点1, 顶点2, 权值): V5,V6,1
  2.  
  3. 类型：有向网；顶点数 6, 弧数 8
    邻接表:
    (0,V1)    (2,V3) 2    (1,V2) 3    
    (1,V2)    (4,V5) 3    (3,V4) 2    
    (2,V3)    (5,V6) 3    (3,V4) 4    
    (3,V4)    (5,V6) 2    
    (4,V5)    (5,V6) 1    
    (5,V6)    
    逆邻接表:
    (0,V1)    
    (1,V2)    (0,V1) 3    
    (2,V3)    (0,V1) 2    
    (3,V4)    (2,V3) 4    (1,V2) 2    
    (4,V5)    (1,V2) 3    
    (5,V6)    (4,V5) 1    (3,V4) 2    (2,V3) 3    
  4.  
  5. 对各个顶点求入度...
    (0,V1)的入度为0
    (1,V2)的入度为1
    (2,V3)的入度为1
    (3,V4)的入度为2
    (4,V5)的入度为1
    (5,V6)的入度为3
  6.  
  7. 进行拓扑排序:(0,V1)    (1,V2)    (4,V5)    (2,V3)    (3,V4)    (5,V6)    
  8.  
  9. 输出各个顶点的最早发生时间ve和最晚发生时间vl
    ve(0,V1)=0    vl(0,V1)=0
    ve(1,V2)=3    vl(1,V2)=4
    ve(2,V3)=2    vl(2,V3)=2
    ve(3,V4)=6    vl(3,V4)=6
    ve(4,V5)=6    vl(4,V5)=7
    ve(5,V6)=8    vl(5,V6)=8
  10.  
  11. 输出各活动的最早发生时间ee和最晚发生时间el, *表示该活动为关键路径
    (0,V1)->(2,V3), weight:2, ee=0, el=0, tag=*
    (0,V1)->(1,V2), weight:3, ee=0, el=1, tag= 
    (1,V2)->(4,V5), weight:3, ee=3, el=4, tag= 
    (1,V2)->(3,V4), weight:2, ee=3, el=4, tag= 
    (2,V3)->(5,V6), weight:3, ee=2, el=5, tag= 
    (2,V3)->(3,V4), weight:4, ee=2, el=2, tag=*
    (3,V4)->(5,V6), weight:2, ee=6, el=6, tag=*
    (4,V5)->(5,V6), weight:1, ee=6, el=7, tag= 
  12.  
  13. Process finished with exit code 0

图->有向无环图->求关键路径的更多相关文章

  1. 图->有向无环图->拓扑排序

    文字描述 关于有向无环图的基础定义: 一个无环的有向图称为有向无环图,简称DAG图(directed acycline graph).DAG图是一类较有向树更一般的特殊有向图. 举个例子说明有向无环图 ...

  2. 有向无环图的应用—AOV网 和 拓扑排序

    有向无环图:无环的有向图,简称 DAG (Directed Acycline Graph) 图. 一个有向图的生成树是一个有向树,一个非连通有向图的若干强连通分量生成若干有向树,这些有向数形成生成森林 ...

  3. 【拓扑】【宽搜】CSU 1084 有向无环图 (2016湖南省第十二届大学生计算机程序设计竞赛)

    题目链接: http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1804 题目大意: 一个有向无环图(DAG),有N个点M条有向边(N,M<=105 ...

  4. Expm 4_2 有向无环图中的最短路径问题

    [问题描述] 建立一个从源点S到终点E的有向无环图,设计一个动态规划算法求出从S到E的最短路径值,并输出相应的最短路径. 解: package org.xiu68.exp.exp4; import j ...

  5. 网络流24题 第三题 - CodeVS1904 洛谷2764 最小路径覆盖问题 有向无环图最小路径覆盖 最大流 二分图匹配 匈牙利算法

    欢迎访问~原文出处——博客园-zhouzhendong 去博客园看该题解 题目传送门 - CodeVS1904 题目传送门 - 洛谷2764 题意概括 给出一个有向无环图,现在请你求一些路径,这些路径 ...

  6. 某种带权有向无环图(graph)的所有路径的求法

    // 讨论QQ群:135202158 最近做某个东西,最后用图实现了,这里总结一下算法. 假设有以下带权有向无环图(连通或非连通,我这里用的是非连通的): 每个节点(node)可能与其他节点有向地相连 ...

  7. 2016 湖南省省赛B题《有向无环图》

    题目链接[https://vjudge.net/problem/CSU-1804] 题意: 给出一个有向无环图,然后让你算下面的结果,count(i,j)表示i->j之间的路径条数. 题解: 根 ...

  8. UVA_1025 a Spy in the Metro 有向无环图的动态规划问题

    应当认为,有向无环图上的动态规划问题是动态规划的基本模型之一,对于某个模型,如果可以转换为某一有向无环图的最长.最短路径问题,则可以套用动态规划若干方法解决. 原题参见刘汝佳紫薯267页. 在这个题目 ...

  9. HDU 3249 Test for job （有向无环图上的最长路，DP）

     解题思路: 求有向无环图上的最长路.简单的动态规划 #include <iostream> #include <cstring> #include <cstdlib ...

随机推荐

  1. jQuery.ajax 调用 服务（.aspx，.asmx）

    方法1:Post(json)+IIS下://aspx,适用本机 $.ajax({ url: "TpgConnect_Rain/postgreService.aspx/getRainInfo& ...

  2. Atitit 乌合之众读后感attilax总结 与读后感结构规范总结

    Atitit 乌合之众读后感attilax总结 与读后感结构规范总结 1. 背景概览与鸟瞰overview 1 1.1. 社会背景 与 历史事件背景  与历史时间背景 1 1.2. 书籍简绍 2 1. ...

  3. Delphi调用java so

    package hardware.print; public class printer { static public native int Open(); } jni导出的函数是 Java_har ...

  4. [HBase Manual]CH5 HBase运行模式：单实例和分布式

    HBase运行模式:单实例和分布式 HBase运行模式:单实例和分布式 1.单实例模式 1.1 单实例在HDFS下 2.分布式 2.1 伪分布式 3完全分布式 HBase有2种运行模式,单实例和分布式 ...

  5. Variable number of arguments (Varargs)

    A parameter of a function (normally the last one) may be marked with vararg modifier: fun <T> ...

  6. Python3将ipa包中的文件按大小排序

    [本文出自天外归云的博客园] 给你个ipa包,解压前输出包大小,解压后把里面的文件按大小排序.代码如下: import os import shutil import zipfile _ipa_zip ...

  7. vim常用技巧

    # vim常用技巧 ## 行操作------------------------------ 行首 0- 行尾 $- 第一个非空字符 ^ ## 列编辑模式----------------------- ...

  8. 从零开始搭建FAQ引擎--基于ES的字面匹配

    从零开始搭建FAQ引擎--基于ES的字面匹配

  9. [Linux]Linux read/write

    Read 默认read是block模式,如果想设置非block默认,则open时候参数添加O_NONBLOCK read block模式下,并非等到Buffer满才返回,而是只要有data avaia ...

  10. Postman-REST-Client_v0.8.1之chrome插件下载

    一.前言 安装chrome浏览器postman-rest-client插件,实现基于资源RestFul的http协议的GET.POST.DELETE.PUT等方式请求调用,具体安装使用步骤如下所示 二 ...