softmax 杂谈

在多分类问题中，我们可以使用 softmax 函数，对输出的值归一化为概率值。下面举个例子：

import sys

sys.path.append("E:/zlab/")
from plotnet import plot_net, DynamicShow

num_node_list = [10, 7, 5]
figsize = (15, 6)
plot_net(num_node_list, figsize, 'net')

Press `c` to save figure to "net.svg", `Ctrl+d` to break >>
> c:\programdata\anaconda3\lib\site-packages\viznet\context.py(45)__exit__()
-> plt.savefig(self.filename, dpi=300)
(Pdb) c

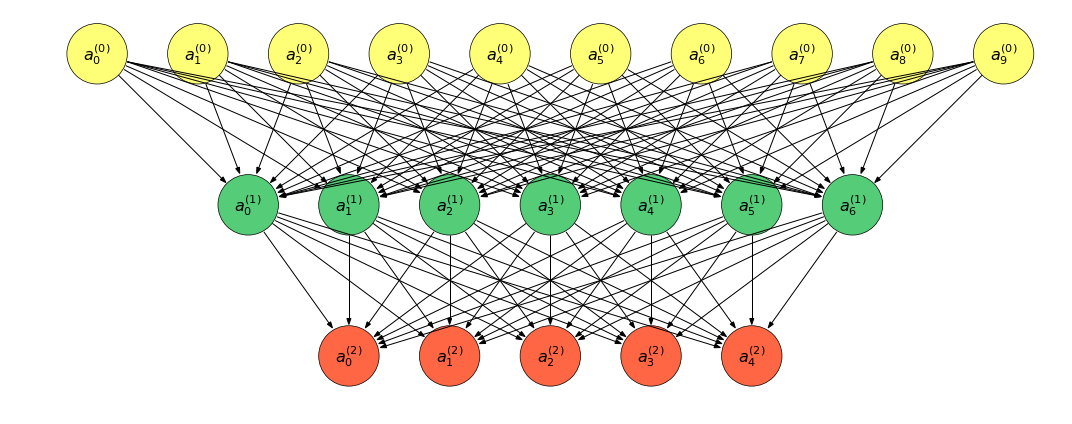
上图转换为表达式：

\[\begin{aligned}
&a^{(0)} = (a_0^{(0)}, a_1^{(0)}, \cdots, a_9^{(0)})^T\\
&a^{(1)} = (a_0^{(1)}, a_1^{(1)}, \cdots, a_6^{(1)})^T\\
&a^{(2)} = (a_0^{(2)}, a_1^{(2)}, \cdots, a_4^{(2)})^T\\
\end{aligned}
\]

对于任意的 \(0 \leq i \leq 2\), 有前向传播的表达式：

\[\begin{aligned}
&z^{(i+1)} = W^{(i)}a^{(i)} + b^{(i)}\\
&a^{(i+1)} = f^{(i+1)}(z^{(i+1)})
\end{aligned}
\]

其中，\(f^{(j)}\) 表示激活函数，除了输出层外，一般使用 ReLU 函数；\(W^{(i)}, b^{(i)}\) 为模型参数。

如若我们有 \(m\) 个样本 \(\{x^{(j)}\}_{j=1}^m\) 组成的数据集 \(D\), 称 \(X = (x^{(1)}, x^{(2)}, \cdots, x^{(m)})^T\) 为数据集 \(D\) 的设计矩阵。

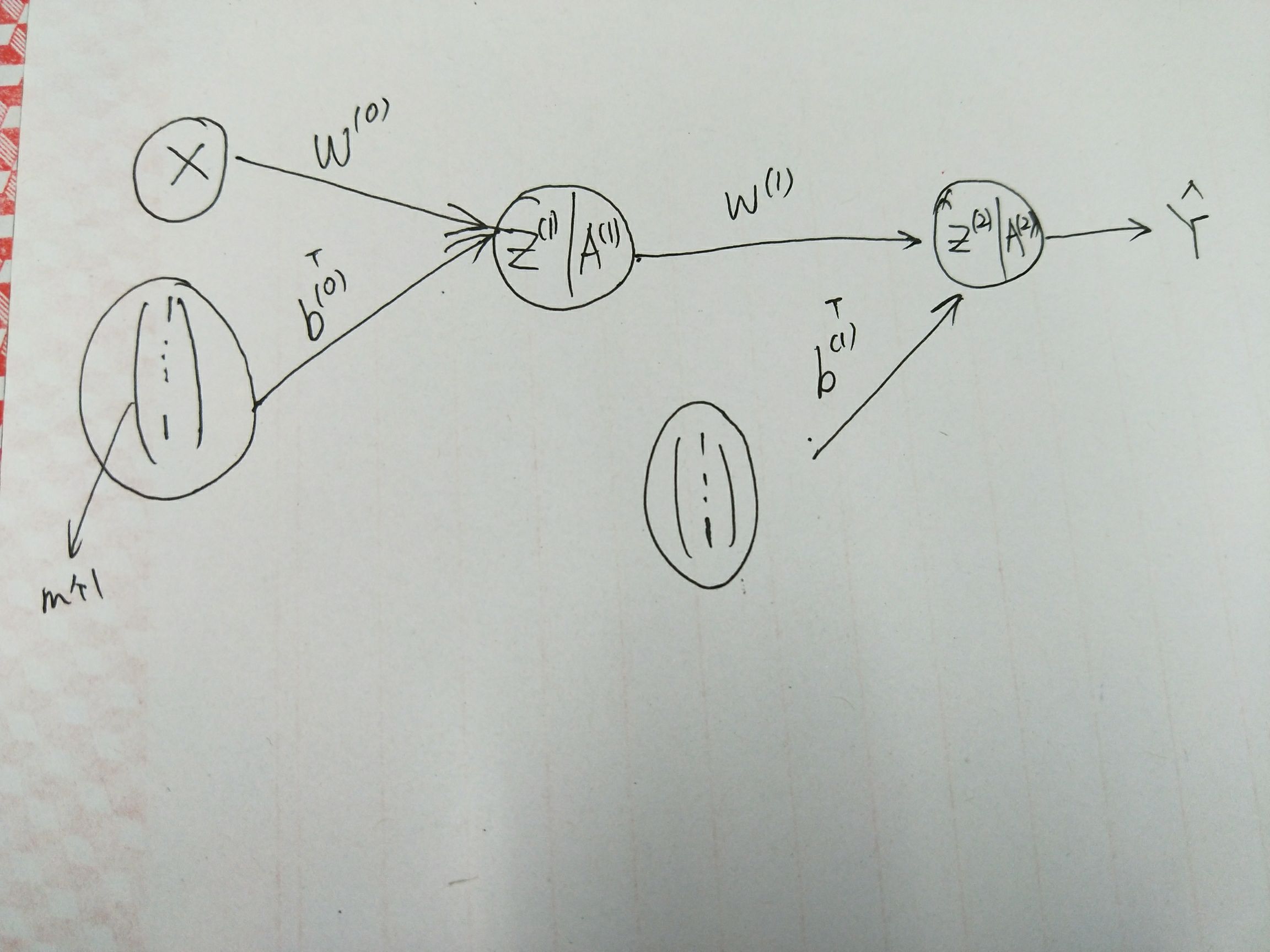
这样，前向传播可以改写为：

\[\begin{cases}
Z^{(1+i)} = Z^{(i)}W^{(0)} + (b^{(i)})^T\\
A^{(1+i)} = f^{(1+i)}(Z^{(1+i)})
\end{cases}
\]

• \(Z^{(i)} = (z_1^{(i)}, z_2^{(i)}, \cdots, z_m^{(i)})^T\), 这里对 \(z^{(i)}\) 添加下标以区别不同的样本;
• 这里对列向量 \(b^{(i)}\) 进行了 broadcast 操作;
• 且 \(Z^{(0)} = X\).

对于多分类问题，一般输出层对应的激活函数的 softmax 函数：

求解 \(A^{(2)}\):

1. 计算 \(exp = \exp(Z^{(1)})\);
2. 对 \(exp\) 按列做归一化, 便可得到 \(\text{softmax}(A^{(1)})\).

import numpy as np

def softmax(X):
    X_exp = np.exp(X)
    partition = X_exp.sum(axis=1, keepdims=True)
    return X_exp / partition  # 这里应用了广播机制。

softmax([[2, 3,4], [3, 5, 7]])

array([[0.09003057, 0.24472847, 0.66524096],
       [0.01587624, 0.11731043, 0.86681333]])

但如果输入值较大或较小时，会出现内存溢出的现象：

softmax([1000, 1000, 100])

C:\ProgramData\Anaconda3\lib\site-packages\ipykernel\__main__.py:5: RuntimeWarning: overflow encountered in exp
C:\ProgramData\Anaconda3\lib\site-packages\ipykernel\__main__.py:7: RuntimeWarning: invalid value encountered in true_divide

array([nan, nan,  0.])

softmax([-10000, -1020, 100, -70220])

array([0., 0., 1., 0.])

一种简单有效避免该问题的方法就是让 \(\exp(z_j)\) 中的 \(z_j\) 替换为 \(z_j - \max_{i} \{z_i\}\), 由于 \(\max_{i}\) 是个固定的常数，所以 \(\exp(z_j)\) 的值没有改变。但是，此时避免了溢出现象的出现。

def softmax(X):
    X = np.asanyarray(X)
    X -= X.max(axis=-1, keepdims=True)
    X_exp = np.exp(X)
    print(X_exp)
    partition = X_exp.sum(axis=-1, keepdims=True)
    return X_exp / partition  # 这里应用了广播机制。

softmax([1000, 1000, 100])

[1. 1. 0.]

array([0.5, 0.5, 0. ])

softmax([-10000, -1020, 100, -7220])

[0. 0. 1. 0.]

array([0., 0., 1., 0.])

softmax([-10000, -1020, 100, -70220])

[0. 0. 1. 0.]

array([0., 0., 1., 0.])

当然这种做法也不是最完美的，因为 softmax 函数不可能产生 0 值，但这总比出现 nan 的结果好，并且真实的结果也是非常接近 \(0\) 的。

除此之外，还有一个问题：如果我们计算 \(\log \text{softmax} (z_j)\) 时，先计算 \(\text{softmax}\) 再将其传递给 \(\log\)，会错误的得到 \(-\infty\)

np.log(softmax([-10000, -1020, 100, -70220]))

[0. 0. 1. 0.]

C:\ProgramData\Anaconda3\lib\site-packages\ipykernel\__main__.py:1: RuntimeWarning: divide by zero encountered in log
  if __name__ == '__main__':

array([-inf, -inf,   0., -inf])

最简单的处理方式是直接加一个很小的常数：

np.log(softmax([-10000, -1020, 100, -70220])+ 1e-7)

[0. 0. 1. 0.]

array([-1.61180957e+01, -1.61180957e+01,  9.99999951e-08, -1.61180957e+01])

为了解决此数值计算的不稳定，MXNet 提供了：

from mxnet.gluon import loss as gloss
loss = gloss.SoftmaxCrossEntropyLoss()

解决计算交叉熵时出现的数值不稳定的问题。

更多数据挖掘内容见：datamining