uva12558 Egyptian Fractions (HARD version)（迭代深搜）

Egyptian Fractions (HARD version)

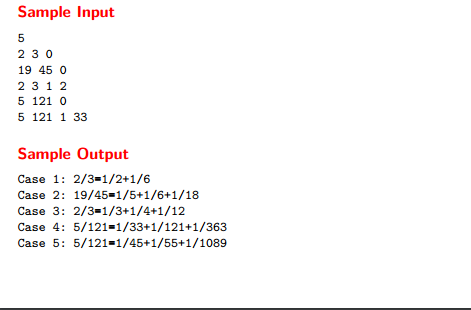
题解:迭代深搜模板题，因为最小个数，以此为乐观估价函数来迭代深搜，就可以了。

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 #include<cstdlib>
 #define LL long long
 #define N 10
 using namespace std;

 LL dep,flag,pre[N],now[N];
 bool book[];

 // 函数功能：求最大公约数
 LL gcd(LL a,LL b){return b?gcd(b,a%b):a;}

 // 函数功能：遍历第dep步的所有解
 void dfs(LL a,LL b,LL k)
 {
     if(b%a==&&b/a>now[k-]&&(b/a>||!book[b/a])) // 找到符合要求的结果
     {           /* 不要忘记判断最后的结果是否能使用，不然会WA，且要记得b/a的范围在1000以内才能判断，不然会数组越界 */
         /* 不能把book放下面判断，没有循环continue不能用，return会出错，可能没有到达dep步b%a==0，但是b/a是不能使用的 */
         now[k]=b/a;
         bool ans=;
         for(int i=k;i>=;i--)
         {
             if(now[i]<pre[i])
             {
                 ans=;
                 break;
             }
             else if(now[i]>pre[i])
                 break;
         }
         if(!flag||ans)
             memcpy(pre,now,sizeof(now));
         flag=;
         return ;
     }
     LL s=b/a;
     if(s<=now[k-]) s=now[k-]+;
     LL t=(dep-k+)*b/a;   // 迭代搜索执行到第dep步就结束了，限制上界
                           /* 之所以是这个公式是，s是使等式成立最接近的解，把s平均拆分成dep-k+1份，如果没t还小，剩下的dep-k步无论取多少都会偏小  */
     if(flag&&t>pre[dep]) t=pre[dep]-;
     for(LL i=s;i<=t;i++)
     {
         if(i<=&&book[i]) // 判断这个点能否使用，不要忘记范围，不要越界访问
             continue;
         now[k]=i;
         LL m=gcd(a*i-b,b*i);
         dfs((a*i-b)/m,(b*i)/m,k+);
     }
     return;
 }

 // 函数作用：简洁。可去掉，放在main函数中
 inline void slove(LL a,LL b)
 {
     now[]=;
     for(dep=;dep<=N;dep++)
     {
         dfs(a,b,);
         if(flag)
         {
             printf("1/%lld",pre[]);
             for(LL i=;i<=dep;i++)
                 printf("+1/%lld",pre[i]);
             printf("\n");
             return;
         }
     }
 }

 int main()
 {
     int T,cnt=;
     scanf("%d",&T);
     while(T--)
     {
         flag=;memset(book,false,sizeof(book));
         LL a,b,k,x;
         scanf("%lld %lld %lld",&a,&b,&k);
         while(k--)
         {
             scanf("%lld",&x);
             book[x]=true;
         }
         printf("Case %d: %lld/%lld=",cnt++,a,b);
         slove(a,b);
     }
 }