并查集入门（hdu1232“畅通工程”）

在学习并查集之前，首先需要明白基本的并查集可以完成的功能。并查集主要是用于处理不相交集合的合并问题。它是一种基础算法，在离散数学中，可以利用并查集求一个图的连通分支，利用其这个特性可以为我们解决一系列的问题，例如hdu1232"畅通工程"等等。在这里便利用这道题理解并查集的基本知识。

在讲解题目之前，先了解一下并查集。并查集就是将一系列的元素根据题中所给的相关关系，将它们分成一个个互不相交的集合。具体的步骤是分别找到当前的两个元素的代表元素(并查集一般是对两个元素之间的关系进行判断)（代表元素是每一个集合的象征，一个集合区别于其他集合的原因就是各自的代表元不相同）。若二者代表元素不同则说明二者之前是不同的集合，但因为有了这两个元素的关系，这两个元素所在的集合便会合并成一个集合，而之前两个元素各自集合的代表元便会合并成一个代表元，因为此时两个集合已经合并成了一个集合，而一个集合只能有一个代表元；若二者在同一个集合内，便没有了合并集合，合并代表元的步骤。在最后只需要判断有多少个代表元，便可知道有多少个不相交的集合，也就是离散数学中的多少个连通分支。看到这，零基础的可能会不太理解，没关系，通过下面的这道题来讲解。

hdu1232"畅通工程"：http://acm.hdu.edu.cn/showproblem.php?pid=1232

Problem Description

某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？

 

Input

测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2
1
这种输入也是合法的
当N为0时，输入结束，该用例不被处理。

 

Output

对每个测试用例，在1行里输出最少还需要建设的道路数目。

 

Sample Input

4 2

1 3

4 3

3 3

1 2

1 3

2 3

5 2

1 2

3 5

999 0

0

 

Sample Output

1

0

2

998

Huge input, scanf is recommended.

看到这道题求最少修建的道路，也就是求连通分支数减一，便是并查集的经典问题。

首先第一步在未输入城镇连接关系时，应将每一个城镇都看作是一个单独的集合，因为此时他们还没有建立必然关系，随着城镇之间关系的输入，逐步缩小集合数量。

for(int i=1;i<=n;i++)

    s[i]=i;

这个循环既建立了n个集合，又暗示了如何判断一个集合的代表元，那就是只有当s[i]==i时，i为代表元。

接下来随着x y的输入，意义是x y之间存在道路，xy是一个集合内的。

void merge (int x,int y)

{

    x=find(x);                                                         //找到x所在集合的 代表元，并将其值赋值给x

    y=find(y);

    s[x]=s[y];                                                          //合并xy两个集合的代表元（即便xy之前就已经是一个集合了，但是这一步也不影响）

}

int find(int x)                                                    //find函数的作用是返回传递的实参所在集合的代表元

{

    while(x!=s[x])

        x=s[x];

    return x;

}

 

经过前面的步骤这道简单题基本就可以解决了，最后只需判断还有多少代表元，即还有多少互不相交的集合，让其数量减一即为所求。

int sum=0;

for(int i=1;i<=n;i++)

    if(s[i]==i) sum++;

综上所述，这道题的AC代码如下所示：

#include<bits/stdc++.h>
#define maxn 1000+5
using namespace std;
int s[maxn]={0};
int merge(int x,int y);
int find(int x);
int main()
{
int n,m,x,y;
while(1)
{
cin>>n;
if(!n) break;
cin>>m;
for(int i=1;i<=n;i++)
s[i]=i;
for(int i=1;i<=m;i++)
{
cin>>x>>y;
merge(x,y);
}
int sum=0;
for(int i=1;i<=n;i++)
if(s[i]==i) sum++;
cout<<sum-1<<endl;
}
return 0;
}
int merge(int x,int y)
{
x=find(x);
y=find(y);
s[x]=s[y];
}
int find(int x)
{
int r=x;
while(r!=s[r])
r=s[r];
return r;
}

这样的代码在hdu上的提交显示是140ms,这样写的代码可以说是最暴力的代码，几乎没有进行优化。接下来就讲解一种优化方案，查询的优化（路径压缩），在find函数中，若要找到x的代表元r，需要一步一步的向上进行查找，虽说这样肯定可以找到，不过一旦数据量过大，极易出现查询路径过长，导致每次查询时间变长，影响查询效率。

左边的图便是没有优化前的模型，右边的图是进行查询优化的理想状态。

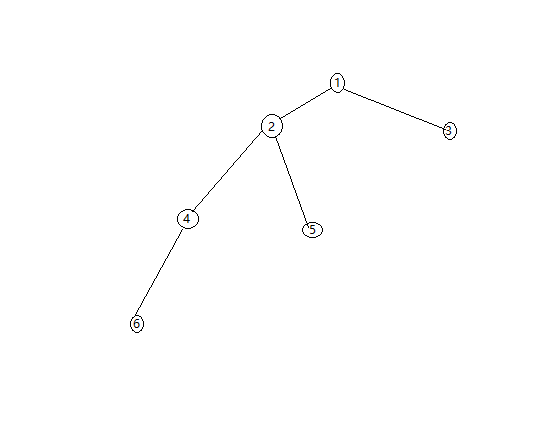
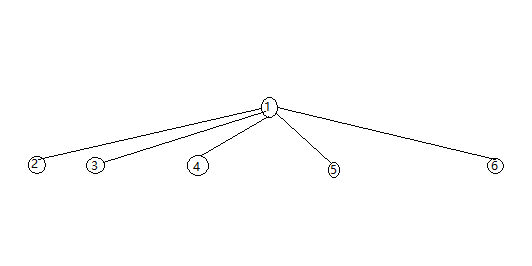
右图相比于左图只需改动find函数即可，先改动如下：

int find(int x)

{

int r=x;

while(r!=s[r])    r=s[r];

int i=x,j;

while(i!=r)

{

j=s[i];

s[i]=r;

i=j;

}

return r;

}

经过这样的路径压缩，在hdu1232上的提交，显示用时109ms,效率的提升，主要是因为进行了查询的优化。

除了查询的优化，还有合并的优化，不过我自己觉得合并的优化其实并不太重要，这个优化可以说对于用时几乎优化率很低，所以在这里只简单说一下（把高度较小的集合并到高度较高的集合上，这样可以避免树的高度无脑的增加），并写下相关代码：

#include<bits/stdc++.h>
#define maxn 1000+5
using namespace std;
int s[maxn]={0};
int height[maxn];
int merge(int x,int y);
int find(int x);
int main()
{
int n,m,x,y;
while(1)
{
cin>>n;
if(!n) break;
cin>>m;
for(int i=1;i<=n;i++)
{
s[i]=i;
height[i]=0;
}
for(int i=1;i<=m;i++)
{
cin>>x>>y;
merge(x,y);
}
int sum=0;
for(int i=1;i<=n;i++)
if(s[i]==i) sum++;
cout<<sum-1<<endl;
}
return 0;
}
int merge(int x,int y)
{
x=find(x);
y=find(y);
if(height[x]==height[y])
{
height[x]++;
s[y]=x;
}
else
{
if(height[x]<height[y]) s[x]=y;
else s[y]=x;
}
}
int find(int x)
{
int r=x;
while(r!=s[r])
r=s[r];
return r;
}

这样在hdu1232用时124ms;

不管我怎么优化，耗时一直在100ms开外，在提交列表中，有人可以15ms,31ms的通过，开始我以为是不是函数调用浪费时间，把这几个函数都写进main函数，利用for循环进行实现，不过这样看起来整个程序的条理性较低，不过幸好这道题比较简单，都写在main函数中也比较容易，但是提交之后耗时仍没什么大变化，最后再看看题发现在题后有这么一句话：Huge input, scanf is recommended.这是说这道题的输入量比较大，在scanf与cin优缺点比较中，scanf的输入较快，cin书写方便，但是做ACM，最好还是用scanf，如果最后因为输入的不同导致的超时，哭都来不及。改为scanf后，耗时15ms。两种输入将近10倍之差。（在提交的过程中，发现有时即使是同一段代码，但是耗时竟然会有微小的差异，让我至今有些不太理解）