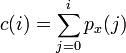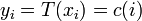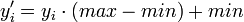数学之路-python计算实战(14)-机器视觉-图像增强(直方图均衡化)
我们来看一个灰度图像,让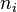 表示灰度
表示灰度 出现的次数,这样图像中灰度为
出现的次数,这样图像中灰度为 的像素的出现概率是
的像素的出现概率是
 是图像中全部的灰度数,
是图像中全部的灰度数, 是图像中全部的像素数,
是图像中全部的像素数,  实际上是图像的直方图,归一化到
实际上是图像的直方图,归一化到  。
。
把  作为相应于
作为相应于  的累计概率函数, 定义为:
的累计概率函数, 定义为:
 是图像的累计归一化直方图。
是图像的累计归一化直方图。
我们创建一个形式为  的变化,对于原始图像中的每一个值它就产生一个
的变化,对于原始图像中的每一个值它就产生一个  ,这样
,这样  的累计概率函数就能够在全部值范围内进行线性化,转换公式定义为:
的累计概率函数就能够在全部值范围内进行线性化,转换公式定义为:
注意 T 将不同的等级映射到  域。为了将这些值映射回它们最初的域,须要在结果上应用以下的简单变换:
域。为了将这些值映射回它们最初的域,须要在结果上应用以下的简单变换:
上面描写叙述了灰度图像上使用直方图均衡化的方法。可是通过将这样的方法分别用于图像RGB颜色值的红色、绿色和蓝色分量,从而也能够对彩色图像进行处理。
- Python: cv2.equalizeHist(src[, dst]) → dst
- C: void cvEqualizeHist(const CvArr* src, CvArr* dst)
-
Parameters: - src – Source 8-bit single channel image.
- dst – Destination image of the same size and type as src .
The function equalizes the histogram of the input image using the following algorithm:
Calculate the histogram
 for src .
for src .Normalize the histogram so that the sum of histogram bins is 255.
Compute the integral of the histogram:

Transform the image using
 as a look-up table:
as a look-up table: 
The algorithm normalizes the brightness and increases the contrast of the image.
# -*- coding: utf-8 -*-
#code:myhaspl@myhaspl.com
import cv2
fn="test1.jpg"
myimg=cv2.imread(fn)
img=cv2.cvtColor(myimg,cv2.COLOR_BGR2GRAY)
newimg=cv2.equalizeHist(img)
cv2.imshow('src',img)
cv2.imshow('dst',newimg)
cv2.waitKey()
cv2.destroyAllWindows()
本博客全部内容是原创,假设转载请注明来源
http://blog.csdn.net/myhaspl/
watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvbXloYXNwbA==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center" alt="" />
直方图均衡化通经常使用来添加很多图像的全局对照度,尤其是当图像的实用数据的对照度相当接近的时候。
通过这样的方法,亮度能够更好地在直方图上分布。这样就能够用于增强局部的对照度而不影响总体的对照度
本博客全部内容是原创,假设转载请注明来源
http://blog.csdn.net/myhaspl/
# -*- coding: utf-8 -*-
#code:myhaspl@myhaspl.com
#直方图均衡化
import cv2
import numpy as np
fn="test5.jpg"
myimg=cv2.imread(fn)
img=cv2.cvtColor(myimg,cv2.COLOR_BGR2GRAY)
h=img.shape[0]
w=img.shape[1]
newimg=np.zeros((h,w),np.uint8)
scount=0.0
#原始图像灰度级
scol={}
#目标图像灰度级
dcol={}
#原始图像频度
Ps={}
#累计概率
Cs={} #统计原始图像灰度级
for m in xrange(h):
for n in xrange(w):
scol[img[m,n]]=scol.setdefault(img[m,n],0)+1
scount+=1

数学之路-python计算实战(14)-机器视觉-图像增强(直方图均衡化)的更多相关文章
- 数学之路-python计算实战(13)-机器视觉-图像增强
指数变换的基本表达式为:y=bc(x-a)-1 当中參数b.c控制曲线的变换形状,參数a控制曲线的位置. 指数变换的作用是扩展图像的高灰度级.压缩低灰度级.能够用于亮度过高的图像 本博客全部内容是原创 ...
- 数学之路-python计算实战(21)-机器视觉-拉普拉斯线性滤波
拉普拉斯线性滤波,.边缘检測 . When ksize == 1 , the Laplacian is computed by filtering the image with the follow ...
- 数学之路-python计算实战(17)-机器视觉-滤波去噪(中值滤波)
Blurs an image using the median filter. C++: void medianBlur(InputArray src, OutputArray dst, int ks ...
- 数学之路-python计算实战(20)-机器视觉-拉普拉斯算子卷积滤波
拉普拉斯算子进行二维卷积计算,线性锐化滤波 # -*- coding: utf-8 -*- #线性锐化滤波-拉普拉斯算子进行二维卷积计算 #code:myhaspl@myhaspl.com impor ...
- 数学之路-python计算实战(15)-机器视觉-滤波去噪(归一化块滤波)
# -*- coding: utf-8 -*- #code:myhaspl@myhaspl.com #归一化块滤波 import cv2 import numpy as np fn="tes ...
- 数学之路-python计算实战(19)-机器视觉-卷积滤波
filter2D Convolves an image with the kernel. C++: void filter2D(InputArray src, OutputArray dst, int ...
- 数学之路-python计算实战(9)-机器视觉-图像插值仿射
插值 Python: cv2.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]]) → dst interpolation – interpol ...
- 数学之路-python计算实战(16)-机器视觉-滤波去噪(邻域平均法滤波)
# -*- coding: utf-8 -*- #code:myhaspl@myhaspl.com #邻域平均法滤波,半径为2 import cv2 import numpy as np fn=&qu ...
- 数学之路-python计算实战(18)-机器视觉-滤波去噪(双边滤波与高斯滤波 )
高斯滤波就是对整幅图像进行加权平均的过程.每个像素点的值,都由其本身和邻域内的其它像素值经过加权平均后得到.高斯滤波的详细操作是:用一个模板(或称卷积.掩模)扫描图像中的每个像素.用模板确定的邻域内像 ...
随机推荐
- Joel在耶鲁大学的演讲
Joel Spolsky是一个美国的软件工程师,他的网络日志"Joel谈软件"(Joel on Software)非常有名,读者人数可以排进全世界前100名. 上个月28号,他回到 ...
- 异常:cvc-complex-type.2.4.a: Invalid content was found starting with element
web.xml 出现cvc-complex-type.2.4.a: Invalid content was found starting with element <web-app xmlns= ...
- HTML解决div里面img的缝隙问题
图片IMG与容器下边界之间有空隙怎么办?这里介绍3中简单的解决方法. 第一,给图片img标签display:block. img{display:block} 第二,定义容器里的字体大小为0. div ...
- 解决Sublime Text3莫名的中文乱码问题
有好几回用Sublime Text3写着中英混杂的文字的时候,会突然就弹出警告说什么编码不行,然后点击确定后,原来的中文全都乱码了: 然后即使按ctrl+z撤回也没用,重新打开也没用,用记事本的转换a ...
- cocos2dx工程
1. create-android-project.sh 进入 pro.android/ ln -s ../Resources ./Resources
- GROUPING SETS、ROLLUP、CUBE
大家对GROUP BY应该比较熟悉,如果你感觉自己并不完全理解GROUP BY,那么本文不适合你.还记得当初学习SQL的时候,总是理解不了GROUP BY的作用,经过好长时间才终于明白GROUP BY ...
- window下nodejs安装指南
相信对于很多关注javascript发展的同学来说,nodejs已经不是一个陌生的词眼.有关nodejs的相关资料网上已经铺天盖地.由于它的高并发特性,造就了其特殊的应用地位. 国内目前关注最高,维护 ...
- 虽然net人
http://v.qq.com/boke/page/c/h/0/c01173tzeh0.html http://v.qq.com/boke/page/r/7/x/r0117l07r7x.html ht ...
- 基于visual Studio2013解决C语言竞赛题之0403字符统计
题目 解决代码及点评 这道题的目标是锻炼while循环,while循环的语法是 while(循环条件) { 循环体; } 每次进入循环体之前,先判断循环条件是否满足,如果不满足,执行序列就 ...
- git 使用过程(一、准备工作)
没有多余的废话,只是纯粹的捞干的记录下一自己使用Git的过程.(正在学习中,也是刚接触,记录过程可能有点乱.等熟悉之后在重新整理一下) 一.先下载git客户端 网址:http://msysgit.gi ...