Incircle and Circumcircle（二分+几何）浙大月赛zoj3806（详解版）图

Incircle and Circumcircle

---

Time Limit: 2 Seconds Memory Limit: 65536 KB Special Judge

---

A triangle is one the basic shapes in geometry. It's a polygon with three vertices and three sides which are line segments. A triangle with vertices A, B, C is denoted ΔABC. And its three sides, BC, CA, AB are often denoted a, b and c.

The incircle of a triangle is the largest circle contained in the triangle, it is tangent to the three sides. The center of the incircle is called the triangle's incenter and the radius of the incircle is called inradius, which is denoted r.

The circumcircle of a triangle is the circle which passes through all its three vertices. The center of the this circle is called circumcenter and its radius is called circumradius, which is denoted R.

It's very easy to calculate r and R after knowing a, b and c. Now you are given r and R, can you calculate a valid triple (a, b, c)?

Input

There are multiple cases. Each case has two positive integers r and R in one line. (r and R are less than 10⁵)

Ouput

For each case, print three floating numbers a, b and c in one line if it's possible to get r and R. If there are no possible tuples, print "NO Solution!".

The judge program uses your a, b and c to calculate the inradius and circumradius. Only the relative error of your inradius and circumradius less than 10^-8 will be accepted.

Sample Input

1 2
2 5
9 9

Sample Ouput

3.464101615137754587 3.464101615137754587 3.464101615137754587
6 8 10
NO Solution!

题目大意：给你一个三角形的内切圆半径跟外接圆半径，求解出符合条件的三角形，输出三角形的三条边的长度，如果没有符合条件的三角形，输出“NO Solution!”。

解题思路：这个题是SP,既是因为情况不唯一，而且还有精度的误差。

首先能够想到的就是NO Solution!的情况，即当内切圆半径等于1/2外接圆半径时，此时内切圆最大，而三角形为等边三角形，如图。

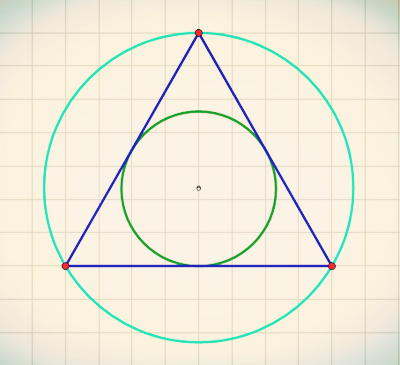
其次要解决的就是怎么构造三角形的问题，因为解不唯一，所以只要列举出一种解就OK，于是就很容易的想到构造等腰三角形，在最大与最小之间二分等腰三角形的底边长度，解三角形得到答案，如图。

思路就是二分，不明白的看下面的图；

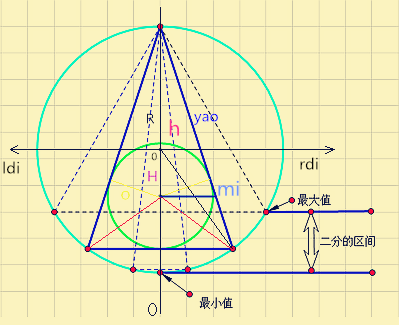
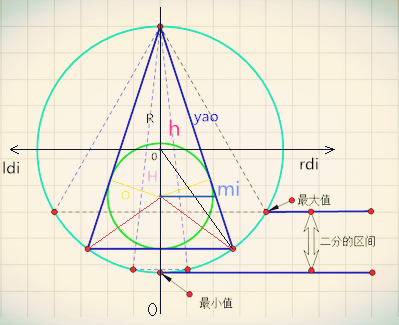
ps：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=5338

浙大月赛ZOJ Monthly, August 2014其他题

http://www.cnblogs.com/yuyixingkong/p/3935199.html

#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int main()
{
    double r,R;
    double ldi,rdi,mi;//左，右，中
    double H,h,yao,o;//H：外心到等腰三角形底边的距离；h：等腰三角形的高；yao：表示腰长；o：内心半径
    double eps=1e-;
    while(~scanf("%lf%lf",&r,&R))
    {
        if(R>*r)
        {
            printf("NO Solution!\n");
            continue;
        }
        ldi=;
        rdi=R*sqrt()/;//最大等边三角形；所以区间长度最长是
        while(rdi-ldi>eps)
        {
            mi=(rdi+ldi)/;
            H=sqrt(R*R-mi*mi);
            h=H+R;
            yao=sqrt(h*h+mi*mi);
            o=(mi*h)/(yao+mi);//等腰三角形同面积法
            if(o<r)
                ldi=mi;
            else
                rdi=mi;
        }
        mi=(rdi+ldi)/;
        H=sqrt(R*R-mi*mi);
        h=H+R;
        yao=sqrt(h*h+mi*mi);
        o=(mi*h)/(yao+mi);
        printf("%.18f %.18f %.18f\n",mi*,yao,yao);
    }
    return ;
}